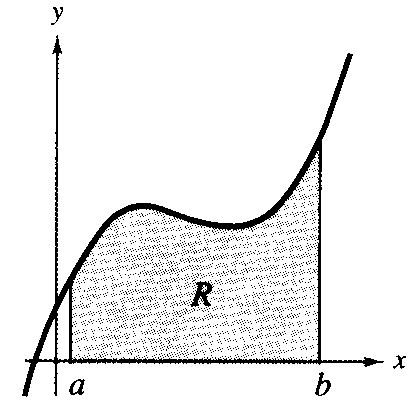
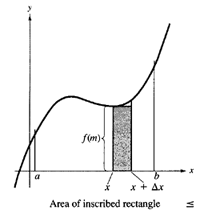
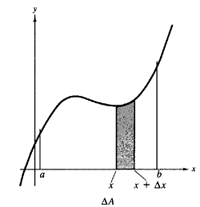
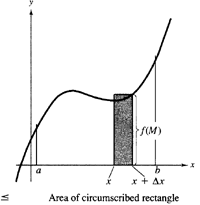
| Our problem here is to develop a way to calculate the area of a plane region R, bounded by the x-axis, the lines x = a and x = b, and the graph of a nonnegative continuous function f, as shown in the next Figure. |
 |
|
|
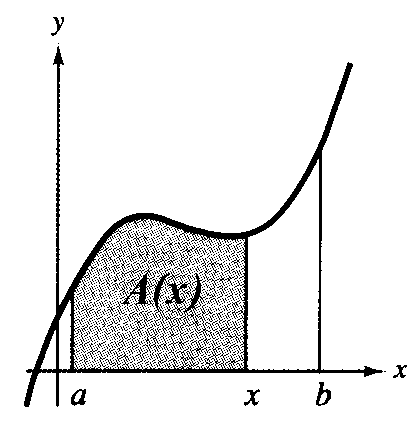 |
|
|
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
f(x) = A' (x)
|
|
A (x) = F(x) + C
|
|
A(b) = F(b) + C = F(b) -F(a)
|
|
|
|
Fundamental Theorem of Calculus
|
| If a function f is nonnegative and continuous on the closed interval [a,b] then |
|
|
| where F is any function such that F ' (x) = f (x) for all x in [a,b]. |