Particular Solution

We have already seen that the equation y = ∫ f ( x ) d x has many solutions, each differing from the others by a constant. This means that the graphs of any two antiderivatives of f are vertical translations of each other. For example, the next figure shows the graph of several antiderivatives of the form

y = ∫ ( 3 x 2 - 1 ) d x = x 3 - x + C

for various integer values of C. Each of these antiderivatives is a solution of

d y d x = 3 x 2 - 1

In many applications of integrations, we are given enogh information to determine a particular solution.
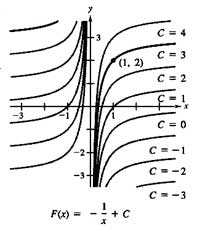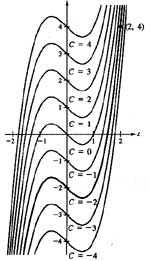
To do this, we need only know the value of F(x) for one value of s.
This information is called an initial condition.
For example, in the left hand-side figure, there is only curve that passes through the point (2,4). To find this particular curve, we use the following information.

F ( x ) = x 3 - x + C
	General solution
F(2) = 4	Initial condition

By using the initial condition in the general solution, we determine that F(2) = 8 - 2 + C = 4, which implies that C = -2.
Thus, we obtain

F ( x ) = x 3 - x - 2

Particular solution

EXAMPLE 1
Find the general solution of the equation

F ′ ( x ) = 1 x 2

and find the particular solution that satisfies the initial condition
F(1) = 2.

SOLUTION
To find the general solution, we integrate as follows.

	F(x) =	∫ 1 x 2 d x = ∫ x - 2 d x =
		= x - 1 - 1 + C = - 1 x + C

Now, since F(1) = 2 , we write

F ( 1 ) = - 1 1 + C = 2

which implies that C = 3. Thus, the particular solution is

F ( x ) = - 1 x + 3