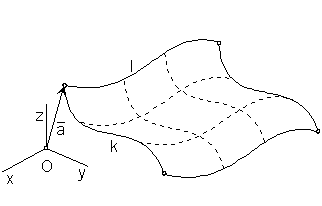
Translation surface can be created from the curve segment kTRANSLATION SURFACES
Translation surface can be created from the curve segment k
Synthetic representation: (k, TP(v))
Analytic representation:
r(u) = (x(u), y(u), z(u), 1), u Î < 0, 1 >
generating principle - class of translations determined by the curve segment h
r*(v)=(x*(v), y*(v), z*(v), 1),
v Î < 0, 1 >,
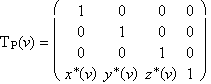
modelled figure - translation surface patch
p(u, v) = r(u) . TP(v) = (x(u) + x*(v), y(u) + y*(v), z(u) + z*(v), 1), (u, v) Î < 0, 1 >2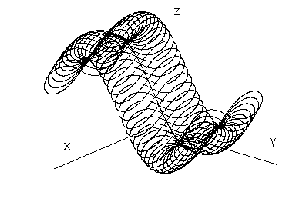
Obr. 4.37
Translation surface, created by a translation movement of the Lemniscate of Bernoulli on a sinusoidal segment is presented in the Obr. 4.37.
Special types of translation surface can be created from special curve segments k, h.
If h (trajectory of the movement) is a line segment, a patch of the cylindrical surface can be created,
or a patch of the prismatic surface.
Provided k and h are plane curve segments
located in one plane, a part of the plane can be determined.
Let the translation determined by the vector a = (m, n, l, 0) be given,
then r*(v) = (mv, nv, lv, 1), v Î < 0, 1 >.
If k is a plane curve segment, k 
a and vector a is the direction vector in the plane
a,
a surface patch can be created, which is a part of the plane
a (obr. 4.14).
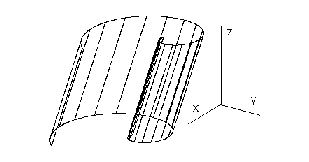
Obr. 4.14 Obr. 4.15
If the curve segment k is a circle in the plane a and vector a is not the direction vector
in the plane a, a patch of the circular cylindrical surface can be created,
for the direction a ^ a a patch of the cylindrical surface of revolution.
Illustration of a cylidrical surface patch with the basic figure in the Archimedean spiral segment is in the Obr. 4.15.
If k is a polygon and vector a is not parallel to any of the polygon sides,
the modelled surface is a patch of the prismatic surface with edges in the direction of the vector a
(surface created from planar patches).