Matrices of Projection Methods


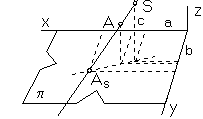
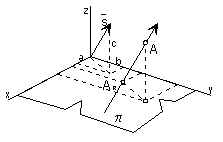
Central Projection

Centre of projection S = (a, b, c, 1), for c 0, ( or b 0) is a real point in the space ,
not located in the image plane - p = xy ( or n = xz ) .
View of an arbitrary point A in the space , A S is the point AS in the image plane,
which is the intersection point of the projecting line sA = AS passing through the point A
and the centre of projection S with the image plane

AS = sA Ç p ( or AS = sA Ç n )

Distance of the centre of projection to the image plane is d = | Sp | = c ( or d = | Sn | = b ) .

Matrix of the central projection to the ground image plane p = xy

   x´ = cx - az
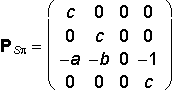
y´ = cy - bz
z´ = 0
h´ = -z + c

AS = A . PSp =

Matrix of the central projection to the frontal image plane n = xz

   x´ = bx - ay
y´ = 0
z´ = -cy + bz
h´ = -y + b

AS = A . PSn =

Centre of projection S has no view.



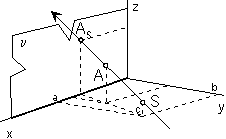
Linear perspective

Centre of projection S = (0, 0, -d, 1), distance d = 30cm is the distance of the eye to the image plane.

Matrix of the linear perspective to the ground image plane p = xy



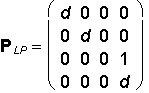
Stereoscopic projection with two centres

Centres of projection 1S = (a, b, -d, 1), 2S = (-a, b, -d, 1),
distance of the eye to the image plane d = 30cm,
distance of centres |1S 2S | = 2b = 6,5cm is the average distance of eyes

          



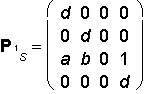
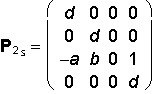
Parallel Projection

Direction of projection s - a pencil of lines in the space in the same direction, sharing a commmon ideal point with the line s,
determined by the direction vector s = (a, b, c, 0), c 0, ( or b 0 ),
intersects image plane p ( or n ) in the real point.
View of an arbitrary point A in the space is the point AP Î p ( or AP Î n ),
which is the intersection point of the line sA, A Î sA in the direction s passing through the point A with the image plane

AP = sA Ç p ( or AP = sA Ç n ) .

Matrix of the parallel projection to the ground image plane p = xy

   x´ = cx - az
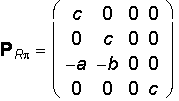
y´ = cy - bz
z´ = 0
h´ = c

AR = A . PRp =

Matrix of the parallel projection to the frontal image plane n = xz

   x´ = bx - ay
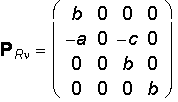
y´ = 0
z´ = -cy + bz
h´ = b

AR = A . PRn =



Orthographic projection to plane p = xy is represented by the matrix

P

with two elective angles the azimuth a and the elevation e from the interval <-360°, 360°>.


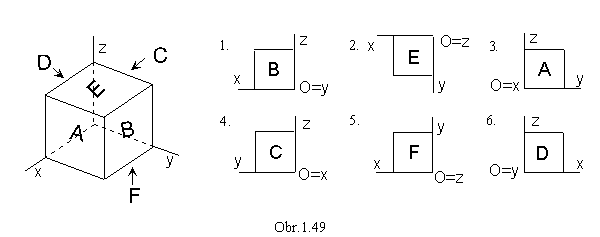
 Choosing the azimuth a and the elevation e we can obtain (obr.1.49):
1. a = e = 0°                         front view (from the front)
2. a = 0°, e = 90°                 ground view (from the top)
3. a = 90°, e = 0°                 side view (from the left side)
4. a = -90°, e = 0°                side view (from the right side)
5. a = 0°, e e = -90°             bottom view (from the bottom)
6. a = 180°, e = 90°             back view( from the backward)
7. a = ±45°, e = ±45°           isometry (obr. 1.47a)
8. a = 45°, e 0°, ±45°, ±90°, ±135°, ±180° , ±225° , ±270° , ±315°, ±360°    dimetry (obr. 1.47b)
9. a , e 0°, ±45°, ±90°, ±135°, ±180° , ±225° , ±270° , ±315°, ±360°              trimetry (obr. 1.47c)



Monge Method (Multiview Orthographic Drawing)


GROUND VIEWFRONT VIEWSIDE VIEW


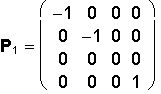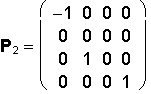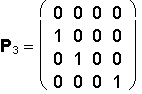Orthogonal Axonometry ( a, e 0°, ±90°, ±180°, ±270°, ±360° )


AXONOMETRIC VIEWAXON. GROUND VIEW
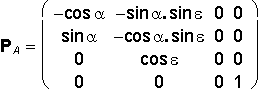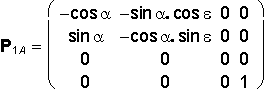AXON. FRONT VIEWAXON. SIDE VIEW
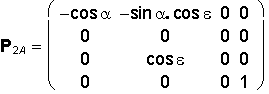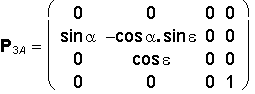