Pyramidal (prismatic) surface is determined by the basic polygon (mostly a closed planar n-gon) and main vertex, which is a real point V (an ideal point V, direction of all surface lines).
View of the surface can be determined by views of the basic n-gon (on obr. 2.62 it is located in the ground plane) and views of line segments in the surface edges.
Let the ground view of the point L on the surface be given. Line h located on the surface is passing through the point L. Ground view of the line is passing through the point ground view L₁.
By means of the intersection points on the sides of the basic n-gon, the front views of a pair of lines located on the surface and mapped to the same ground view h₁ passing through L₁ can be found.
On front views of lines h and h´, the front views of points L and L´ are located, while their ground views coincide in L₁.
Axonometric views of points L a L´ can be determined from axonometric ground views and axonometric front views.
Tangent plane to the pyramidal (prismatic) surface in the point L not located on the edge coincides with the surface face, in which the point is located, normal n is perpendicular tot the tangent plane.

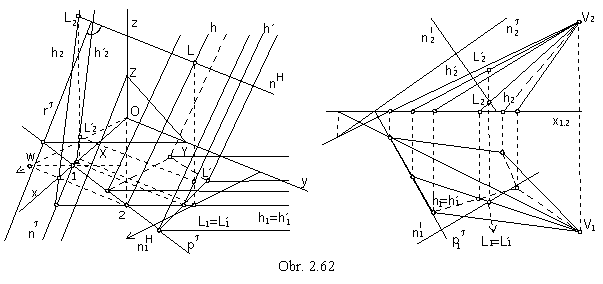
Line r^t is the axonometric trace of the tangent plane t, obr. 2.62 left.

Plane passing through the ideal point V of the prismatic surface H is the direction plane s (in the direction of the surface edges). Direction plane s, sharing one real point with the surface H, intersects the surface in:

Plane a, in a general position with respect to the prismatic surface, intersets the surface in the polygon with edges in the intersection points of the surface edges and the intersection plane. Sides of the intersection polygon are intersection line segment of the surface faces and the intersection plane.

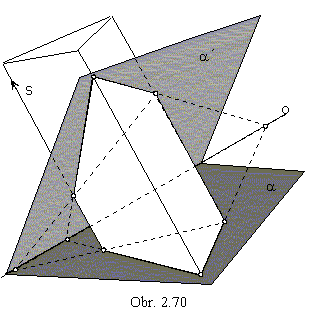Let a and a´ be not the direction planes of the prismatic surface.
Intersections of the prismatic surface and planes a and a´
are related in the axial affinity correspondence.
Axis of affinity is the intersection line of the two planes a, a´.
Direction of affinity is determined by the surface edges,
any edge intersects the planes a and a´ in the vertices of the intersections, which form the pairs of corresponding points in the axial affinity (obr. 2.70).
Parallel views of both intersections to the arbitrary image plane in the direction not parallel to any of the planes a, a´ nor to the direction of the surface edges, are two polygons related in the axial affinity correspondence.
Axis of affinity is the view of the intersection line of planes a and a´ , and direction is determined by views of surface edges.
Views of vertices of polygons in which planes a and a´ intersect the prismatic surface are pairs of correspondinf points in the created axial affinity.
Basic polygon of the prismatic surface is usually its intersection by one of the image planes and intersection by the plane a is therefore the affine image of ther basic figure.

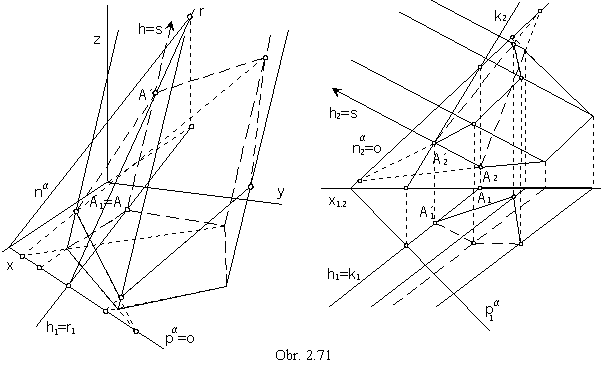
In the obr. 2.71 an oblique prismatic surface with the basic pentagon in the ground plane intersected by the plane is mapped in the Monge method,
planar intersection of the prismatic surface with four edges and the basic polygon in frontal plane is mapped in the axial affinity.
Intersection plane a is determined by traces. Intersection polygon can be found by means of axial affinity with the axis in the trace of the intersection plane and direction in the surface edges. Corresponing pair of points A, A´ are intersection points of the edge h and the image plane and intersection plane.

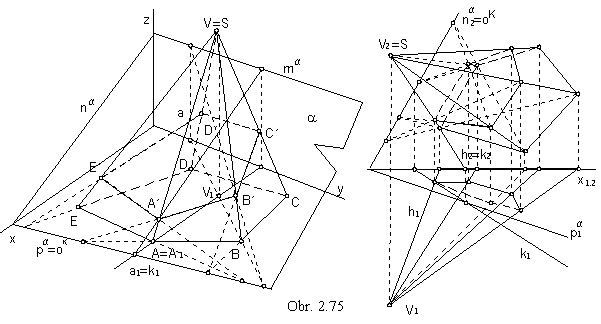
Planar intersections of pyramidal surfaces

Plane passing through the vertex V of the pyramidal surface I is the vertex plane.
Vertex plane, sharing two different points with the surface intersects surface in:

Plane a, which is not the vertex plane of the surface I, intersects the surface in the polygon with vertices in the intersection points of the surface edges and the intersection plane. Sides of the polygon are intersection line segments of the surface I faces with the intersection plane.

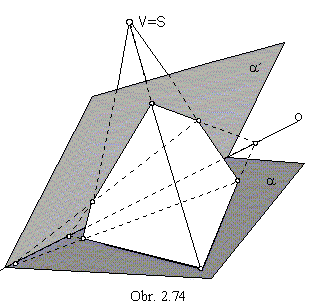Let a a a´ be not the vertex planes of the pyramidal surface.
Intersections of the surface by planes a and a´ are related in the central collineation correspondence.
Axis of collineation is the intersection line of the planes a and a´.
Centre of collineation is the vertex of the surface, edges intersect planes a and a´ in vertices of the intersection polygon, and they are pairs of corresponding points in the central collineation (obr. 2.74).
Parallel view of both intersections to an arbitrary image plane in the direction not parallel to any of the planes a and a´ are two polygons related in the central collineation.
Axis of this central collineation is the view of the intersection line of planes a and a´ and centre is the view of the pyramidal surface vertex.
Views of the vertices of intersection polygons in planes a a a´ are pairs of corresponding points.
Basic figure of the pyramidal surface is the planar intersection (usually located in one image plane), therefore the intersection of the pyramidal surface by the plane a is the collinear image of the basic figure.
In the obr. 2.75 intersection of a pyramidal surface is illustrated in both projection methods.