Intersection points of lines and surfaces

Superposition of lines and surface can be determined by and algorithm in three steps.
Let F be a surface, which line a intersects in a set of points.

If M in an empty set, line has no common points with the surface.
Line is tangent to the surface in the unique one point of the set M, if this is the case.
All points in the set M are intersection points of the line and the surface.
The maximal possible number of intersection points of a line and a surface is the degree of the surface.
With respect to the steps 2 and 3, we can decide on the choice of the arbitrary plane a in the step 1 so that the solution will be easy and reasonably accurate.
One of the strategies is to choose the projecting plane of the line a.
Intersection k is then mapped as a line segment in one view ,
while in the other one the intersection points of the line and the intersection figure can be determined.
The problem cannot be solved always in this way (intersection figure can be very complicated, a hyperbola, or so).
Other strategy is to choose the plane a in a special position with respect to the surface F, in order to receive an easy intersection figure, a line, a circle, or so.

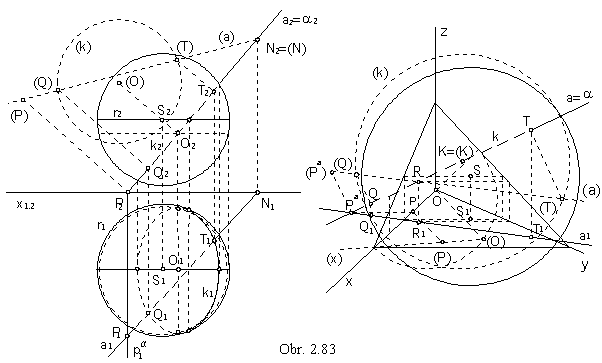
Any planea intersects sphere in a circle.
Intersection by a projecting plane of the line a is mapped in one view as a line segment.
In the obr. 2.83, the chosen plane a is the projecting plane of the line a perpendicular to the frontal plane in the Monge method, front view of the intersection circle appears as a line segment, ground view as an ellipse.
Common points Q, T of the line a and the circle k (in the view of the line a₁ an ellipse k₁) can be determined by lowering of ther plane a to the frontal image plane.
Visibility of the line with respect to the sphere is determined by the visibility of the intersection circle k.
In the orthogonal axonometry, the plane a is perpendicular to the axonometric image plane passing through the centre S of the sphere.
Lowering the plane a to the axonometric image plane r will reveal the superposition of the intersection circle k
(in axonometric view appearing as a line segment, centre K is located in the image plane r) and the line a.
Lowered position (a) of the line is determined by axonometric trace R=(R) =aÇr and lowered position (P_a) of the trace in ground plane .
Point P_a is in the same distance from the axonometric image plane as the point P located on the coordinate axis x.
This distance can be determined bu lowering the projecting plane of the coordinate axis x. | Pr | = | P(P) | = | P_a(P_a) | = | P_a r |

Line and prismatic or cylindrical surface

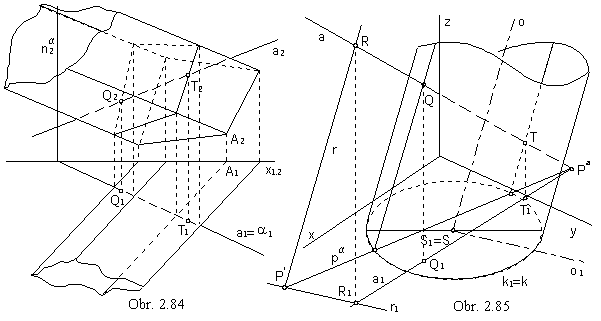
Intersection plane a parallel to the edges on the prismatic surface, or to the lines on the cylindrical surface intersects surfaces in two lines (tangent lines is tangent in one line).
Intersection points of these lines and the line a are intersection points of the line and the surface.
In the case of prismatic surfaces, it is also suitable to choose the plane a in the projecting plane of the line a (obr. 2.84).
In the case of cylindrical surfaces (obr. 2.85), the plane a is parallel to the surface axis (projecting plane can intersect the cylindrical surface in the ellipse).
In addition to the line a, line priamku r parallel to the cylindrical surface axis must be determined in the plane a, intersecting the given line a in an arbitrarily chosen point R.

R Î a, r ' R, r || o, a = a ´ r

Line and pyramidal or conical surface

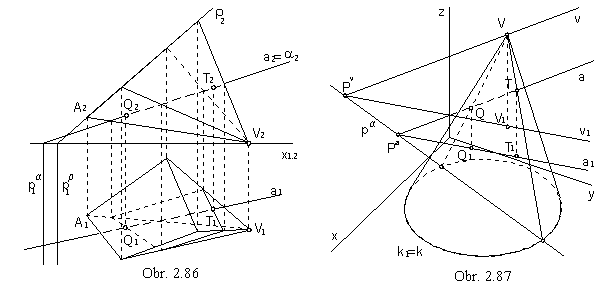
Intersection plane a passing through the vertex of the pyramidal or conical surface intersects surface in two lines (tangent plane is tangent in one line).
Given line a intersects these lines in its common points with the surface.
In the case of pyramidal surfaces, it is also suitable to choose the plane a in the projecting plane of the line a (obr. 2.86).
In the case of conical surface, where the intersection can be a conic section, the plane a is always the vertex plane, a = aV.
Additional line in the plane a is passing through the vertex V and is parallel to (obr. 2.87), or intersecting the given line a .