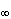Základy premietania

Špeciálne zobrazenie priestoru na zvolenú rovinu - nákresňu nazývame premietanie.
Poznáme dva základné druhy premietania, stredové a rovnobežné.

Stredové premietanie

Zvolený je vlastný bod S ∈ E3 (stred premietania), ktorý neleží v nákresni - zvolenej rovine π (priemetňa).
Obrazom ľubovoľného bodu 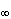A ∈ E3, A S je bod AS ∈ π, ktorý je priesečníkom priamky sA = AS (premietacia priamka),
prechádzajúcej bodom A a stredom premietania S s priemetňou, AS = sA ∩ π (obr. 1.29).
Vzdialenosť stredu premietania od priemetne nazývame dištancia

| S π | = d.

Stredu premietania nie je priradený žiadny obraz, nemá priemet.

Rovnobežné premietanie

Daný je smer s (smer premietania) - osnova priamok priestoru E3 majúcich s priamkou s spoločný nevlastný bod.
Smer s pretína nákresňu - zvolenú rovinu π (priemetňa), vo vlastnom bode.
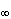Obrazom ľubovoľného bodu A ∈ E3 je bod AP ∈ π, ktorý je priesečníkom priemetne s priamkou sA, A ∈ sA zo smeru s (premietacia priamka), prechádzajúcej bodom A, AP = sA ∩ π (obr. 1.30).

Rovnobežné premietanie je špeciálnym prípadom stredového, keď stred S je nevlastným bodom priestoru E3.

Stredové ani rovnobežné premietanie nie je bijektívnym zobrazením priestoru 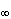E3 na rovinu.
Všetky body priemetne sú pri oboch premietaniach samodružné.
Všetky body každej premietacej priamky sa zobrazia do toho istého bodu, priesečníka s priemetňou.

Priemetom geometrického útvaru U je útvar, ktorý získame ako množinu priemetov všetkých bodov útvaru U.
Priemetom priamky, ktorá nie je premietacou priamkou, je priamka (obr. 1.31).
Priemetom premietacej priamky je bod.
Samodružný priesečník priamky s priemetňou nazývame stopník priamky.
Množina všetkých premietacích priamok bodov priamky vytvára premietaciu rovinu priamky.
Priemet priamky je priesečnica premietacej roviny priamky s priemetňou.

Priemetom roviny, ktorá nie je premietacou rovinou, je celá priemetňa. Priemetom premietacej roviny je priamka.
Priesečnicu roviny s priemetňou nazývame stopa roviny. Stopa roviny je množina stopníkov všetkých priamok roviny.
Každú priamku roviny, ktorá má so stopou roviny spoločný nevlastný bod, nazývame hlavná priamka roviny (má nevlastný stopník).
Priemetom hlavnej priamky roviny je priamka rovnobežná so stopou roviny (obr. 1.32).
Každá priamka roviny kolmá na stopu roviny (a na všetky hlavné priamky) sa nazýva spádová priamka roviny.
Ostrý uhol j, ktorý zviera spádová priamka s priemetňou je uhol, ktorý zviera rovina s priemetňou. Nazývame ho spád roviny.

Rovnobežné (stredové) premietanie je afinným (kolineárnym) zobrazením priestoru na rovinu.

Vlastnosti rovnobežného premietania:

1. Priemetom útvaru U, ktorý leží v rovine rovnobežnej s priemetňou, je útvar zhodný s útvarom U.

2. Rovnobežnosť (spoločný nevlastný bod) je invariantom rovnobežného premietania.
Rovnobežné priamky nepatriace smeru premietania majú rovnobežné priemety.
Rovnobežné roviny majú rovnobežné stopy a priemety hlavných priamok.

3. Zachováva sa deliaci pomer bodov na priamke, λ (ABC) = λ (A1 B1 C1).
Stred útvaru sa premieta do stredu priemetu útvaru (obr. 1.33).

Kolmé premietanie je také rovnobežné premietanie, pri ktorom sú všetky premietacie priamky smeru s kolmé na priemetňu.
Pre kolmé premietanie platia okrem vlastností rovnobežného premietania 1. - 3. ešte niektoré ďalšie:

4. Nech AB je úsečka na priamke a, ktorá zviera s priemetňou π uhol φ .
Pre kolmý priemet A1B1

| A1 B1 | = | AB | cos φ

Dĺžka kolmého priemetu úsečky je menšia (pre φ ∈ ( 0°, 90° ), pre φ = 90° je A1 = B1, obr. 1.33),
alebo sa rovná (pre φ = 0°) dĺžke danej úsečky (obr. 1.34, | A1 V1 | = | AV | ).

5. Pravý uhol sa premieta ako pravý, ak je aspoň jedno jeho rameno rovnobežné s priemetňou a žiadne nie je kolmé na priemetňu (obr. 1.34).
Ak rovina a nie je kolmá na priemetňu, spádové priamky roviny a sa kolmo premietajú ako kolmice na stopu (a priemety hlavných priamok) roviny a.
Kolmý priemet kolmice na rovinu je kolmý na stopu (a priemety hlavných priamok) roviny a (obr. 1.35).

Úloha zobrazenia - premietania trojrozmerných objektov na rovinu vznikla z praktických potrieb človeka a má veľký význam v mnohých oblastiach.
Pre technika však nestačí objekt len premietnuť, ale potrebuje z príslušného nákresu - obrazu objektu zistiť niektoré jeho vlastnosti, prípadne objekt jednoznačne zrekonštruovať.
Táto úloha sa realizuje pomocou rôznych zobrazovacích metód.

Zobrazovacia metóda je bijektívne (prosté a na) zobrazenie bodov priestoru na rovinu.
Najznámejšie zobrazovacie metódy sú: kótované premietanie, pravouhlé premietanie na dve navzájom kolmé priemetne (Mongeova projekcia),
kolmá a šikmá axonometria, stredové premietanie a lineárna perspektíva, dvojstredové (stereoskopické) premietanie.
Voľba vhodnej zobrazovacej metódy závisí od toho, akému účelu má príslušný nákres slúžiť.
V umení, architektúre a staviteľstve sa používa lineárna perspektíva, Mongeova projekcia, axonometria, príp. kótované premietanie.
V strojárenstve sú najvhodnejšie Mongeova projekcia a axonometria.
Práca inžinierov konštruktérov, ktorí navrhujú nové stroje, prístroje či súčiastky ako i práca projektantov a technikov, ktorí ich podľa technických výkresov zobrazujú a zhotovujú,
je dnes bez znalosti zobrazovacích metód nepredstaviteľná. Nové metódy konštruovania s podporou počítačov ešte zvýšili nároky kladené na priestorovú predstavivosť
a schopnosť rekonštrukcie trojrozmerného objektu modelovaného a zobrazovaného v niektorej zo zobrazovacích metód na obrazovke počítača či na kresliacom zariadení.