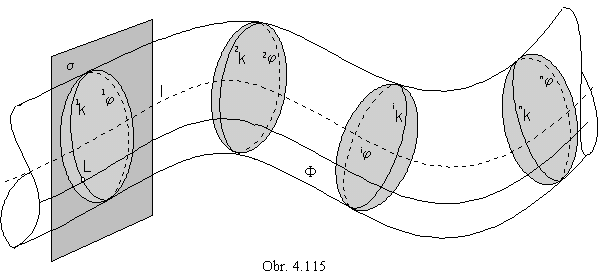
OBALOVÉ PLOCHY

Obalové plochy

Obálka sústavy plôch S = { ⁱφ }sa nazýva obalová plocha Φ, ak má nasledujúce vlastnosti:

a) obálka Φ a každá plocha ⁱφ zo sústavy sa dotýkajú v čiare - charakteristike ⁱk,

b) v každom bode obálky Φ existuje spoločná dotyková rovina a normála plochy Φ a jednej plochy ⁱφ zo sústavy,

c) neexistuje plocha, ktorá by bola súčasne časťou Φ a niektorej plochy ⁱφ zo sústavy.

Sústavu plôch S = { ⁱφ } získame z riadiacej plochy φ, ktorú podrobíme triede geometrických transformácií (obr. 4.115).

Obalová plocha je obálka obrazov riadiacej plochy φ v danej triede geometrických transformácií.

Syntetická reprezentácia: ( φ, T(w) )

Analytické reprezentácie:

riadiaci útvar - p(u, v) = (x(u, v), y(u, v), z(u, v), 1), (u, v) ∈ < 0, 1 >²

generujúci princíp - trieda geometrických transformácií T(w), w ∈ < 0, 1 >

modelovaný útvar - s(u, v, w) = p(u, v).T(w), ( u, v, w) ∈ < 0, 1 >³

Vektorová funkcia troch premenných s(u, v, w) reprezentuje trojparametrický útvar priestoru - masív,
obálka obsahuje body hranice masívu, spĺňajúce nižšie uvedenú podmienku (I).

Charakteristiku k, dotykovú čiaru plochy φ a obálky Φ,
nájdeme pomocou spoločnej dotykovej roviny τ
v ľubovoľnom bode L obálky.
Rovina τ je určená dotyčnicami so smerovými vektormi p_u, p_v,
ktoré sú vektormi dotyčníc parametrických čiar plochy φ.

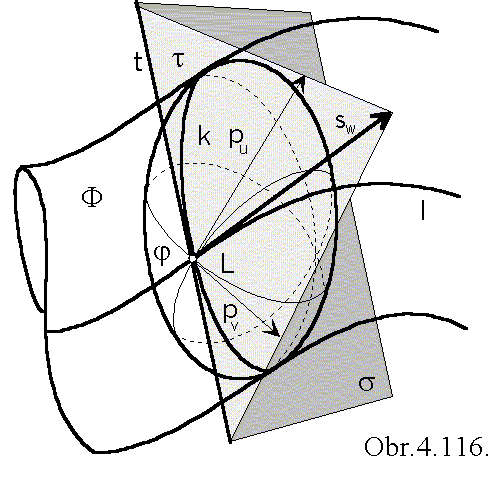
Dotyčnica čiary l, ktorá je na obálke dráhou pohybu bodu L,
leží tiež v dotykovej rovine τ,
jej smerový vektor s_w je komplanárny s vektormi p_u, p_v.
Zmiešaný súčin týchto troch vektorov dotyčníc
parametrických čiar masívu je nulový.

[p_u p_v, s_w] = 0 ....................... (I)

Charakteristika je čiara, obsahujúca všetky tie body plochy φ, v ktorých je splnená uvedená podmienka (I).
V prípade jednoduchých riadiacich plôch je to rez riadiacej plochy φ rovinou σ,
prechádzajúcou daným bodom L kolmo na vektor dotyčnice s_w dráhy pohybu.
Priesečnica rovín σ a τ je dotyčnica charakteristiky v bode L (obr. 4. 116).
Obalovú plochu možno vytvoriť aj z charakteristiky,
ak ju podrobíme takej istej triede transformácií ako pôvodnú riadiacu plochu φ.
Obalová plocha je jednoznačne určená charakteristikou k ( riadiacou plochou j) a triedou geometrických transformácií.

(φ, T(w) ⇔ (k, T(w))

Podľa typu generujúceho princípu delíme obalové plochy na:

homotetické (obr. 4.117), skrutkové(obr. 4.118), rotačné (obr. 4.119), translačné (obr. 4.120).

Riadiacou plochou je najčastejšie rozvinuteľná priamková plocha (napr. časť roviny) alebo rotačná plocha (napr. guľová plocha na obr. 4.117 až 4.120).

Obr. 4.117 Obr.4.118

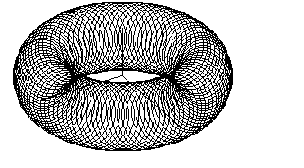
Obr. 4.119 Obr. 4.120

1. Obalové translačné plochy

Plochu φ podrobíme triede posunutí určenej vektorom a = (k, l, m, 0).

Na obr. 4.121 je priemet obálky sústavy rotačných kužeľových plôch v Mongeovej projekcii
a priemet obálky sústavy rotačných valcových plôch v kolmej axonometrii,
pričom trieda translácií je určená vektorom a.

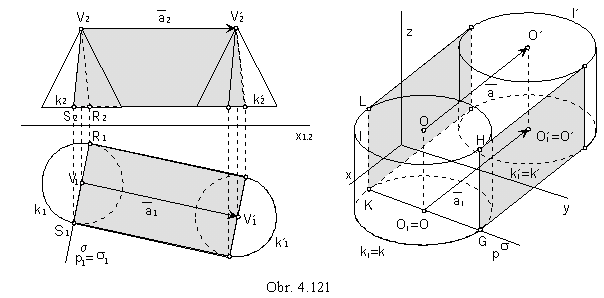
Charakteristika je lomená čiara SVR na kužeľovej ploche, dvojica úsečiek KL // GH na valcovej ploche,
ktoré sú rezmi riadiacich plôch rovinou s kolmou na smer a.

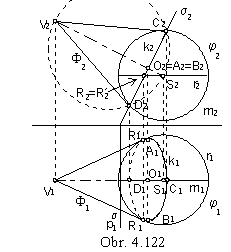
2. Obalové homotetické plochy

Plochu φ podrobíme triede rovnoľahlostí so stredom v bode V a koeficientom h = 1.
Charakteristika k je rezová čiara riadiacej plochy φ rovinou σ kolmou na priamku, ktorá je dráhou pohybu plochy φ.
Ak je riadiacou plochou guľová plocha,
charakteristika je dotyková čiara (kružnica) riadiacej guľovej plochy φ
a obalovej plochy Φ - rotačnej kužeľovej plochy.

Nech S je stred riadiacej guľovej plochy φ s daným polomerom (obr. 4.122).
Obrysové tvoriace priamky obálky Φ v náryse
sú dotyčnice nárysu hlavného meridiánu m₂ v bodoch C₂, D₂ prechádzajúce bodom V₂.
Nárysom charakteristiky k je úsečka C₂D₂
kolmá na nárys priamky SV (os obálky Φ).
Stred charakteristiky k leží na osi obálky.
Pôdorysom charakteristiky je elipsa (stred O₁, vedľajšie vrcholy C₁, D₁),
ktorej hlavná os (rovnobežná s p^σ) obsahuje hlavné vrcholy A₁, B₁
vo vzdialenosti polomeru a kružnice k od stredu O, a = |C₂O₂| = |O₂D₂|.
Viditeľnosť pôdorysu určíme pomocou dotykových bodov R a R´ obrysových tvoriacich čiar pôdorysu
(spoločné body čiar r a k v náryse).

3. Obalové rotačné plochy

Plochu φ podrobíme otáčaniu okolo osi o.
Vektor dotyčnice dráhy pohybu je kolmý na os otáčania
(kružnice ako dráhy pohybu ležia v rovinách kolmých na os).
Rovina σ charakteristiky k prechádza osou otáčania o
kolmo na vektor dotyčnice.

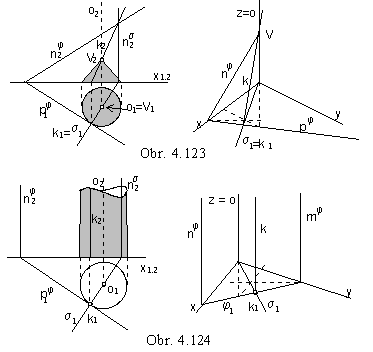
Otáčaním roviny φ obalíme rotačnú kužeľovú plochu K (obr. 4.123),
príp. valcovú plochu V (obr. 4.124).
Charakteristika k je priesečnica roviny φ
s rovinou σ, prechádzajúcou osou otáčania kolmo na rovinu φ.
Priesečník charakteristiky s osou otáčania je vrchol obalovej plochy
(vlastný bod pre K a nevlastný pre V).

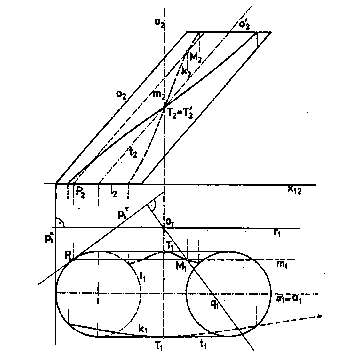
Nech je riadiacim útvarom obalovej rotačnej plochy šikmá kružnicová valcová plocha V s osou o´ rovnobežnou s nárysňou (obr. 4.125).
Na každej riadiacej priamke m plochy V nájdeme bod M charakteristiky k.
Priamku m nahradíme dotykovou rovinou τ plochy V v tejto priamke a nájdeme charakteristiku q roviny τ,
ktorú podrobíme otáčaniu okolo osi o (podľa obr. 4.123).
Tvoriaca priamka m pretína charakteristiku q dotykovej roviny t
v bode M hľadanej charakteristiky valcovej plochy V,
ktorou je Nikomedova konchoida s asymptotou v priamke o´.
Začiatočné a koncové body oblúkov charakteristiky k
na kružniciach l a l´ valcovej plochy nájdeme v rovinách,
ktoré prechádzajú osou triedy otáčaní o a stredmi kružníc l, l´.
Body T a T´, v ktorých sa mení viditeľnosť pôdorysu charakteristiky,
ležia na obrysových tvoriacich priamkach,
ktorých priemety sú totožné s priemetmi dotykových rovín (sú kolmé na pôdorysňu).

Obr. 4.125

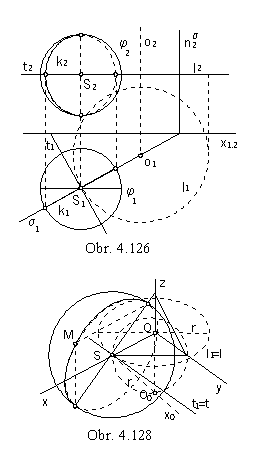
Na obr. 4.126 je zobrazená guľová plocha ako riadiaca plocha rotačnej obalovej plochy.
Rovina σ, kolmá na dotyčnicu t kružnice l (dráha pohybu) v bode S (stred guľovej plochy),
prechádza stredom guľovej plochy a osou otáčania a reže guľovú plochu v kružnici k, ktorá je charakteristikou.

Obr. 4.127

Ak je riadiacou plochou obalovej rotačnej plochy rotačná plocha φ s osou o´,
nájdeme body charakteristiky na rovnobežkovej kružnici k (stred O ∈ o´) plochy φ.
V čiare k sa plochy φ dotýka vpísaná guľová plocha G so stredom S na osi o´ (obr. 4.127).
Charakteristika guľovej plochy G (pri tom istom rotačnom pohybe okolo osi o) je kružnica h
ležiaca v rovine σ, ktorá prechádza stredom S a osou o.
Priesečníky M, M´ kružníc k a h sú body charakteristiky l.
Nie je potrebné nájsť nárys kružnice h, ktorá sa v pôdoryse zobrazuje ako úsečka.
Na obr. 4.127 je zobrazený hlavný meridián m vytvorenej obalovej rotačnej plochy.

V ortogonálnej axonometrii je zobrazená riadiaca guľová plocha φ so stredom S na súradnicovej osi x (obr. 4.128).
Trieda otáčaní je daná osou o v súradnicovej osi z.
Otočením pôdorysne do axonometrickej priemetne zistíme polomer kružnice l (dráha pohybu stredu S), r = |SO| = |SO₀|.
Axonometrický priemet kružnice l je elipsa.
(Hlavná os je priamka kolmá na os z, veľkosť hlavnej polosi sa rovná polomeru r kružnice l.
Z bodu S určíme rozdielovou konštrukciou dĺžku vedľajšej polosi premietnutej do axonometrického priemetu osi z).
Rovina σ prechádzajúca osou o kolmo na dotyčnicu t kružnice l v bode S (t // y) je nárysňa.
Rez plochy φ nárysňou je hlavná kružnica k - charakteristika.
Jej axonometrický priemet je elipsa s hlavnou osou v strane axonometrického trojuholníka a hlavnou polosou rovnou polomeru r.
Bod M elipsy nájdeme na rovnobežkách s priemetmi súradnicových osí x a z.
Rozdielovou konštrukciou určíme veľkosť vedľajšej polosi.
Výsledná obalová plocha je anuloid, kružnica k je meridián anuloidu.

4. Obalové skrutkové plochy

Plochu φ podrobíme skrutkovému pohybu určenému osou, orientáciou a redukovanou výškou závitu z₀.
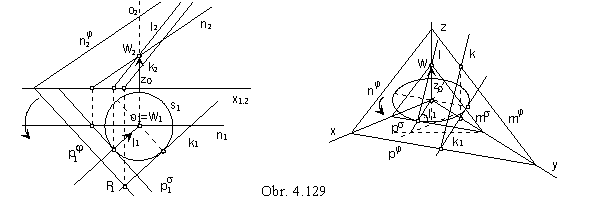
Na obr. 4.129 je riadiacou plochou rovina φ, rôznobežná s osou skrutkového pohybu o kolmou na pôdorysňu.
Charakteristika k je priamka obalovej skrutkovej plochy, ktorá je plochou dotyčníc skrutkovice vratu s.
Rovina φ je oskulačnou rovinou skrutkovice vratu s,
hľadaná charakteristika k je jej dotyčnicou ležiacou v rovine φ.
Kužeľová plocha dotyčníc K skrutkovice vratu (vrchol W ∈ o, | Wπ | = z₀)
obsahuje priamku l rovnobežnú s charakteristikou k,
v priamke l sa plochy K dotýka rovina σ rovnobežná s oskulačnou rovinou φ skrutkovice vratu s
(s určíme hlavnou priamkou n a nájdeme jej stopy).

Skrutkovým pohybom guľovej plochy vznikne sústava plôch S, ktorých obálkou je Archimedova serpentína (obr. 4.110).

Stred guľovej plochy sa pohybuje po skrutkovici s,
ktorej kužeľová plocha dotyčníc K má vrchol W ∈ o a jej riadiaca kružnica h leží v rovine π^S,
prechádzajúcej bodom S rovnobežne s pôdorysňou (obr. 4.130).
Dotyčnicu t skrutkovice s (dráha pohybu bodu S) nájdeme pomocou tvoriacej priamky l

K.
Stredom S prechádza rovina σ kolmá na priamku t,
ktorá reže riadiacu guľovú plochu v hlavnej kružnici - charakteristike k.
Rovinu σ určíme hlavnými priamkami kolmými na priamku t, σ = pn .
Priesečníky priamok p a n s guľovou plochou sú body
A, B ∈ p (premietnuté do hlavných vrcholov priemetu k v pôdoryse),
A´, B´ ∈ n (v priemete hlavné vrcholy nárysu k).
Rozdielovou konštrukciou určíme veľkosti vedľajších polosí
priemetov charakteristiky k.

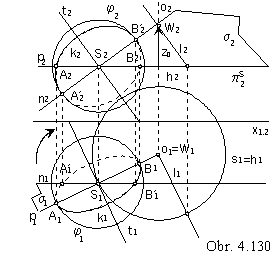
Hlavný meridiánový rez Archimedovej serpentíny je na obr. 4.131.
Rezová krivka m = μ ∩ Φ je obálkou kružníc, ktoré sú rezmi guľových plôch sústavy S rovinou μ.
Nájdeme ich ako vyskrutkované kružnice, ktoré sú rezmi riadiacej guľovej plochy φ meridiánovými rovinami,
do roviny hlavného meridiánu μ.
Stačí určiť stredy L*, H* kružníc l*, h* ako vyskrutkované polohy stredov L, H do roviny μ.
Ak pre uhly ω a ω´ otočenia platí

ω^S - ω´ = ω - ω^S

potom pre odpovedajúce posunutia z^L a z^H v danom skrutkovom pohybe s výškou závitu zv platí:

z^S - z^H = z^L - z^S

Body L* a H* (a kružnice l* a h*) sú súmerne združené podľa osi rezovej čiary
prechádzajúcej bodom S* (vyskrutkovaný stred guľovej plochy) kolmo na os skrutkového pohybu o.

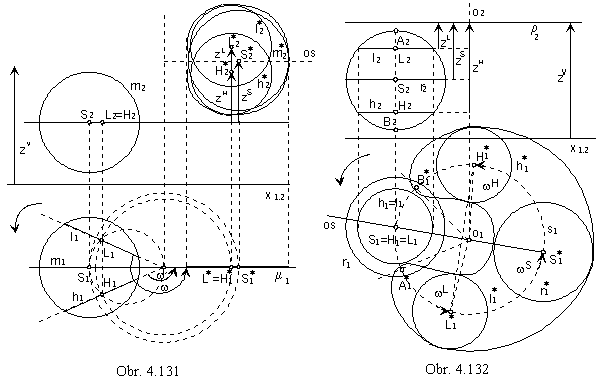
Normálový rez Archimedovej serpentíny (kolmou rovinou ρ na os o skrutkového pohybu)
nájdeme obdobne ako meridiánový rez (obr.4. 132).
Rezy riadiacej guľovej plochy normálovými rovinami skrutkujeme do roviny ρ.
Všetky stredy rezových kružníc sa pohybujú po skrutkoviciach zobrazených do jednej kružnice v pôdorysni.
Ak pre posunutia z^L a z^H bodov L, H platí

z^H - z^S = z^S - z^L

pre odpovedajúce uhly otočenia platí

ω^S - ω^L = ω^H - ω^S

Body L* a H* a kružnice l* a h* sú súmerne podľa osi rezovej čiary (obálky všetkých vyskrutkovaných kružníc)
prechádzajúcej bodom S* kolmo na os skrutkového pohybu.
Uhly otočenia a im odpovedajúce dĺžky posunutí v danom skrutkovom pohybe určíme pomocou Archimedovej špirály.

Pri konštrukcii charakteristiky obalovej plochy,
ktorá vznikne skrutkovým pohybom priamkovej (rotačnej) plochy,
nahradíme tvoriacu priamku (rovnobežkovú kružnicu) riadiacej plochy
dotykovou rovinou plochy v tejto priamke (vpísanou guľovou plochou dotýkajúcou sa plochy v tejto kružnici).
Dotykovú rovinu (guľovú plochu) podrobíme skrutkovému pohybu a nájdeme jej charakteristiku.
Spoločné body zvolenej tvoriacej priamky (rovnobežkovej kružnice) a tejto charakteristiky
sú bodmi hľadanej charakteristiky obalovej skrutkovej plochy.
Na obr. 4. 133 je takto zostrojená charakteristika obalovej skrutkovej plochy,
ktorej riadiacou plochou je: a) valcová plocha, b)všeobecná rotačná plocha.

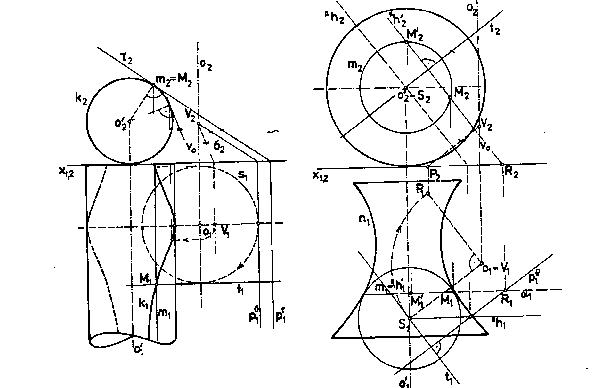
Obr. 4.133