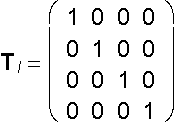
Euclidean transformations

Euclidean - metric transformations preserve invariant size of the figure, they change only the figure position in the space.
Relation between coordinates of the original and its image in the given transformation is expressed by equations of the transformation.
Matrix of a linear transformation is the matrix of this system of linear equations:

(x, y, z, 1) ® (x´, y´, z´, 1)

x´ = f(x, y, z),

y´ = g(x, y, z),

z´ = h(x, y, z)

A´ = A .T


Identity


   x´ = x

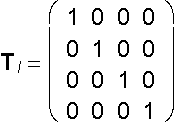
   y´ = y

   z´ = z


  A´ = A .TI




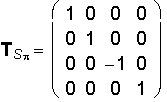
Symmetry with respect to the coordinate plane p = xy


x´ = x

y´ = y

z´ = -z


  A´ = A .TSp




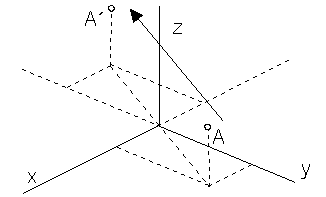
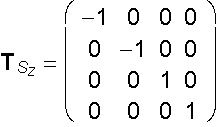
Symmetry with respect to the coordinate axis z


x´ = - x

y ´ = - y

z´ = z


  A´ = A .TSz

Symmetry with respect to the origin O


x´ = - x

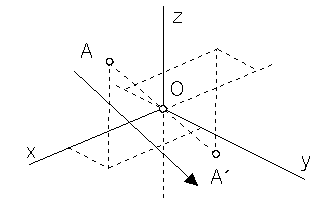
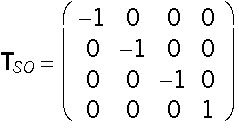
y ´ = - y

z´ = -z

A´ = A .TSO




Revolution about the coordinate axis z by angle j


x´= x cosj - y sinj

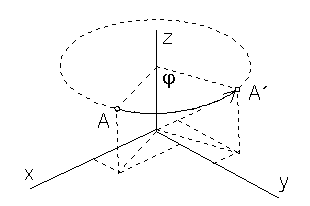
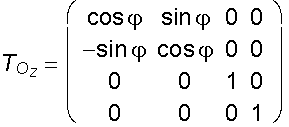
y ´= x sinj + y cosj

z´= z

A´= A .TOz




Translation by vector (m, n, p, 0)


x ´= x + m

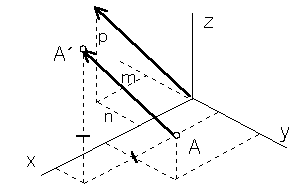
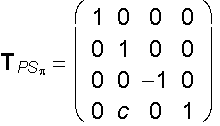
y ´= y + n

z´= z + p

A´= A .TP


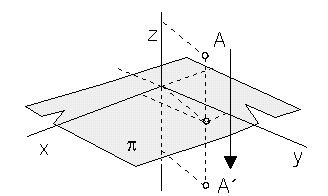
Symmetry with respect to the coordinate plane p
translated by vector (0, c, 0, 0)


x ´= x

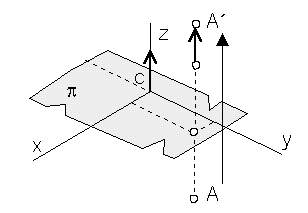
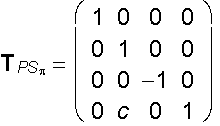
y ´= y

z´= -z + c

A´= A . TPSp


Symmetry with respect to the coordinate axis z translated by vector (c,0,0,0)


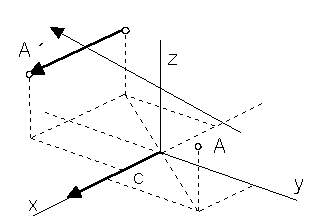
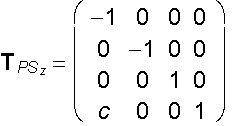
x´= - x + c

y´ = - y

z´ = z

A´ = A . TPSz


Symmetry with respect to the coordinate plane m
revolved about the coordinate axis x


x´ = - x

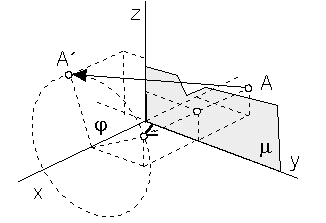
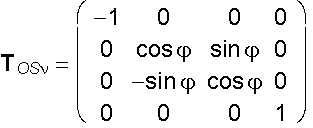
y´ = y cosj - z sinj

z´ = y sinj + z cosj

A´ = A . TOSn


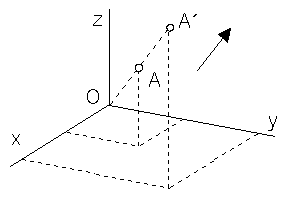
Helical movement about the coordinate axis z with the translation vector (0,0,v,0) related to the revolution angle j


x ´ = x cosj - y sinj

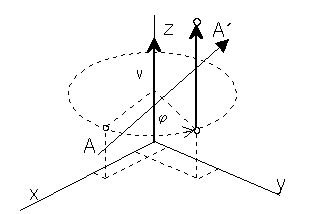
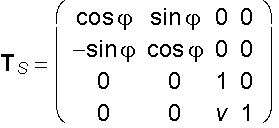
y ´ = x sinj + y cosj

z´ = z +v

A´ = A . TS

Determinant of the matrix TM of any metric transformation has the value ±1, it is valid |TM|2 = 1.

 

Affine transformations of the space

Affine transformations do not preserve invariant the size of line segments and angles.
Special subset of affine transformations form similarities, preserving invariant the size of angles.
Any Euclidean transformation is an affine transformation (similarity) in .

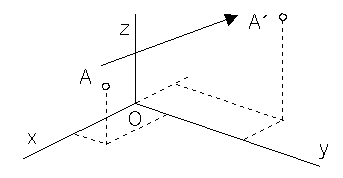
Scaling to the centre O
with the nonzero coefficient s (scale on all coordinate axes)


x´ = sx       x´ = x

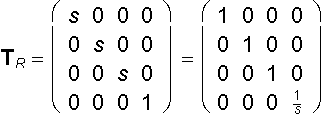
y´ = sy      y´ = y

z´ = sz      z´ = z

h = 1      h ´=

A´ = A . TR = (sx, sy, sz, 1) = s(x, y, z, )

Composition of scalings on coordinate axes x, y and z with centres in the origin
and nonzero scale coefficients a, e, i (on coordinate axes respectively)
is an affine transformation, which is not a similarity any more.

Scaling on coordinate axes x, y and z
with scale coefficients a, e, i respectively


x´ = ax

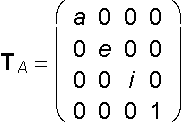
y´ = ey

z´ = iz

h = 1

A´ = A . TR = (ax, ey, iz, 1)



General affine transformation

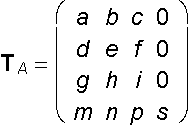| TA| 0, is matrix of the system of equations


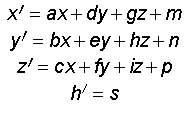
A = (x, y, z, 1) ®

Coefficients a to i, m, n, p, s 0 have clear geometric interpretation:

a, e, i - nonzero scales on coordinate axes x, y, z

s - coefficient of scaling to the origin

m, n, p - coordinates of the translation vector

b, c, f, d, g, h - coefficients of the general affine transformation.


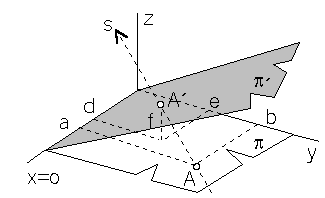
Axial affinity between planes
p = xy and p´ = xA´ with the axis in the coordinate axis x
and a pir of corresponding points A(a, b, 0, 1) ® A'(d, e, f, 1), b ¹ 0, f ¹ 0,
in the direction of affinity determined by the line s = AA'
with the direction vector s = (d - a, e - b, f, 0)


x´ = bx + (d - a)y

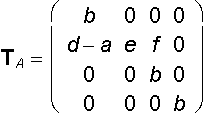
y ´ = ey

z´ = fy + bz

h´ = b

A´ = A . TA = (bd, be, bf, b) = b(d, e, f, 1)

 

 

Projective transformations of the space

Projective transformation of the extended Euclidean space E3 is any linear geometric transformation of the space called collineation.
In addition to incidence, collinear transformations preserve invariant ration of four points on a line.
All Euclidean and affine transformations are collineations with special properties and invariant elements.

General projective transformation

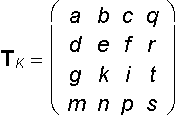s 0, |TK | 0, matrix of the system of equations

h

 

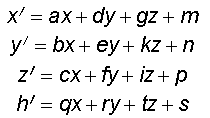
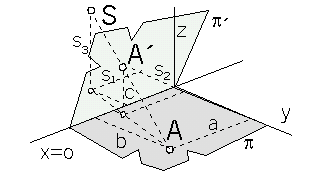
Central collineation between planes
p = xy and p´ = xA´
with the axis in the coordinate axis x,
centre in the point S = (s1, s2, s3, 1),
and a pair of corresponding points

A = (a, b, 0, 1) ® A´ = (x´, y´, c, 1), s3 0, b 0, c s3


(x, y, z, 1) ® (x´, y´, z´, h´)

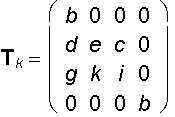
x´ = bx + dy + gz

y´ = ey + kz

z´ = cy + iz

h´ = hb

A´ = A .TK = (ab2 + bd, be, bc, b) = b(ab + d, e, c, 1)

d = , e = b - 1 + , g , k , i = b - .