Degree of the intersection curve of these two surfaces is n.m.
If there exists common plane of symmetry s of surfaces F and Y,
intersection curve is projected perpendicularly to the plane s (or to planes parallel to s)
to the curve of the degree
Intersection of Surfaces
Set of all points located on two different surfaces F and Y is the intersection of given surfaces.
Intersection can be:
an empty set FÇY={ }
surfaces have no common points
a finite set of points FÇY={R, S, T, ...}
surfaces have common isolated points and tangent planes in them
an infinite set of points FÇY=c
surfaces have common intersection curve, or more curves.
Let the degree of the surface F be n and the degree of the surface Y be m.
Degree of the intersection curve of these two surfaces is n.m.
If there exists common plane of symmetry s of surfaces F and Y,
intersection curve is projected perpendicularly to the plane s (or to planes parallel to s)
to the curve of the degree
![]() .
.
Construction of the Intersection
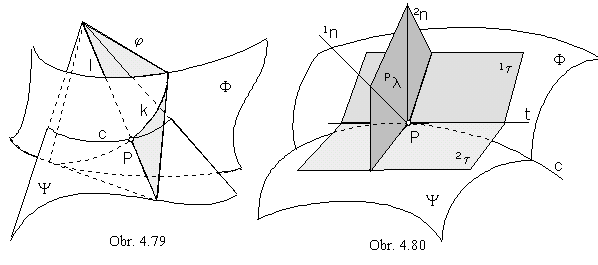
Arbitrary point P on the intersection curve c is the point located on both surfaces F and Y,
it is therefore located on some curve k on the surface F and on some curve l on the surface Y, while k Ç l = P (Fig. 4. 79).
Curves k, l are located on one surface j, which intersects surface F in the curve k and surface Y in the curve l.
In the construction of points on the intersection curve of surfaces F and Y we choose the system of auxhiliary surfaces, for which the following is valid:
![]()
![]()
![]()
Common points of curves ik and il (if they exist) are points on the intersection curve c.
Auxhiliary surfaces ij from the system are usually aptly chosen planes or spheres,
with regard to the intersecting surfaces F and Y,
in order to receive points on the intersection in the most precise and easy way.
Tangent line t in the point P on the intersection curve c
is located in the tangent planes 1t and 2t to surfaces F and Y in the point P
(it is curve located on both surfaces and passing through the point P),
it is the intersection line 1t Ç 2t = t (Fig. 4. 80).
Tangent line t
![]() 1t is located in the plane perpendicular to the normal 1n to the surface F in the point P,
1t is located in the plane perpendicular to the normal 1n to the surface F in the point P,
it is perpendicular to this line and also to the line 2n, normal to the surface Y in the point P,
![]() , because t
, because t
![]() 2t.
2t.
Line t is perpendicular to the plane Pl=1n2n, normal plane to the intersection curve c in the point P.
Calculation of coordinates of the intersection curve pooint
Analytic representation of the surface F is the point function
1p(u, v)=(1x(u, v), 1y(u, v), 1z(u, v), 1), (u, v)Î<0,1>2
and of the surface Y the point function
2p(s, t)=(2x(s, t), 2y(s, t), 2z(s, t), 1), (s, t)Î<0,1>2
If P is the point located on the intersection curve,
then there exist pairs of curvilinear coordinates (u0, v0) and (s0, t0 ) from the interval <0,1>2 such, that
P=1p(u0, v0)=(1x(u0, v0),1y(u0, v0),1z(u0, v0),1) = 2p(s0, t0)=(2x(s0, t0),2y(s0, t0),2z(s0, t0), 1) .
For arbitrary u0Î<0,1> we find numbers s0, t0, v0 Î<0,1>
as solutions of the system of three equations with three unknown.
1x(u0, v) - 2x(s, t)=0
1y(u0, v) - 2y(s, t)=0
1z(u0, v) - 2z(s, t)=0
System can be solved analytically, or by some from iteration methods of numerical analysis.
If there exist more solutions of the system, more points on the intersection curve are obtained
1P( u0, 1v0) = 1P( 1s0, 1t0), 2P( u0, 2v0) = 2P( 2s0, 2t0), ...
Found points are intersections of the v-parametric curve on the surface F (for u=u0) with the surface Y.
Intersections of surfaces of revolution
With respect to the superposition of the axes 1o, 2o of intersecting surfaces of revolution 1F, 2F
the suitable system of auxhiliary surfaces can be:
1. system of planes perpendicular to both axes 1o // 2o
2. system of concentric spheres with the common centre in the point S=1o Ç 2o
3. system of spheres with centres on one of the skew axes 1o / 2o
1. Intersections of surfaces of revolution with parallel axes
If the axes of surfaces coincide, intersection (if it exists) is the set of common parallel circles (Fig. 4. 88).
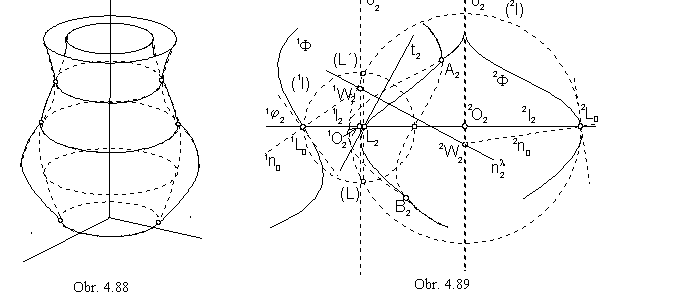
In the Fig. 4. 89 there is illustrated the front view of the intersection of surfaces of revolution with parallel axes located in the frontal image plane.
Outlines of surfaces are located in the frontal image plane and they have common points A, B of the intersection k.
Plane 1j from the system of planes perpendicular to both axes (according to 1.), and therefore to the frontal image plane, intersects both surfaces in parallel circles 1l, 2l projected to line segments. Common points of these circles are points of intersection curve
1lÇ 2l={L,L´}, L,L´Îk
Intersection curve k is symmetric with respect to the frontal image plane (similarly as both surfaces),
points L and L´ are projected to the frontal image plane to one point. Points can be found
by lowering the plane 1j to the frontal image plane about its intersection line with the frontal image plane, line 1O 2O.
Points 1O, 2O are centres of circles 1l, 2l located on axes 1o, 2o.
Tangent line to the intersection curve in the point L can be determined as the line perpndicular to the normal plane l
defined by normals 1n, 2n to the surfaces 1F, 2F in the point L.
Traces of normals 1W, 2W are located on axes and they can be determined by normals to the surfaces in the points
1L0, 2L0, which are revolved positions of the points 1L, 2L to the image plane on parallel circles 1l, 2l.
In the start and end point of the intersection curve view the tangent line can be determined without revolving them
to the image plane, points are located directly in the image plane.
2. Intersections of surfaces of revolution with intersecting axes
Intersection point S of axes of two surfaces of revolution is the centre of the spheres in the system (according to 2.).
Any of the spheres intersects both surfaces in parallel circles.
Common points of these parallel circles are points on the intersection curve.
 In the Fig. 4. 90 there is the front view of the intersection
In the Fig. 4. 90 there is the front view of the intersection
of surfaces 1F, 2F with intersecting axes 1oÇ2o=S
located in the frontal image plane
(denotations of views by indeces are excluded in the figure).
One of the spheres G shares with intersecting surfaces
common circles 1l, 1l´, 2l, 2l´ ,
projected in front views as line segments.
Their common points K, L, M are located on the intersection
2lÇ1l´=K 2l´Ç1l´=L 1lÇ2l=M
Other points on the intersection can be found as the intersection points of outlines, they are both located in the image plane.
Tangent line t in the point M can be determined by the same construction as in the case of surfaces with parallel axes.
Intersections of quadratic surfaces of revolution
If there exists a common plane of symmetry of two quadratic surfaces of revolution 1F, 2F with axes 1o, 2o
(1o // 2o, or 1o Ç 2o = S),
then their intersection curve is projected orthogonaly to this plane (and to all parallel planes)
as a conic section or a part of it.
If the axes are intersecting lines, the view is a segment of a central conic section,
in the case of parallel axes the view is a segment of a parabola
with the axis perpendicular to views of both axes of surfaces of revolution.
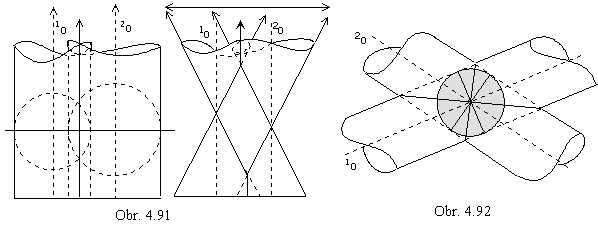
An exception is the intersection of two cylindrical surfaces of revolution,
or two conical surfaces of revolution with equal angles that surface lines form to the surfaces axes,
when the intersection is projected to one real line,
or to the pair of halflines and one ideal line (Fig. 4. 91).
Intersection is a pair of common parallel lines on cylindrical surfaces,
or common hyperbolas on conical surfaces (one branch from each hyperbola) and common ideal parallel circle.
Intersection of two cylindrical surfaces of revolution with parallel axes split to two ellipses if there exists a sphere inscribed into both surfaces, with the centre in the intersection point of surface axes (surfaces have the same radii).
View of the intersection curve in the common plane of symmetry is in the pair of line segments (Fig. 4. 92).
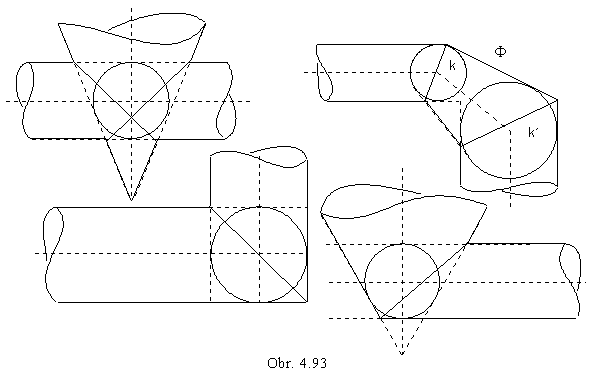
The special split intersection of two cylindrical, or conical surfaces of revolution is applied in the practise in the pipe-line technics, some illustrations of the adjoinings of cylindrical and conical pipe lines are given in the Fig. 4. 93.
Centre of the inscribed sphere is in the intersection point of axes of intersecting quadratic surfaces of revolution.
Surface F is developable transition surface determined by circles k and k´.
In the Fig 4. 94, the front view of the intersection of cylindrical - V and conical - K surfaces of revolution is constructed
by the method of the system of spheres with centres in the intersection point of both surface axes.
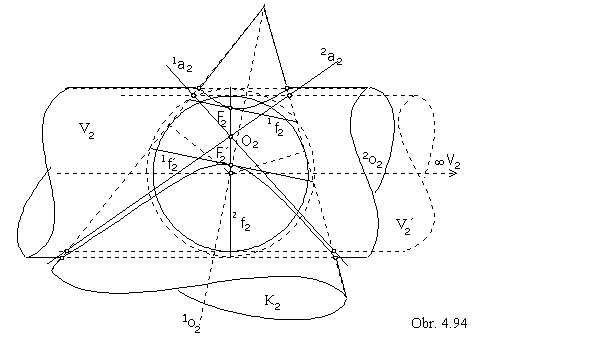
On the sphere tangent to the surface V in one parallel circle 2f, and intersecting the surface K in two parallel circles 1f and 1f´, points F and F´ of intersection in the extremal distances from the image plane are located.
Tangent lines to the intersection curve in these points are projected to lines coinciding with line segments,
which are views of parallel circles 1f and 1f´.
View of the intersection is a part of hyperbola, boundary points of hyperbolic segments are in the intersection points of outlines of both surfaces.
Line segment FF´ is one diameter of hyperbola, centre is located in its centre O.
Asymptotes 1a, 2a can be found from the intersection of the surface K with the surface V´,
sharing the common ideal vertex
![]() V with the surface V (surfaces V and V´ have parallel generating lines).
V with the surface V (surfaces V and V´ have parallel generating lines).
Both surfaces are subscribed to one sphere, their intersection split to two conic sections.
Diagonals of the fourgone with vertices in the intersection points of outlines of surfaces V´ and K are asymptotes of the hyperbola - view of the intersection curve of quadratic surfaces.
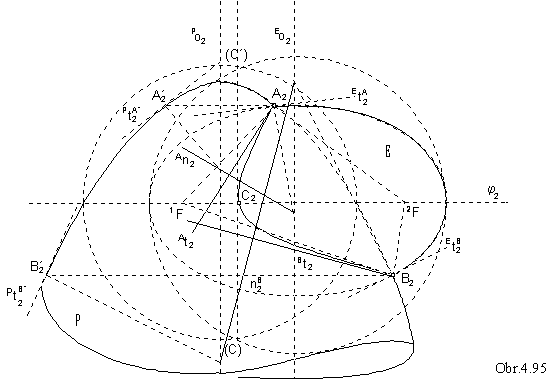
Intersection of the paraboloid of revolution and the ellipsoid of revolution with parallel axes is in the Fig. 4. 95.
System of planes perpendicular to both axes intersects both surfaces in parallel circles, their common points are points on the intersection curve. Its view - parabolic segment - has boundary points A, B in the intersection points of ourlines.
Tangent lines in these points can be constructed by means of normal planes in the same way, as in the Fig. 4.89.
Tangent line in the highes point C on the intersection curve with respect to the frontal image plane is projected to the line in the view of the equator circle r on ellipsoid, CÎ r.
3. Intersections of surfaces of revolution with skew axes
Method of construction of the intersection curve depends on the type of intersecting surfaces.
System of auxhiliary spheres can be chosen in such way, that the
intersection curves of spheres and both given surfaces are elementary curves (lines, or circles).
In very complicated problems we choose planes perpendicular to axis of one surface,
then the intersection curves are parallel circles, while intersection curves with the other surface must be constructed.
Very popular surface in the technical practise - torus (anuloid) intersects quadratic surfaces of revolution
in the curve of degree 8, which often split to several parts.
These intersection can be esily constructed in the orthographic view to image plane perpendicular to the torus axis 1o,
while the axis of the quadratic surface 2o is located in the image plane, lines 1o, 2o are skew.
Outlines of surfaces are located in image plane and intersect in the intersection curve segment boundary points.
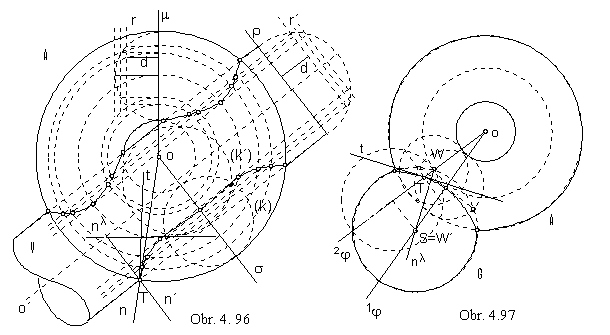
Intersection of torus and cylindrical surface of revolution, or of two toree can be constructed by means of the system of planes parallel to the image plane. Planes intersect cylindrical surface in pairs of lines, toree in parallel circles.
Views of these curves located in plane ij in the distance d from the image plane can be found
by lowering the meridian circles on the toree (intersection by plane m passing through the axis o)
and basic circle on the cylindrical surface (intersection by plane r perpendicular to the axis o´) Fig. 4. 96, 4. 98.
Intersection lines r and r´ of planes m and r with the plane ij have common points with seeked curves
on intersecting surfaces, which can be constructed from the lowered intersections.
Extremal points on intersection curves are located in the tangent plane ij to one from the intersecting surfaces.
Intersection in the Fig. 4. 96 is symmetric with respect to the plane s passing through the torus axis o
perpendicularly to the axis o´ of the cylindrical surface, and intersecting sufaces in circles k and k´.
Intersection of torus and sphere can be constructed by system of planes with a common line in the torus axis.
Any plane ij from the system intersects both surfaces in circles projected to line segments.
Their common points are found by lowering the plane ij to the image plane (Fig. 4. 97).
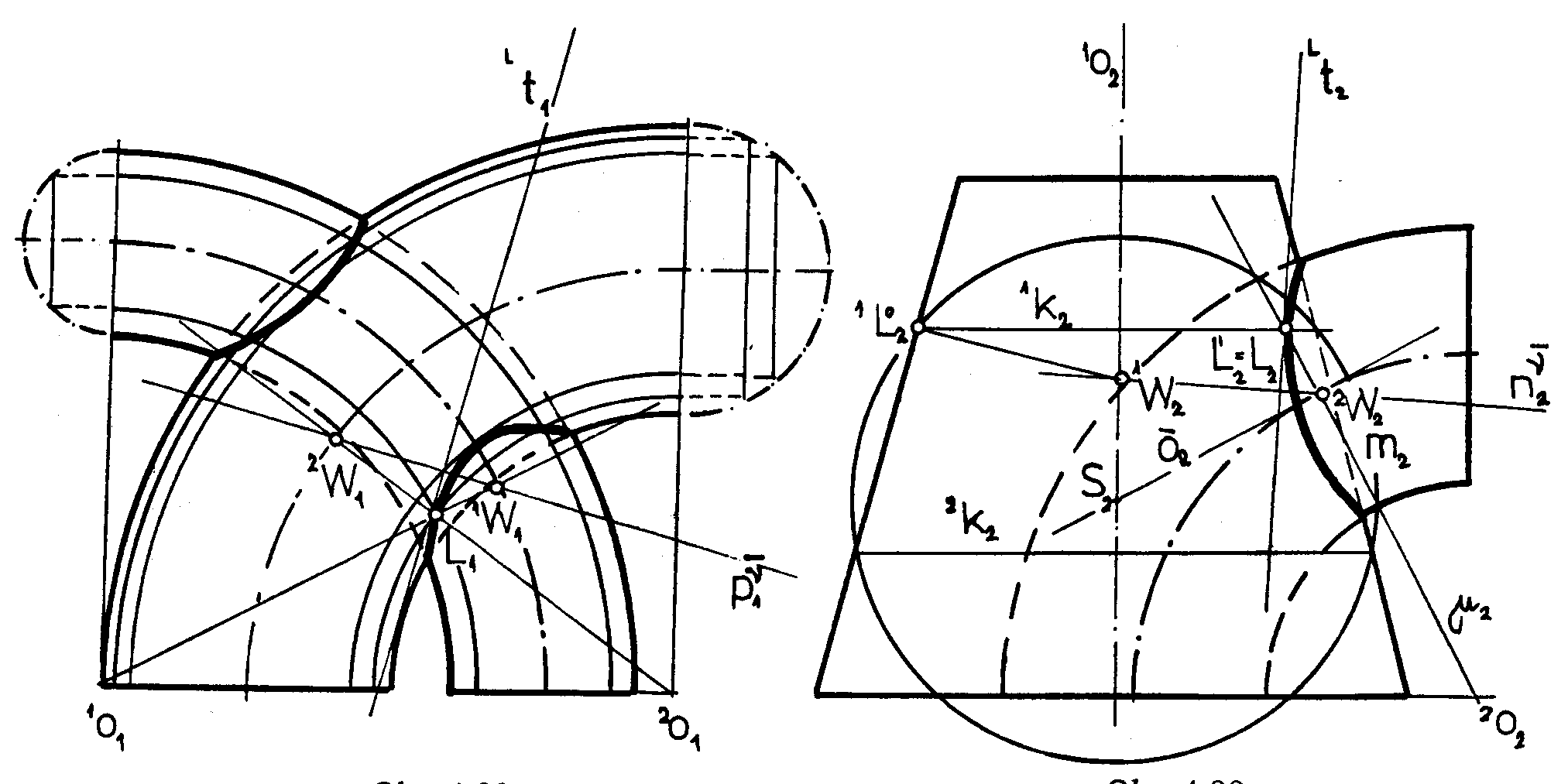
In the construction of the intersection of torus and conical surface of revolution, the system of spheres
with the centres on the axis of the conical surface is used (spheres intersect conical surface in circles).
Chooing a circle m on the torus (Fig. 4. 99), which is an intersection by the meridian plane m
projected to the image plane (passing through the axis 1o of the conical surface perpendicularly to the torus axis 2o)
as a line segment, the sphere from the system is determined.
Line passing through the circle m centre 2W ( on the axial torus circle) and perpendicular to the meridian plane m
intersects the axis 1o in the centre S of the sphere ( m is its planar ingersection by m ).
Sphere intersects conical surface in parallel circles 1k and 2k projected to line segments.
Common points of circles m, 1k and 2k are points on the intersection curve.
In all problems, the tangent line to the intersection curve in the point T can be constructed
as the line perpendicular to the normal plane l determined by normals to both surfaces in the given point.
All normals to sphere are passing through the sphere centre,
normals to conical and cylindrical surfaces of revolution are perpendicular to surface lines,
normals to torus in the points on one meridian circle are located in the meridian plane
and they have a common point in the centre of this circle on the axial torus circle.
Trace of the normal plane is determined by traces of normals.