Revolving an ellipse about its major axis 1o (minor axis 2o) an ellipsoid of revolution prolate (oblate) can be created (Fig. 4. 59).
QUADRATIC SURFACES of REVOLUTION
Quadratic surfaces (surfaces of degree 2) are all surfaces, which have at most two intrsection points with a line.
We can speak about two different types of quadratic surfaces, singular (cylindrical and conical) and regular (sphere, ellipsoid, paraboloid and hyperboloid).
Regular quadratic surfaces of revolution can be created by revolving the conic section about its axis.
1. Ellipsoid of revolution
Revolving an ellipse about its major axis 1o (minor axis 2o) an ellipsoid of revolution prolate (oblate) can be created (Fig. 4. 59).
 b, a
b, a
 0, b
0, b
 0
0
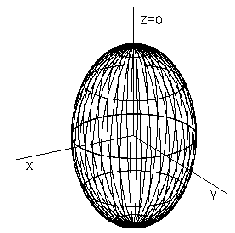
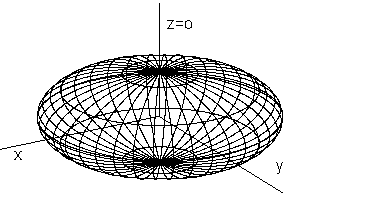
Fig. 4. 60 a Fig. 4. 60 b
Planar intersection of the ellipsoid of revolution can be in the form of:
a) a circle, if the intersection plane is perpendicular to the surface axis,
b) an ellipse in all other cases.
Planar intersection of the ellipsoid of revolution by the plane,
which is not perpendicular to the surface axis,
is the ellipse e (Fig. 4. 61).
Axis of the intersection ellipse ground view are mapped to
the principle and slope line of the first frame in the intersection plane.
Intersections of these lines with the ellipsoid are vertices of the intersection e ground view, pionts A, B, C, D.
Ground view of the intersetion is tangent to the outline of the ellipsoid in the ground plane,
which is the ground view of the equator circle,
in the points K, L, in which the equator intersects the intersection plane.
The intersection curve segment KL located over the equator of the ellipsoid of revolution is visible in the ground view.
Front view of the intersection is determined by
the related diameters located in the front views of the principle and slope line,
with the end points in the front views of the ground view vertices.
Axis and vertices of the intersection ellipse front view can be constructed by the Rytz method.
Front view of the intersection is tangent to the principle meridian m in its intersections with the intersection plane,
in the points M, N. Segment of the intersecion ellipse NM located in front of the principle meridian m is visible in the front view.
All eight defining points of the intersection ellipse can be found by
methods used in the construction of the planar intersection on the general surface of revolution,
or by means of the additional third orthographic view to the new image plane,
side plane perpendicular to the ground image plane and to the intersection plane,
in which the intersection ellipse appears as a line segment (Fig. 4. 62).


In the construction of the intersection points of a line and an ellipsoid of revolution, the second projecting plane l of the given line perpendicular to the frontal plane can be used.
The superposition of the line a and the ellipse,
which is the planar intersection of the surface by plane l,
determines the superposition of the line and the ellipsoid of revolution (Fig. 4. 63).
Visibility of the line with respect to the ellipsoid of revolution can be determined according to the visibility of the intersection ellipse. Visible part of the intersection ellipse is bounded by the points of intersection of this curve and the equator of the ellipsoid of revolution.
2. Paraboloid of revolution
Revolving a parabola about its axis a paraboloid of revolution can be created (Fig. 4. 64).
 0
0 Axonometric view of the paraboloid of revolution is in the Fig. 4. 65.
Planar intersection of the paraboloid of revolution can be in the form of:
a) a circle, if the intersection plane is perpendicular to the surface axis,
b) a parabola, if the intersection plane is parallel (coincidental) to the surface axis,
c) an ellipse in all other cases.
Theorem: Orthographic view of an ellipse located on the paraboloid of revolution
under the mapping to the plane perpendicular to the axis of the paraboloid is a circle.
Elliptic intersection of the paraboloid of revolution can be constructed
in the same way as the elliptic intersection of the ellipsoid of revolution,
while the ground view of the intersection ellipse is a circle (Fig. 4. 67).
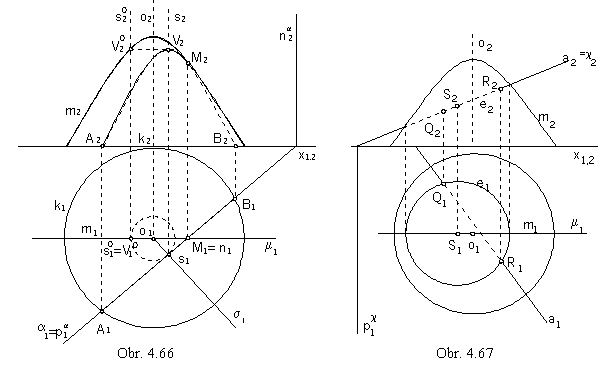
Planar intersection of the paraboloid of revolution patch by plane r parallel to the surface axis is in the Fig. 4. 66.
Plane r is perpendicular to the ground image plane p, ground view of the intersection parabolic segment is a line segment I1J1. End points are ground views of the intersection points of the parallel circle k on the paraboloid located in ground image plane with the intersection plane, it means, with the trace of then plane in the ground image plane.
Points I and J are end points of the intersection parabolic segment.
Tangent lines to the front view of the intersection in the front views of these points can be found by the properties of the parabola subtangent.
Axis of the intersection parabolic segment is the slope line 1s in the intersection plane (parallel to the surface axis),
intersection point of this line and surface is the vertex V of the intersection parabola.
Intersection plane r intersects the plane m of the paraboloid principle meridian
in the principle line of the second frame n, which has the intersection point M with the principle meridian.
This is the tangent point of the intersection curve front view with the surface outline in the frontal image plane.
In this point, the visibility of the front view changes,
the part of the intersection parabolic segment located in front of the principle meridian plane is visible.
Intersection points of the line and paraboloid of revolution
can be costructed in the same way,
as intersection points of the line and ellipsoid of revolution (Fig. 4. 67).
Frontal projecting plane of the line a intersects paraboloid of revolution in the ellipse e
appearing in the front view as the line segment and in the ground view as the circle.
Intersection points of the ellipse e and the line a
are common points Q, R of the line a and paraboloid of revolution.
3. Hyperboloid of revolution
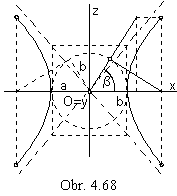
 0, are hyperbola semiaxes
0, are hyperbola semiaxes  0 are hyperbola semiaxes
0 are hyperbola semiaxes

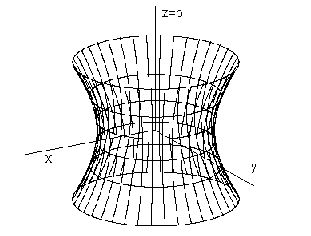
Fig. 4. 69
In the Fig. 4. 69 the axonometric views of one-sheet hyperboloid of revolution with axis in the coordinate axis z
and two-sheet hyperboloid of revolution with axis in the cooridnate axis x are illustrated.
Planar intersection of the hyperboloid of revolution can be in the form of:
a) a circle, if the intersection plane is perpendicular to the surface axis,
b) a conic section in other cases.
Intersection plane intersects hyperboloid of revolution H and its asympthotic conical surface AK in the conic section of the same type.
Let s be the vertex plane to the asympthotic conical surface AK parallel to the intersection plane r.
Intersection of the hyperboloid of revolution H by the plane r will be in the form of:
a) a hyperbola b) a parabola c) an ellipse, or a circle,
If the plane s intersects the asympthotic conical surface AK in:
a) a pair of lines b) one line c) one point, vertex of AK.
Elliptic intersection of the hyperboloid of revolution can be constructed in the same way as the elliptic intersection of the ellipsoid of revolution.
Vertex plane s intersects asympthotic conical surface AK in the vertex V.
Parabolic intersection of the hyperboloid of revolution can be constructed similarly
to the parabolic intersection of the paraboloid of revolution.
Vertex plane s is the tangent plane to the asympthotic conical surface AK in the common line,
which is parallel to the intersection parabola axis,
and which appears in the ground view as the axis of the intersection parabola ground view.
Intersection points of the slope line 1s in the intersection plane and the hypeboloid is the vertex of the intersection,
projected in the ground view to the vertex of the intersection parabola ground view.
It can be found in the same way as in the parabolic intersection of the paraboloid of revolution,
although the slope line 1s in the intersection plane is not parallel to the axis of the hyperboloid,
but intersects the axis in the point R, invariant in the revolution of the line 1s about the surface axis,
to the position parallel to the frontal plane.
The start point and the end point of the visualised parabolic intersection segment
are located on the trace of the intersection plane in the ground image plane and on the parallel circle,
in which the ground image plane intersects hyperboloid.
Only one from the pair of lines p, 1s (principle and slope line of the first frame in the intersection plane)
intersects hyperboloid of revolution in the major vertices A, B of the intersection hyperbola.
In the intersection of the hyperboloid of two sheets, it is always the slope line 1s,
in the intersection of the hyperboloid of one sheet it can also be the principle line p.
Centre of the intersection hyperbola is the centre of the line segment AB.
Ground views of points A, B are major vertices of the intersection hyperbola ground view.
Front views of these points are extremal points with respect to the ground image plane,
one is in the highest position on one branch
and the other one in the lowest position on the other branch of the intersection hyperbola (if A, BÎ1s),
or they are points located on the front view of the intersection hyperbola diameter parallel to the axis x (if A, BÎp).
Other points on the intersection hyperbola can be found on the parallel circles of the hyperboloid of revolution,
which are located in the ground image plane p
and plane parallel to p in the same distance from the basic hyperbola centre as p .
Visible and nonvisible parts of the intersection front view are separated by intersection points with the principle meridian.
Visibility of the intersection ground view changes
in the intersection points with the neck circle on the one- sheet hyperboloid of revolution,
while on the hyperboloid of two sheets that branch of hyperbola is visible,
which is located on the upper sheet of the hyperboloid of revolution.
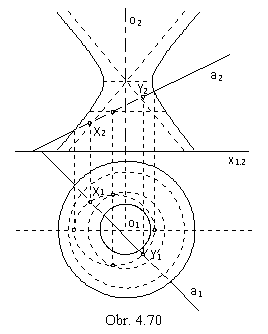
Intersection points of then line a
and one-sheet hyperboloid of revolution
determined by the axis o parallel to the frontal image plane
and principle meridian hyperbola m
can be found in the frontal projecting plane of the given line a,
which intersects the hyperboloid of revolution in the ellipse.
Front view of the intersection ellipse,
located on the illustrated patch of one-sheet hyperboloid of revolution,
is a line segment.
Ground view of the intersection
can be constructed as in the Fig. 4. 63.