SURFACES of REVOLUTION

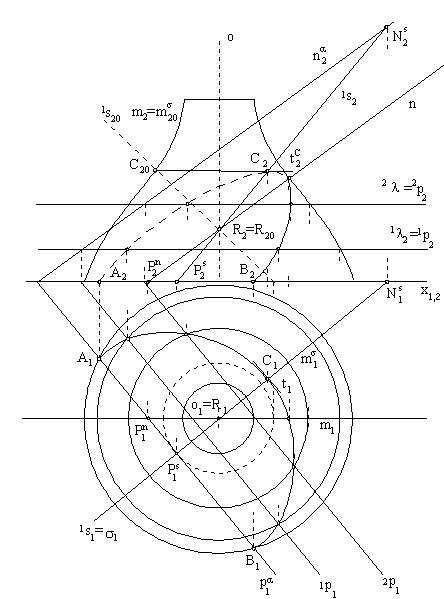
Surface of revolution cam be created by revolving a curve segment about the given axis. Axis of revolution o is an arbitrary line in the space. Geometric transformations (revolution and transaltion) can be used to locate the line o to one of the coordinate axes, or to the position parallel to one coordinate axis. In the Fig. 4. 41 the line o is translated in the direction of vector a=PO to the line o´ passing through the origin of the coordinate system, then it is revolved by angle a x aboot the coordinate axis x to the line o´´ and at last it is revolved about the coordinate axis y by the angle a y to the cooridnate axis z. Matrix of the revolution about the arbitrary line o is the product of the multiplication of matrices representing separate geometric transformations, matrix of translation and matrices of revolutions about the related coordinate axes x, y, z. In the orthographic views of the surface of revolution it is covinient to locate the axis of revolution to the line parallel to the coordiante axis z (in the Monge method) or directly to the coordinate axis z (in the orthogonal axonometry), Fig. 4. 43.
Synthetic representation: (k, TOz(v))
Analytic representations:
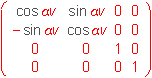 , vÎ<0,1>
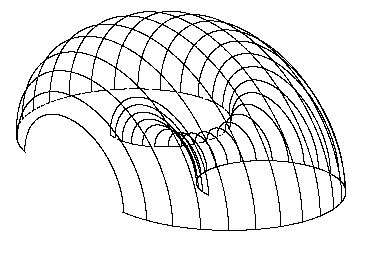
, vÎ<0,1> Surface of revolution with the axis in the axis x, which is created by revolving the Archimedean spiral
by angles from the interval <0, p> is illustrated in the Fig. 4. 42.
1. Parametric net of curves on the surface of revolution
 Net of parametric curves on the surface of revolution
Net of parametric curves on the surface of revolution
is created by u-curves congruent to the basic curve k
(separate position of the basic curve k in the revolving about the axis o)
and v-curves, trajectories of the points on the basic curve k,
parallel circles (located in planes perpendicular to the axis o).
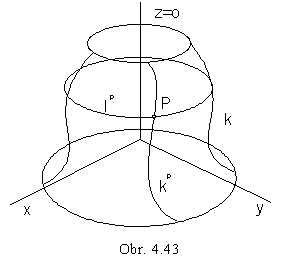
In any point P on the surface
there is located one parallel circle lP
and one revolved position of the basic curve kP (Fig. 4. 43).
Plane m passing through the axis of the surface of revolution is called the meridian plane. It is the plane of symmetry of the surface. Any surface of revolution has the infinite number of planes of symmetry, any patch of the surface of revolution at least one. Planar intersection of the surface of revolution and plane m is called meridian. It is a plane curve (a pair of plane curves) symmetric with respect to the axis of the surface of revolution. By revolution of the meridian about the axis of the surface, the same surface of revolution can be created, which was determined by the revolution of the basic space curve k. Substituting the plane meridian m instead of the space basic curve k in the creative representation of the surface of revolution, all parametric v-curves on the surface become the plane meridians
(k, TOz(v))=(m, TOz(v))
In any point P on the surface there is located one parallel circle PÎlP and one meridian PÎmP (Fig. 4. 44).
Tangent plane in the point P to the surface is determined by tangents to these curves, t = lt mt.
Meridian plane parallel to the frontal image plane is called principle meridian plane
and intersection of the surface of revolution by this plane is called principle meridian.
Tangent mt in the point P to the meridian curve is parallel to the axis of the surface of revolution, or it intersects the axis in the real point. Tangents to all meridians in the points located on one parallel circle l are lines on the tangent conical (or cylindrical) surface of revolution, which is created by the revolution of the tangent mt about the axis o (Fig. 4. 45).

Vertex V of the tangent conical surface is located on the axis of revolution.
Normals to the surface of revolution in points located on one parallel circle l are located on the normal conical surface of revolution with the axis in the axis of revolution and vertex W on the axis of revolution, while lines on this surface are perpendicular to the lines on the tangent conical surface.
Tangent cylindrical surface is tangent to the surface of revolution in the parallel circle, in the points of which there exist common tangent planes to both surfaces parallel to the axis o of the surface of revolution. Normals to the surface of revolution in the points of this parallel circle form the plane perpendicular to the axis of revolution.
Parallel circle is called the neck circle, if tangent planes to the surface of revolution in the points on this circle are parallel to the axis of revolution and the tangent cylindrical surface is located inside the surface of revolution.
Parallel circle is called the equator circle, if tangent planes to the surface of revolution in the points on this circle are parallel to the axis of revolution and the tangent cylindrical surface is located outside the surface of revolution.
Parallel circle is called the crater circle, if tangent plane to the surface of revolution in the points on this circle is perpendicular to the axis of revolution (circle is the set of parabolic points on the surface) and normal to the surface of revolution in the points of this parallel circle are parallel to the axis of revolution and form the normal cylindrical surface.
2. Views of the surface of revolution
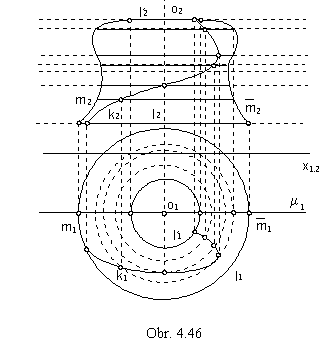 Under the Monge method, we usually project surfaces of revolution in the position of the surface axis parallel to the coordinate axis z. Ground view of the surface of revolution appears as the part of the plane inbetween two concentric circles, which are views of the surface parallel circles of the extremal radii (minimal and maximal), Fig. 4. 46. All parallel circles have their ground views in the circles with the centres in one point, which is the ground view of the axis of revolution. Front views of these circles are line segments perpendicular to the view of the axis of revolution, parallel to the coordinate axis x1,2. Front view of the surface of revolution has the outline in the view of the principle meridian located in the plane m // n, or also in the pair of line segments. These are front views of parallel circles located in the planes perpendicular to the axis of revolution and parallel to the ground image plane in the extremal distances. Principal meridian can be constructed as the set of points. Any parallel circle intersects principal meridian in two points, which are projected in the front view to the end points of the line segment - front view of the parallel circle. Front views of these intersection points are located on the front view of the parallel circle plane (parallel to the ground image plane), which is the line parallel to the axis x1,2.
Under the Monge method, we usually project surfaces of revolution in the position of the surface axis parallel to the coordinate axis z. Ground view of the surface of revolution appears as the part of the plane inbetween two concentric circles, which are views of the surface parallel circles of the extremal radii (minimal and maximal), Fig. 4. 46. All parallel circles have their ground views in the circles with the centres in one point, which is the ground view of the axis of revolution. Front views of these circles are line segments perpendicular to the view of the axis of revolution, parallel to the coordinate axis x1,2. Front view of the surface of revolution has the outline in the view of the principle meridian located in the plane m // n, or also in the pair of line segments. These are front views of parallel circles located in the planes perpendicular to the axis of revolution and parallel to the ground image plane in the extremal distances. Principal meridian can be constructed as the set of points. Any parallel circle intersects principal meridian in two points, which are projected in the front view to the end points of the line segment - front view of the parallel circle. Front views of these intersection points are located on the front view of the parallel circle plane (parallel to the ground image plane), which is the line parallel to the axis x1,2.
3. Point on the surface of revolution and tangent plane to the surface in this point
In any point T on the surface of revolution
there is located the parallel circle k
(intersection of the surface and the plane pT perpendicular to the axis of revolution o)
and the meridian mT
(intersection of the surface and the meridian plane mT passing through the axis of revolution o), Fig. 4. 48.
Tangent plane t to the surface in the point T
is determined by tangents kt and mt to the circle k and to the meridian mT in their common point T.
Ground view of the tangent kt is the tangent to the ground view of the parallel circle,
front view is a line parallel to the axis x1,2 ( kt
![]() pT).
pT).
Ground view of the tangent to the meridian mT is in the ground view of the rmeridian plane mT.
In the construction of its front view we will use the conical tangent with the vertex V on the axis od revolution o,
which can be found as the intersection point with the tangent to the principle meridian in the point on the parallel circle k.
Point T revolves on this circle to the point T 0 on the principle meridian, which appears in the front view in the true size.
Tangent mt 0 in the point T 0 intersects the axis of revolution in the vertex V of the tangent conical surface.
Tangent lines to all meridians on the surface of revolution in the points on the parallel circle k
are passing through the point V , and therefore m t=VT.
Tangent kt is the principle line of the first frame in the plane t, tangent mt is the slope line of the first frame.
Normal to the surface, perpendicular to the tangent plane,
is projected in the ground view to the line perpendicular to the view of the tangent kt.
Front view can be constructed from the normal conical surface.
Vertex W on the axis of revolution o is the intersection point of the normal n 0 in the point T 0 on the principal meridian,
the right angle of the normal n 0 and the tangent mt 0 appears in the front view in the true size.
Normal n is determined by points W and T.

4. Intersection points of line and surface of revolution
Frontal projecting plane c of the given line a perpendicular to the frontal image plane can be used for the construction. Intersection points of the line a and the curve, in which the plane c intersects the surface of revolution, are the intersection points of the line and the surface, a ÇF={Q, R}. Ground view of the intersection curve can be constructed as the set of points located in the plane c , on principle lines of the first frame. Front view is a line segment coinciding with the front view of the line a. Intersection points can be reached in the ground view. Visibility of the line with respect to the surface of revolution can be attached according to the visibility of the intersection curve (in the ground view) and with respect to the position of the intersection points and the principle meridian (in the front view), Fig. 4. 50.
5. Planar intersection of the surface of revolution and tangent line to the intersection curve in one point
Planar intersection of the surface of revolution by the plane a is the curve symmetric with respect to the line 1s, which is the intersection line of the intersection plane and the plane of symmetry s of the surface perpendicular to the intersection plane.
Intersection points of the line 1s and the surface are points on the intersection curve located in the minimal and maximal distance from the ground image plane p. They can be constructed as intersection points of the line 1s and the meridian ms ,
in which the plane s intersects the surface. Meridian ms is congruent to the principle meridian m, which is projected in the front plane in the true size. Revolving the meridian ms and line 1s in the plane s to the plane m of the principle meridian the extremal points can be determined in the front views. All other points on the intersection curve can be determined as intersection points of parallel circles on the surface of revolution in the planes il // p with the principle lines of the first frame ip in the intersection plane a, in which planes il intersect the plane a, Fig. 4. 49). Tangent line to the intersection curve in the point L is the intersection line of the intersection plane and the tangent plane t to the surface in the given point L . It is determined by tangents to the parallel circle and meridian, which are located on the surface in the point L, t= rt mt.