DEVELOPABLE SURFACES - TORSES

The line surface, to which there exists a unique tangent plane in any line located on the surface,
while the surface is located in the neighbourhood of this line
in one halfspace determined by the tagent plane ,
is the developable surface.

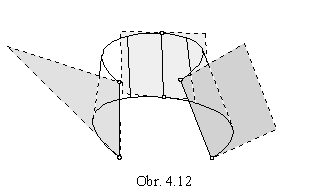
All points located on the developable surface are parabolic points (Fig. 4. 12).

Developable surfaces are:

a) plane

b) cylindrical surface

c) conical surface

d) surface of tangents to a curve

e) surface composed from patches of types a) - d) (transition surface).

I. Special types of developable surfaces

1. Cylindrical surface

Translating the curve segment k in the direction of the non-zero translation vector a cylindrical surface can be created
(Fig. 4. 13).

Synthetic representation:     (k, T_P(v) )

Analytic representations:

basic figure -          r(u)=(x(u), y(u), z(u), 1), uÎ<0,1>

generating principle -      class of translations determined by the vector

a = (a₁, a₂, a₃, 0), a 0

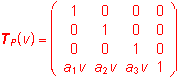    , vÎ<0,1>

modelled figure - p(u,v)=r(u).T_P(v)=(x(u)+a₁v, y(u)+a₂v, z(u)+a₃v, 1), (u,v)Î<0,1>²

If the basic curve segment k is a plane segment, k a and vector a is the direction vector of the plane a,
the created surface patch is the part of the plane a (Fig. 4. 14).

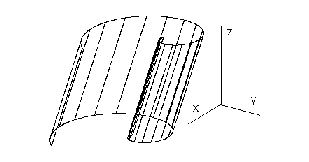
                              Fig. 4. 14                                                            Fig. 4. 15

If the basic curve segment k is the circle in the plane a
and vector a is not the direction vector of the plane a, a x a,
the patch of the cylindrical surface can be created,
for the direction vector a^a it is a patch of the cylindrical surface of revolution.
Illustration of the cylindrical surface patch with the basic curve in the Archimedean spiral is in the Fig. 4. 15.
If the basic curve segment is the polygon
and vector a is not parallel to any of the polygon sides,
modelled surface patch is the part of the prismatic surface
                             Fig. 4. 16                          with the edges in the direction of vector a (surface created by planar patches).

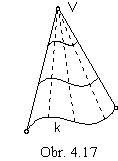
2. Conical surface

From the basic curve segment k a conical surface patch can be created by scalings to the given real point- centre V
with a non-zero coefficient h (Fig. 4. 17).

Synthetic representation:      (k, T_R(v) )

Analytic representations:

basic figure -      r(u)=(x(u), y(u), z(u), 1), uÎ<0, 1>

generating principle -      class of scalings to the centre V=(x_v, y_v, z_v, 1)

with the coefficient h 0

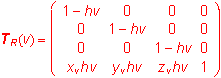, vÎ<0, 1>

modelled figure -

     p(u, v)=r(u).T_R(v)=((1-hv) x(u)+x_v hv, (1-hv) y(u)+y_v hv, (1-hv) z(u)+z_v hv,1), (u, v)Î<0,1>²

Non-zero coefficient hof the scalings determines the surface patch form:



h>1 conical surface patch of two sheets


h=1 conical surface patch with the vertex V


0<h<1 frustum of the conical surface patch inbetween the basic curve segment k and vertex V


h<0 frustum of the conical surface patch in the opposite direction from the basic curve segment k than vertex V

               Fig. 4. 18

If the basic curve segment k is a plane segment in the plane a ans in this plane also vertex V is located,
the created surface patch is a part of the plane a (Fig. 4. 18, coefficient h<1).
If the basic curve segment k is a circle in the plane a and centre V is not located in the plane a,
the created surface patch is the circular conical surface patch with the vertex V.
If the line passing through the point V perpendicularly to the plane a
intersects this plane in the centres of the basic circle k,
the created conical surface patch is the surface of revolution.
Illustration of the conical surface patch
with the basic curve in the Folium of Descartes is in the Fig. 4.19, coefficient h>1.
If the basic curve segment is the polygon k and centre V is not the point of this line,
modelled surface patch is the pyramidal surface patch with the vertex in the point V
(surface composed from planar patches) (Fig. 4. 20, coefficient h=1).

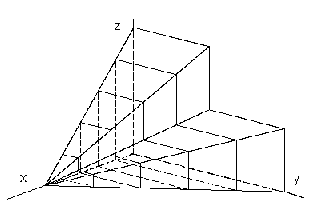
                    Fig. 4. 19                                                                  Fig. 4. 20

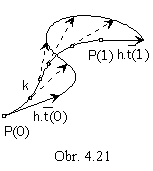
3. Surface of tangents to a curve

Translating points on basic curve segment in the direction of tangent vectors to the basic curve segment in these points the surface of tangent lines to a curve can be created( Fig. 4. 21).

Synthetic representation:      (k, T_T(u, v) )

Analytic representations:

basic figure -      r(u)=(x(u), y(u), z(u), 1) , uÎ<0, 1>

generating principle -      class of translations determined by vector

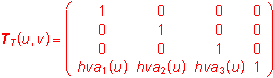, (u,v)Î<0,1>², h 0

modelled figure - p(u, v)=r(u).T_T(u,v)= (x(u)+hva₁(u), y(u)+hva₂(u), z(u)+hva₃(u), 1), (u, v)Î<0,1>²



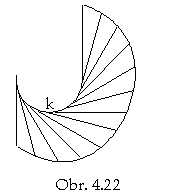
If the basic curve segment k is a planar segment, k a,
tanget vector r´(u) at any point on the curve segment
is the direction vector of the plane a
and the modelled surface patch is a part of the plane a (Fig. 4. 22).

For the space basic curve segment
tangent vectors are non-collinear and non-complanar vectors (Fig. 4. 23).

If the basic curve segment is a helix,
the only one developable helical surface can be created,
surface of tangent lines to the helix (Fig. 4. 24).

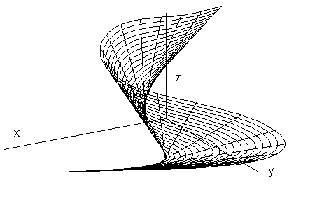
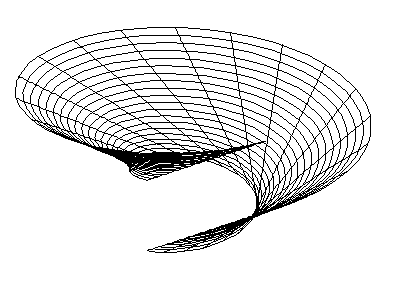
                      Fig.4. 23                                                                           Fig. 4. 24

4. General developable line surface

The line surface can be determined by two basic curves (u-parametric curves on the surface),
while any line located on the surface (v-parametric curve)
is passing through one point on each of the basic curves.
For the suitably chosen pairs of corresponding points on basic curves only,
(suitable parametrisation of point functions, which are analytic representatins of basic curves)
we can create the developable surface.
Generating principle in the synthetic representation of the general developable surface
is a linear interpolation (Fig.4. 25).

Synthetic representation:    ({¹k,²k}, I(v) )

Analytic representations:     ¹r(u)=(¹x(u), ¹y(u), ¹z(u), 1),
                                           ²r(u)=(²x(u), ²y(u), ²z(u), 1),     uÎ<0, 1>

map of the surface patch   M=( ¹r(u), ²r(u) )

generating principle - linear interpolation     I(v)=(1-v    v)

modelled figure

    p(u, v)=M . I^T(v) = ( ¹x(u)(1-v) + ²x(u)v, ¹y(u)(1-v) + ²y(u)v, ¹z(u)(1-v) + ²z(u)v, 1), (u, v)Î<0,1>²

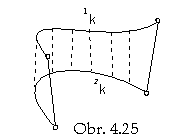
Cylindrical surface can be created from two congruent basic curves ¹k and ²k, while one of them was created by the translation of the other one. Translation vector determines the direction of lines on the cylindrical surface.
For conical surface and surface of tangent lines to a curve are these two curves ¹k and ²k homothetical (Fig. 4. 26),
or one of them is represented by a constant point function, it is a point - vertex of the conical surface.
Transition surface patch (type e.) determined by an ellipse and a closed polygon is in the Fig. 4. 27, it is created by four different triangles (parts of surface tangent planes) and four different conical patches with vertices in the vertices of the basic polygon and boundary line segments in the sides of the separate triangles.

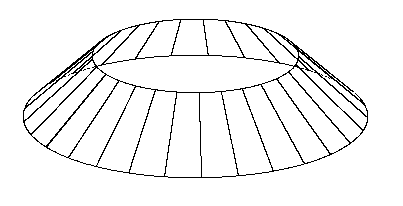
                                                         Fig. 4. 26                                      Fig. 4. 27

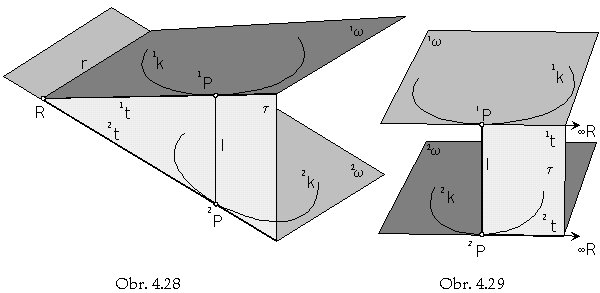
Line on the developable surface can be determined by the tangent plane to the surface in this line.
Curve ¹k has in the point ¹P osculating plane ¹w, in which the tangent line ¹t to the curve in the point ¹P is located.
Tangent line ¹t is also located in the tangent plane t to the surface
(t is the set of tangent lines to all curves located on the surface in the given point).
Point ²P on the curve ²k , which determines with the point ¹P the line l=¹P ²P on the surface
can be constructed as the tangent point on the tangent line ²t to the curve ²k,
located in the osculating plane ²w and also in the tangent plane t.
Lines ¹t, ²t are intersection lines of the plane t and osculating planes ¹w, ²w
and they can have only a non-empty intersection, common real or ideal point.
Their superposition determines the position of osculating planes ¹w, ²w.

¹w Ç ²w = r         ¹t Ç ²t = R,     RÎr     (Fig. 4. 28)

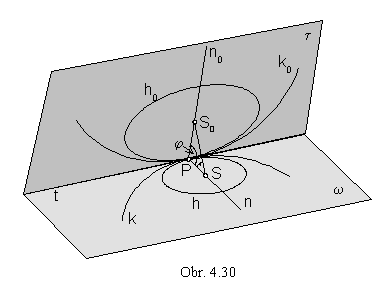
¹w Ç ²w = r        ¹t Ç ²t = R     (Fig. 4. 29)

II. Developement of the surface

Developable line surface is the envelope of the space between two basic curves ¹k, ²k created by tangent planes.
Development of the surface is the isometric mapping of the surface to the plane, for which the following rules are valid:

1. Length of curve segments on surface is invariant

2. Size of angles formed by curves on surface is invariant

3. Catalano theorem: radius of the first curvature of the curve on the surface and the radius of the first curvature of its development to the plane are in all points determined by the ratio , where j is the angle of the osculating plane w of the curve in the given point and the tangent plane t, to which is the curve developed, (Fig. 4. 30).

Triangle PSS₀ has a right angle in the vertex S - centre of the first curvature in the point P on the curve k located in the plane w. Leg PS of the triangle PSS₀ has the lenght equal to the radius of the first curvature ¹r of the curve and it forms the angle j with the hypotenuse PS₀ from the plane t. Lenght of the hypotenuse is equal to the radius of the first curvature ¹r₀ in the point P on the curve k₀ developed to the plane t.
Points S, S₀ are centres of osculating circles h, h₀
of curves k, k₀ in the common point P,
their radii are the radii of the first cuvatures ¹r, ¹r₀.

t x w=t     t w = j      SS₀^a

For j = 0 ⁰ is the curve k developed to its osculating plane in the given point P,
to the plane curve k₀ with the same radius of the first curvature ¹r = ¹r₀ .

For j = 90⁰ is the curve k developed to its tangent t located in the tangent plane t
perpendicular to the osculating plane w in the point P with the radius of the first curvature ¹r ₀ = .

Patch of the developable line surface can be developed to one from its tangent planes t,
which is tangent to the surface in one line

l=¹P ²P, ¹Pιk, ²Pβk.

Let the curves ¹k, ²k be plane curves located in the osculating planes ¹w, ²w.

For the development we must satisfy the following rules:

1. Length of the line segments on the surface lines is preserved invariant     d = | ¹P ²P |

2. Size of angles of basic curves with the surface lines is preserved invariant

    ¹a = | ¹k l | = | 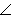¹t l |     ²a = | ²k l | = | 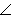²t l |

3. Catalano theorem

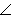¹j = ¹w t    ¹r₀= ¹r cos ¹j    ²j = 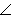²w t     ²r₀ = ²r cos ²j

¹r ₀ , ²r₀ are radii of the first curvatures of developed curves ¹k₀, ²k₀ to the tangent plane t in points ¹P, ²P.
On normals to these curves (perpendicular to tangents ¹t, ²t) there are located centres of curvatures ¹S, ²S,
which are centres of osculating circles in the given points, ¹h(¹S, ¹r₀), ²h(²S, ²r₀).

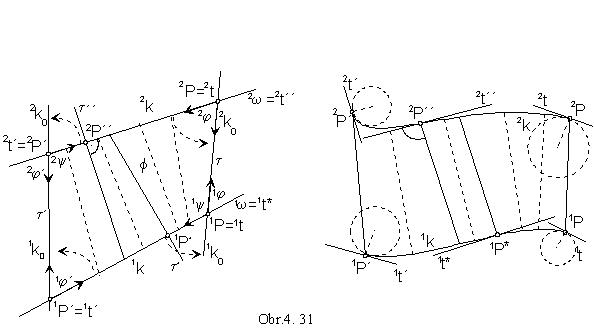
  Developed curve can be in the given point (Fig. 4. 31):

a) concave and located in the same halfplane determined by tangent as the developed surface patch F
curve segment ²k in the neighbourhood of the point ²P
- angle ²j of planes ²w and t is equal to the angle of halfplanes (²t ²P´) ²w and (²t ¹P) t
enveloping the surface patch F

b) concave and located in the opposite halfplane determined by tangent as the developed surface patch F
curve segment ¹k in the neighbourhood of the point ¹P
- angle ¹j of planes ¹w and t is complement to the angle ¹y of halfplanes (¹t ¹P´) ¹w and (¹t ²P) t
enveloping the surface patch F, ¹j + ¹y = p

c) convex and located in the same halfplane determined by tangent as the developed surface patch F
curve segment ¹k in the neighbourhood of the point ¹P´
- angle ¹j´ of planes ¹w and t´ is equal to the angle of halfplanes (¹t´ ¹P) ¹w and (¹t´ ²P´) t´
enveloping the surface patch F

d) convex and located in the opposite halfplane determined by tangent as the developed surface patch F
curve segment ²k in the neighbourhood of the point ²P´
- angle ²j´ of planes ²w and t´ is complement to the angle ²y of halfplanes (²t´ ²P) ²w and (²t´ ¹P´) t´
enveloping the surface patch F, ²j´ + ²y = p

e) intersecting the tangent ( in the point of inflection)
curve segment ²k in the point ²P´´, curve segment ¹k in the point ¹P^*
- angle ¹j = ²j = p/2, ¹w^t*, ²w^t´´.

For the surface of tangents to the space curve the osculating plane w in all points P on the basic curve
coincide with the tangent plane to the surface, w=t, j= 0⁰ and ¹r=¹r₀.
Curve k is developed to the plane curve k₀, while the first curvatures of the curves ¹k, ¹k₀ are equal in all points
(surfaces in Fig. 4. 23, 4. 24).

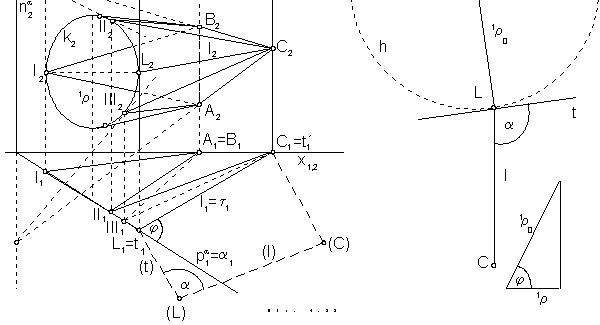
Problem: Find one line l located on the transition surface determined by:

a) circle k in the ground image plane and circle k´ in the frontal image plane,

b) circle k in the plane a perpendicular to the frontal plane and polygon ABC in the frontal plane.

Determine radii of the first curvatures ¹r and ¹r´ of developed circles to the tangent plane t in the surface line l .

Solution:

a) Tangent plane t in the seeked line l located on the transition surface is determined by tangents to the basic circles, which are its traces in the image planes (Fig. 4. 32). Angles a, a´ of tangents t, t´ and line l=LL´ (L, L´ are tangent points on basic circles) on the surface and the lenght of the line segment |LL´|=d can be determined
by revolution of the tangent plane t about tangent t´ (trace in the frontal plane) to the frontal image plane.
By lowering the slope lines ¹s and ²s, angles ¹j = t p , and ²j = t n
of osculating planes (ground image plane p and frontal image plane n) and tangent plane t, to which the surface,
and therefore the circles k and k ´ are developed, can be determined.
Lenght of the radii of the first curvatures ¹r₀ and ¹r₀´ of developed curves
can be constructed by the Catalano theorem,
from the radii of the first curvatures of circles, which are equal to the radii ¹r and ¹r´ of the circles.

.

b) Transition surface is composed from three different conical surface patches and three triangles,
which are parts of tangent planes to the surface in the boundary line segments on the conical patches (Fig. 4. 33).
Vertices I, II and III of these triangles located on the circle k ,
can be determined as tangent points of those tangents to the circle k,
which intersect with lines in the sides of the basic polygon ABC on the trace of the plane a in the frontal plane
(these tangents are intersection lines of the osculating plane a of the circle k
and tangent planes to the transition surface in the sides of the basic polygon ABC,
while in these sides there are located their traces in the frontal plane).

Line on the transition surface located in the point LÎk can be determined similarly:
tangent t in the point L to the circle k intersects the trace n^a in the point,
through which line t´ determined by one vertex of the basic polygon ABC - vertex B is passing.
Line l=LB is located on the conical patch I BIII, which is a part of the created transition surface.
Lines t, t´ determine tangent plane t to the transition surface,
to which the circle k in the neighbourhood of the point L will be developed,
to the curve with the radius of the first curvature ¹r ₀ .
Its size can be constructed from the triangle in the Catalano theorem.
Radius of the first curvature equals to the radius ¹r of the circle k.
Angle j, which the osculating plane a of the circle k forms with the tangent plane t
equals to the angle of lines, which are first views of planes t and a.