c
Analytic representation of the surface is a point function
I. Definition and intrinsic properties of surfaces
Definition: Surface (surface patch) c is any connected non-empty subset of the extended Euclidean space,
c
![]()
![]() , which is a continuous mapping of the connected region W
, which is a continuous mapping of the connected region W
![]() R2.
R2.
Analytic representation of the surface is a point function
p(u,v)=(x(u,v), y(u,v), z(u,v), h(u,v))
defined, continuous and at least once differentiable on W.
Value of the point function for (a,b)ÎW is the point on the surface determined by
the quadruple of homogeneous coordinates
P(a,b)=p(a,b)=(x(a,b), y(a,b), z(a,b), h(a,b))
Numbers (a,b)ÎW are called parametric - curvilineare coordinates of the surface point.
For real points on the surface h(a,b)
![]() 0.
If the region W is a regular region, we speak about surface patch.
0.
If the region W is a regular region, we speak about surface patch.
In the computer processing, the parametrisation of the surface is usually chosen on the region W=<0,1>2
and we speak about the surface patch over the unit square.
Point function defines the orientation of the surface patch c.
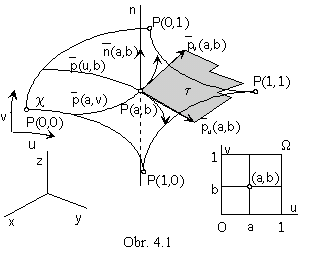 Points on the surface patch,
Points on the surface patch,
with the curvilinear coordinates equal to 0 or 1,
are denoted as corner points of the surface patch
P(0,0), P(1,0), P(0,1), P(1,1).
For constant values of one variable u=a, or v=b, we receive from the point function of two variables the point function of one variable determining the curve located on the surface, which is called parametric v-curve, or u-curve. Parametric curves form two systems of curves located on the surface. Each curve from one system intersects all curves from the other system. Two parametric curves from different systems have a common point located on the surface, curvilinear coordinates of this point are coresponding constant values of parameters u and v
p(a,v)Çp(u,b)=p(a,b)=P(a,b)
Parametric curve segments located on the surface patch with constant values of variables u and v equal to 0 or 1,
are called boundary curve segments of the surface patch.
Surface patch boundary curve segments from different parametric systems intersect in the patch corner points, Fig. 4. 1.
Partial derivative of the point function p(u,v) is the vector function
![]() , or
, or ![]()
determining for u=a, or v=b the tangent vector to the parametric u-curve, or v-curve in the point P(a,b),
denoted as pu(a,b), or pv(a,b).
Point on the surface, in which any from the partial derivatives pu(a,b), or pv(a,b) of the surface point function is the zero vector, or these two vectors are linearly dependent, is called the singular point.
In the regular point P(a,b), there are tangent vectors to the parametric curves non-zero and linearly independent,
they define a unique tangent plane t to the surface in the regular point.
Tangent plane t in the regular point P(a,b) to the surface containes tangent lines to all curves located on the surface and passing through the tangent point.
Vector
n(a,b)=pu(a,b)´pv(a,b)
Is called normal vector to the surface in the regular point P(a,b).
It is perpendicular to the tangent plane and in the case of the positive orientation of the surface it is oriented to the opposite halfspace from the tangent plane than the surface.
Line determined by the normal vector and passing through the point P(a,b) is called normal to the surface. Normal to the surface is perpendicular to tangent lines to all curves located on the surface and passing through the point P(a,b), which are located in the tangent plane t.
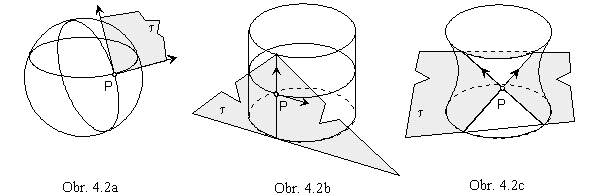
Point on the surface is called elliptic point , if the tangent plane to the surface in this point does not contain any other point of the surface in the neighbourhood of the tangent point. This neigbourhood on the surface is located in one halspace determined by the tangent plane (Fig. 4. 2 a). All points on the sphere or on the ellipsoid are elliptic points.
Point on the surface is called parabolic point , if the tangent plane to the surface in this point contains a curve located on the surface, it is tangent to the surface in this curve (or it ntersects the surface in the curve, while the tangent point is the cuspidal point on the tangent curve). Neighbourhood of the tangent curve on the surface is located in one halfspace determined by the tangent plane (Fig. 4. 2 b). All points on the cylindrical or the conical surface are parabolic points.
Point on the surface is called hyperbolic point , if the tangent plane to the surface in this point intersects the surface in the intersection curve, while the tagent point is the double point on the intersection curve. Surface is located in both halfspaces determined by the tangent plane (Fig. 4. 2 c). All points on the hyperboloid are hyperbolic points.
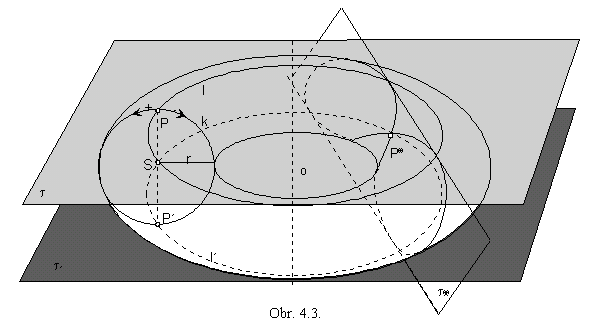
Torus is the surface, on which all types of points are located (Fig. 4. 3).
It can be created by revolving a basic circle k(S, r ) about the axis, which is located in the plane of the basic circle.
All points on circles l and l´, created by revolutions of the points P and P´ from the basic circle k about the axis of revolution o (and located in the same distance from the axis o as the centre S of the basic circle k), are parabolic points.
Tangent planes t and t´ are perpendicular to the axis o and they are tangent to the torus in the circles l and l´.
All points on the torus, created by revolution of the circular arc PP´ (clockwise oriented) are elliptic points, tangent planes to the torus in these points have no more common points with the torus, but the tangent point.
All points on the torus, created by revolution of the circular arc PP´ (anti-clockwise oriented) are hyperbolic points, tangent planes to the torus in these points intersect torus in the curve with the double point in the tangent point.
Vector
puv(a,b) =
![]()
of the mixed second partial derivative of the surface point function
is called twist vector to the surface in the regular point P(a,b).
It represents the "curvature" of the surface in the neighbourhood of the given point.
Point, in which the twist vector is a zero vector, puv(a,b) = 0, is the point of inflection,
surface is in the neighbourhood of this point a part of the plane.
II. Problems on surfaces
1. Views of surfaces
2. Point on the surface - tangent plane to the surface - normal to the surface


3. Curve on the surface - tangent line in the given point
 t
t 4. Planar intersection of the surface - tangent line to the intersection in the given point
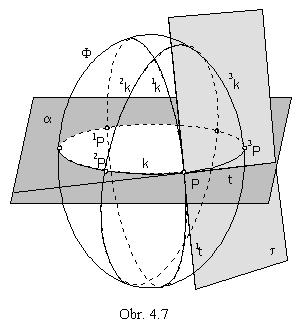
 a, t
a, t
 t , then t=a Ç t
t , then t=a Ç t 5. Intersection points of a line and surface
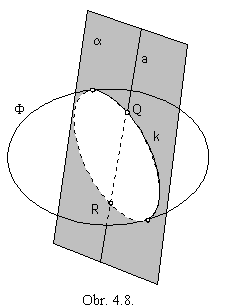
 a
a 6. Intersection of surfaces
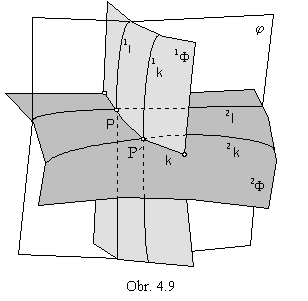
 1F, 2l
1F, 2l
 2F, 1l Ç 2l =P,
2F, 1l Ç 2l =P, 7. Regular mappings of surfaces
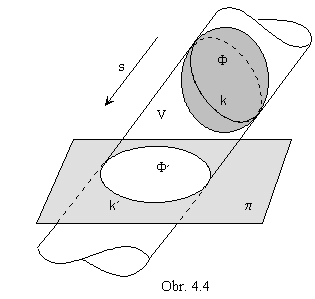
Regular mapping of the surface 1F to the surface 2F is calles development (isometric mapping), if it preserves invariant the length of curve segments on surfaces (Fig. 4. 10).
1F® 2F, 1A1B
![]() 1k ® 2A2B
1k ® 2A2B
 2k, |1A1B|=|2A2B|
2k, |1A1B|=|2A2B|
Surface is developable, if it can be developed to the plane.
Regular mapping of one surface to another one is called similarity (conform mapping), if it preserves the size of angles which form curve segments on surfaces (angle of two curve segments is equal to the angle of tangent lines to the curves in their common point) (Fig. 4. 11).
1F ® 2F 1k ® 2k 1l ® 2l |
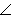 1k 1l| = |
1k 1l| = |
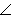 1a 1b| = |
1a 1b| = |
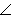 2k 2l| = |
2k 2l| = |
![]() 2a 2b|
2a 2b|
For any two surfaces 1F, 2F there exists such neighbourhood 1O of the point 1PÎ1F, for which there can be found
a neighbourhood 2O of its image 2PÎ2F, that the mapping of these neighbourhoods 1O on 2O is a conform mapping.
Some types of maps are conform mappings of the part of the Earth to the plane.
III. Modelling of surfaces
Synthetic representations of surfaces in the Creative space can be in three different types. 
Curve segment is analytically represented
by a point function of the given properties on the interval <0,1> (see Lecture 2.).
Analytic representation of the class of geometric transformations
is the matrix - function T(v) of type 4´4, defined on the interval <0,1>,
with elements of the given properties (see Lecture 2.).
Modelled surface patch is analytically represented
by a point function defined on the region W=<0,1>2
and satisfying the required properties
From the given surface patch analytically represented
by the point function q(u, v)
of the required properties on the region W there can be created a surface patch.
Applied geometric transformation is defined
by the regular square matrix T of rank four with real elements.
Modelled surface patch can be congruent to the basic one (in metric transformations),
or it can be an affine, or a projective image of the basic figure.
Point function of the required properties
defined on the region W and representing the surface analytically is in the from
Map M of the modelled surface patch - analytic representation of the basic figure
is the matrix of type n´m,
its elements are analytic representations of the elements of the basic figure,
quadruples of the homogeneous coordinates of points,
or point functions of curve segments.
Approximation or interpolation are analytically represented
by matrices I(u) ans I(v) of types 1´n and 1´m,
with elements in the form of the polynomial functions Pli(u) of degree n-1
and Pli(v) of degree m-1 satisfying the given conditions.
Interpolation surface patch is analytically represented
by a point function
defined and satisfying the required properties on the region W=<0,1>2.