CURVES in the SPACE
1. Cylindrical helix
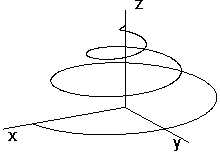
Cylindrical helical movement is the class of geometric transformations composed from the class of revolutions about the axis o and the class of translations in the direction of the vector collinear to the axis of revolution o.
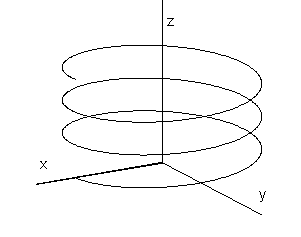
Synthetic representation: (A, TS(u))
Analytic representation:
basic figure - A=(a, 0, 0, 1)
generating principle - cylindrical helical movement
about the coordinate axis z
determined by the translation vector
a=(0, 0, v0, 0 ) in the direction of the axis z
 , uÎ<0,1>
, uÎ<0,1>
r(u)=A. TS(u)=(acos au, asin au, av0u,1)
uÎ<0,1>, a
 0 is the radius of the helix, axis of revolution o=z is the axis of the helix
0 is the radius of the helix, axis of revolution o=z is the axis of the helix
a=2p for one pitch of the helix (in the clockwise (Fig. 3.24), or anti-clockwise direction,
with respect to the orientation of the angle of revolution a),
a=2kp , k
 0 for k pitches
0 for k pitches
v0 is the reduced pitch, vz is the pitch, vz=2pv0
Intrinsic properties of the modelled figure:
One pitch of the helix is determined by - r(u)=(acos 2pu, asin 2pu, 2pv0u,1)
r´(u)=2p(-asin 2pu, acos 2pu, v0, 0) ç r´(u)ç = 2p
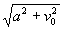 =2pd
=2pd
r´´(u)= -4p2(acos 2pu, asin 2pu, 0, 0) r´´´(u)= -8p3a(-sin 2pu, cos 2pu, 0, 0)
[r´(u) r´´(u) r´´´(u)]=64p6a2 v0
r´(u) ´ r´´(u)= 8p3a(v0 sin 2pu, -v0 cos 2pu, a, 0) ç r´(u) ´ r´´(u)ç = 8p3ad
Frenet-Serret trihedron in the point P(u), uÎ<0,1>
t(u)=(-asin 2pu, acos 2pu, v0, 0)/d b(u)= (v0 sin 2pu, -v0 cos 2pu, a, 0)/d
n(u)= (cos 2pu, sin 2pu, 0, 0)
1k(u)=a/d2 1r(u)=d2/a 2k(u)=v0/d2
Rectification of the length of one pitch of the cylindrical helix (Fig. 3.25)

One pitch of the helix is developed to the hypotenuse of the right-angled triangle. Legs of the triangle are of the legth equal to the pitch vz and the circumference 2pa of the cylindrical surface of revolution on which is the helix vinded.
Angle j, that form all tangents to the helix with the plane perpendicular to the axis of the helical movement,
is called slope of the helixe. Helix is the curve of the constant slope.
Direction conical surface to the helix is the conical surface of revolution, lines of which are parallel to the tangents to the helix, vertex is ther point W on the axis of the helix and the basic circle with the radius a (radius of the helix) is located in the plane r perpendicular to the ais of the helix. Distance of the vertex and the plane of the basic circle equals to the reduced pitch of the helix v0=|Wr|.
Tangent planes to the direction conical surface are parallel to the helix osculating planes.
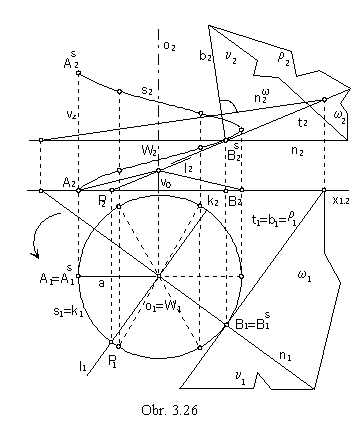
Construction of the moving Frenet - Serret trihedron in the given point BS located on the clock-wise helix is on the Fig. 3.26. Let the axis o of the helix be parallel to the coordinate axis z.
The ground view of the helix is the circle s1 with the centre in the point o1 (ground view of the helix axis o) and radius of the helix radius a. Patch of the direction conical surface to the helix is projected in the ground view to the disc with the boundary circle k1=s1 of the radius a.
Front view of the direction conical surface patch is the triangle with one vertex W2 on the axis o2 , |W2x1,2|=v0 .
Let us construct the osculating plane w in the point BS on the helix.
Rplane is determined by the tangent t to the helix in the point BS (slope line of the first frame forming the slope - angle of the plane w and the ground image plane p - slope j of the helix ) and normal n (principle line of the first plane perpendicular to the tangent).
Tangent t to the helix can be constructed with respect to the parallel line l located on the direction conical surface of the helix and passing through the vertex W.
Binormal b to the helix s is perpendicular to the osculating plane w, rectification plane r is perpendicular to the ground image plane.
2. Conical helix
Conical helical movement is a class of geometric transformations composed from the class of revolution about the axis o (axis of the movement) and a class of scalings to the centre V located on the given axis o, with the coefficient h=1.
Synthetic representation (A, TOR(u))
Analytic representations:
basic figure - A=(a, 0, 0, 1)
conical helical movement with the axis in the coordinate axis z determined by the centre V=(0, 0, vz,1) on the axis and coefficient h=1
r(u)=A.TOR(u)=((1-u)acos au, (1-u)asin au, kvzu, 1)
uÎ<0,1>, a
 0, k
0, k
 0 is the number of pitches, a=2kp
0 is the number of pitches, a=2kp
a=2p for one pitsch of the helix
Conical helix is the curve located on the coniucal surface of revolution with the axis in the axis of the conical helical movement, vertex V located on the axis of the movement and basic circle with the radius a located in the plane perpendicular to the axis of the movement.
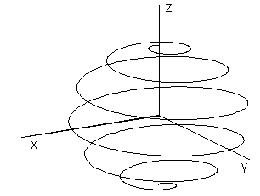
3. Spherical helix
Spherical helical movement is the class of geometric transformations composed from the two classes of revolutions about the axes 1o, 2o
 perpendicular to each other.
perpendicular to each other.
Syntetic representation: (A, T00(u))
Analytic representations:
basic figure - A=(0, 0, a,1)
generating principle - spherical helical movement with the axes
1o in the coordinate axis x
and axis 2o in the coordinate axis z, k
 0
0
 , uÎ<0,1>
, uÎ<0,1>
r(u)=A.T00(u)=(asin au sin 2kpu, -asin au cos 2kpu, acos au, 1)
uÎ<0,1>, a
 0, k
0, k
 0 is number of pitches, a=p
0 is number of pitches, a=p
Spherical helix is the curve located on the sphere with the centre in the intersection point of axes of revolutions
O=1oÇ2o and radius a=|OA|.
For the angle a=2p a k=0,5 we can create the Viviani curve with the double point (a, 0, 0, 1) on the coordinate axis x (Fig. 3. 29).
4. Viviani curve (Fig. 3.29)
Viviani curve is the space curve created by the movememnt of the point, which is the composition of two classes of revolutions about the axis 1o, 2o perpendicular to each other.
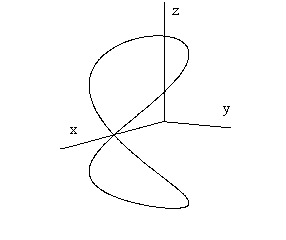
Synthetic representation: (A, T00(u))
Analytic representations:
basic figure - A=(0, a, 0, 1)
composed class of revolutions about coordinate axis x and z
 , uÎ<0,1>
, uÎ<0,1>
r(u)=A.T00(u)=(-asin 2pu cos 2pu, acos2 2pu, asin 2pu, 1) uÎ<0,1>, a
 0
0
Viviani curve is the intersection curve of the cylindrical surface of revolution
with the axis parallel to the axis of revolution 2o and radius equal to a/2
and the sphere, with the centre in the intersection point of the axes of revolutions O=1o Ç2o and radius a.
In the double point V on the curve, there is the common intersection point of the both surfaces
located on the coordinate axis y, Fig. 3.30.
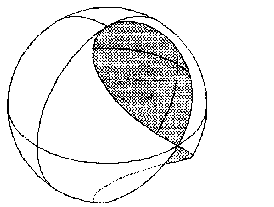
Fig. 3.30


 , uÎ<0,1>
, uÎ<0,1> 

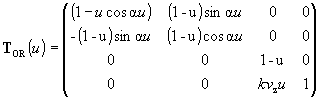
 0 is the number of pitches, a=2kp
0 is the number of pitches, a=2kp  perpendicular to each other.
perpendicular to each other.
 0
0 , uÎ<0,1>
, uÎ<0,1> 0, k
0, k
 0 is number of pitches, a=p
0 is number of pitches, a=p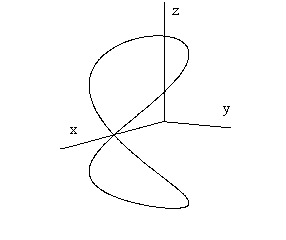
 , uÎ<0,1>
, uÎ<0,1>  0
0 