Curves in the Extended Euclidean Space
![]()
1. Definition and interior properties of curves
Definition: Curve (curve segment) is any connected non-empty subset in the space, k
![]()
![]() ,
,
which is a continuous mapping of the real interval I
![]() R. Analytic representation of the curve is a point function
R. Analytic representation of the curve is a point function
r(u)=(x(u), y(u), z(u), h(u))
defined, continuous and at least once differentiable on I.
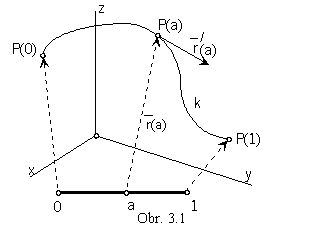
Value of the point function for aÎI is the point determined by quadruple of homogeneous coordinates
r(a)=(x(a), y(a), z(a), h(a)) = P(a)
Number aÎI is the parametric - curvilinear coordinate of the point on the curve, which defines its position on the curve (Fig. 3.1). Functions x(u), y(u), z(u), h(u) are coordinate functions.
In the case, I is a closed interval, we speak about curve segment. In the computer processing it is suitable to choose a normalised parametrisation of all curve segments on the same interval I=<0,1>, for the easy unificated denotation.
The point function defines the orientation on the curve segment k, the start point is the point with the curvilinear coordinate 0, the end point with 1. Because real points in the space only can be visualised (due to the real dimensions of the image space), used curve segments will contain only real points and the value of the coordinate function h(a) will be in the normalised form equal to constant 1 in analytic representations of all these concerned curve segments.
Point function is induced by the vector function r(u)=(x(u), y(u), z(u), 0) of one real variable defined on I, while the locus of the vector function gives the curve k. Values of the vector function are position vectors of points located on the curve,
r(a)=(x(a), y(a), z(a), 0), aÎ I.
Analytic representation of the curve - point function r(u)=(x(u), y(u), z(u), h(u)) for uÎI is equivalent to the other curve representations
If there exist real numbers a, bÎI, a
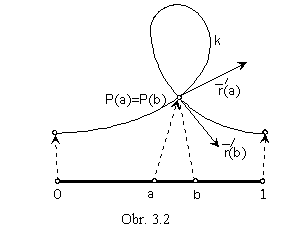
![]() b, for which it is valid r(a)= r(b), the point on the curve segment determined by the curvilinear coordinate "a" and the point determined by the curvilinear coordinate "b" coincide, and P(a)=P(b) is called the double point on the curve (Fig. 3.2).
b, for which it is valid r(a)= r(b), the point on the curve segment determined by the curvilinear coordinate "a" and the point determined by the curvilinear coordinate "b" coincide, and P(a)=P(b) is called the double point on the curve (Fig. 3.2).
If there exist n such numbers from the interval I, the point is called as the n-multiple one.
Curve segment is called the closed one, if P(0)=P(1).
The first derivative of the point function r´(u)=(x´(u), y´(u), z´(u), 0)
is the (vector) function representing for any aÎI the direction vector of the tangent line to the curve segment in the point P(a)
The orientation of the vector is equal to the orientation of the curve segment in the point P(a). Point on the curve, in which the orientation of the tangent vector turnes up, is called the cusp ( the cuspidal point).
Line, determined by the point P(a) and the direction vector r´(a) is the tangent line to the curve.
Point on the curve segment, in which the direction tangent vector is a non-zero vector, is called a regular point.
If r´(a)= 0, point P(a) is a singular point.
Point, in which the second derivative of the curve point function is a zero vector,
Properties of the curve represented in its regular points by the curve point function derivatives,
norms of vectors r´(a), r´´(a), or r´´´(a), are called intrinsic (geometric) properties.
In calculations of these properties we will use Cartesian coordinates of all points and vectors, only.
Let P(a) for aÎI be a regular point on the curve segment with the analytic representation r(u) on the interval I.
Unit tangent vector t(a) in the regular point P(a) on the curve segment can be represented by the formula
![]()
Unit binormal vector b(a) is the vector, which can be obtained as the vector product of vectors of the first and the second derivative of the point function r(u) in the regular point P(a) on the curve segment
![]()
Line determined by the point P(a) and the direction vector b(a) is the binormal.
Unit (principle) normal vector n(a) in the regular point P(a) on the curve segment is the vector product of the unit binormal and the unit tangent vectors
n(a) = b(a) ´ t(a)
Line determined by the point P(a) and the direction vector n(a) is the principle normal.
In any regular point P(a) on the curve segment there exist three perpendicular unit vectors
t(a) ^ b(a) ^ n(a) ^ t(a)
determining three perpendicular lines, t ^ b ^ n ^ t , with the common point P(a). Each two of these lines determine plane. All planes passing through the tangent t are tangent planes t to the curve segment in the point P(a).
Osculating plane w is determined by tangent and normal, w=tn.
Rectification plane r is determined by tangent and binormal, r=tb.
Normal and binormal determine normal plane n=nb.
Planes w, r and n are perpendicular to each other, they have one common point P(a)
and any two of them intersect in the common line.
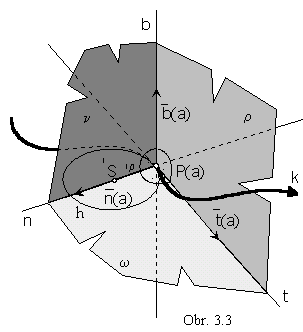
Frenet-Serret moving trihedron
in the regular point P(a) on the curve
is a geometric figure (Fig. 3.3) uniquelly determined as
the intersection of three halfspaces
with the boundary planes w, r and n,
and direction vectors b, n, t (in the given order).
Edges are halflines with the common start point
in the trihedron vertex P(a).
Curve segment in the neighbourhood of the point P(a)
is located inside the F-S trihedron,
and by its elements we can determine
intrinsic geometric properties of the curve segment
in the neighbourhood of the regular point P(a).
The elevation of the curve from its tangent in the given regular point
P(a) is represented by the first curvature - flection.
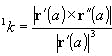
In the point of inflection on the curve, it is 1k=0. If there is 1k=0 in all regular points on the curve segment, it is a line segment. Line is the curve of the constant zero first curvature.
Circle is the curve of the constant non-zero first curvature.
Radius of the first curvature in the given regular point P(a) is a number
![]() , for 1k
, for 1k
![]() 0.
0.
For 1k=0 we speak about the infinitely large radius of the first curvature.
In the osculating plane w in the point P(a) on the curve k , there is located the osculating circle h to the circle in the given point. The centre 1S (centre of the first curvature) is the point on the normal to the curve in the given point located on the halfline determined by the point P(a) and the direction vector n(a),
in the distance of the radius of the first curvature from the point P(a), ç 1SP(a)ç = 1r,
while its radius is the radius of the first curvature 1r.
Osculating circle osculates (substitutes) the curve segment in the neighbourhood of the point P(a) (Fig. 3.3).
The elevation of the curve from its osculating plane in the given non-inflection point P(a) is represented by the second curvature - torsion 2k.
It is a real number expressed by the formula
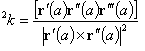
In the point of inflection on the curve, there is 2k=0.
If 2k=0 in all points on the curve, the whole curve is located in one osculating plane, it is a plane curve.
Line is the curve with the constant zero flection and torsion.
Circle is the curve with the constant first (non-zero) and second (zero) curvatures.
Helix is the curve with the constant non-zero curvatures.
Rectification of the curve segment is the development of the curve segment in the neighbourhood of the given point P(a) to the rectification plane in this point. Construction, by which the length of the curve segment can be obtained, is also called the rectification. The length of the curve segment can be also calculated from the formula
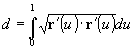
The degree of the plane curve is the number of all possible intersection points of the given plane curve and a line. Line is the curve of the degree 1, conic sections are curves of the degree 2 - quadratic curves. A curve segment interecting a line in three points is of the degree 3 - cubic, and so on.
2. Curve Modelling
Curves in the Creative space can be modelled with respect to the creative - synthetic representations, which appear in the three basic forms.
1. (a real point, a class of geometric transformations)
A point is analytically represented by a quadruple of its homogeneous coordinates A=(xA, yA, zA, 1).
2. (a curve segment, a geometric transformation)
From the given curve segment a new one can be created, applying a geometric transformation.
3. (an ordered sequence of points, an approximation or an interpolation)