Envelope Surfaces

 

Envelope of a 1-parametric system of surfaces S = { ij} is called the envelope surface F,
if it satisfies the following properties:

a) envelope F and any surface ij from the system are tangent in a curve - characteristics ik,

b) in any point on the envelope F there exists common tangent plane and
normal to the surface F and one surface ij from the system,

c) there does not exist a surface, which was simultaneously the part of envelope F and
any surface ij from the system.

System of surfaces S ={ ij } can be created from a basic surface j,
which was subdued to a class of geometric transformations (Fig. 4.115).



Envelope surface is the envelope of the images of the basic surface j by the given class of geometric transformations.

Synthetic representation: ( j, T(w) )

Analytic representations:

basic figure - p(u, v) = (x(u, v), y(u, v), z(u, v), 1), (u, v)Î<0,1>2

generating principle - class of geometric transformations T(w), wÎ<0,1>

modelled figure - s(u, v, w) = p(u, v).T(w), ( u, v, w)Î<0,1>3

Vector function s(u, v, w) in three variables represents a tri-parametric figure in the space - a solid,
envelope consists of the points on the solid boundary, which satisfy the below stated condition (I).

Characteristics k, tangent curve of the surface j and envelope F,
can be found using the common tangent plane t
in the arbitrary envelope point L.
Plane t is determined by tangent lines with the direction vectors pu, pv,
which are tangent vectors to the parametric curves on the basic surface j.

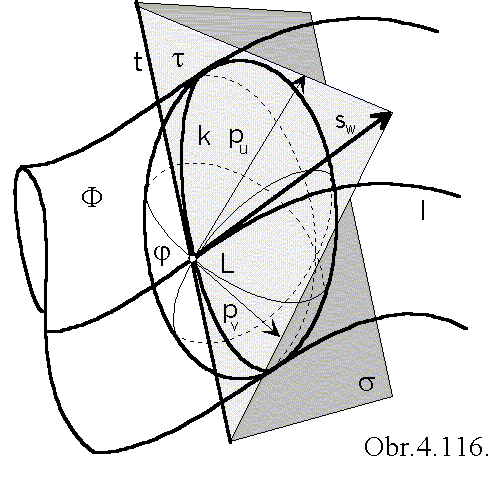
Tangent line to the curve l located on the solid boundary - envelope,
which is the trajectory of the point L,
is also located in the tangent plane t,
its direction vector sw is complanar to vectors pu, pv.
Mixed triple scalar product of three tangent vectors
to parametric curves located on the solid boundary is zero.

[pu pv, sw] = 0 ....................... (I)

Characteristics is a curve, formed by all points on the surface j, in which the above given condition (I) is satisfied.
In the case of elementary basic surfaces, characteristics is an intersection of the basic surface j by the plane s,
passing through the point L perpendicularly to the direction vector sw of the tangent line to the movement trajectory.
Intersesection line of planes s and t is the tangent line to the characteristics in the point L (Fig. 4. 116).
Envelope surface can be created also from the characteristics,
if it is subdued to the same class of geometric transformations as the basic surface j.
Envelope surface is determined by the k ( or the basic surface j) and the class of geometric transformations.

(j, T(w) » (k,T(w))

With respect to the type of the generating principle we can recognise special envelope surfaces:

homothetical (Fig. 4.117), helical(Fig. 4.118), surfaces of revolution (Fig. 4.119), translation (Fig. 4.120).

Basic surface is in the majority of practical problems a developable surface (a part of the plane) or a surface of revolution (sphere, in the Fig. 4.117 - 4.120).


                               Obr. 4.117                                                     Obr.4.118


                          Obr. 4.119                                                           Obr. 4.120

 


1. Envelope translation surfaces

Basic surface j is subdued to the class of translations determined by the vector a=(k, l, m, 0).

In the Fig. 4.121, the related views of the envelope of the system of conical surfaces of revolution
under the Monge method is given, and the axonometric view of the envelope of the system of cylindrical
surfaces of revolution, while the class of translations is determined by the vector a.


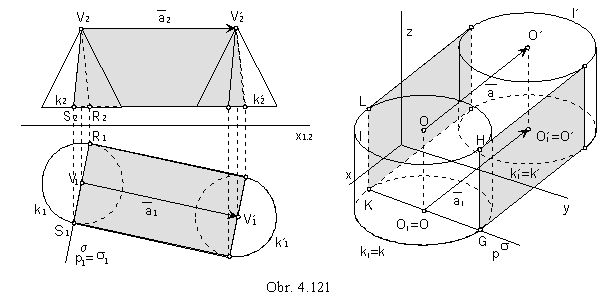
Characteristics is a polygon SVR on conical surface, a pair of line segments KL // GH on cylindrical surface,
which are planar intersections of basic surfaces by planes s perpendicular to the direction a.

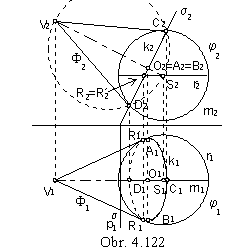
2. Envelope homothetical surfaces

Basic surface j is subdued to the class of scalings with the centre V and coefficient h0.
Characteristics k is the intersection curve of the basic surface j and the plane s perpendicular to the line,
which is the trajectory of the movement of the basic surface j.
If the basic surface is a sphere, characteristics is the tangent curve (circle) of the basic sphere j
and envelope surface F - conical surface of revolution.

 Let S be the centre of the basic sphere j with the given radius (Fig. 4.122).
Outlines of the envelope F in the front view
are tangent lines to the principle meridian m2 in the points C2, D2
passing through the point V2.
Front view of the characteristics k is the line segment C2D2
perpendicular to the front view of the line SV (axis of the envelope F).
Centre of the characteristics k is located on the envelope axis.
Ground view of the characteristics is an ellipse
with the centre O1 and minor vertices C1, D1,
while the major axis (parallel to ps) contains the major vertices A1, B1
in the distance a - equal to the radius of the circle k - from the centre O,
a=|C2O2|=|O2D2|.
 Visibility of the ground view can be determined by tangent points R and R´ of outlines of the ground view
(common points of curves r and k in the front view).

3. Envelope surfaces of revolution

Basic surface j is subdued to
the class of revolutions about the axis o.
Direction vector of the tangent line to the trajectory of the movement is perpendicular to the axis of revolution
(cicles as the movement trajectories are located in the planes perpendicular to the axis of revolution).
Plane s of the characteristics k
is passing through the axis of revolution o
perpendicularly to the tangent vector.

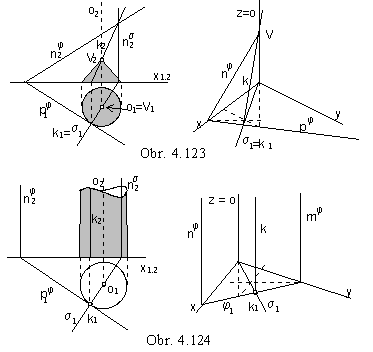
Revolving the plane j a conical surface of revolution can be created as an envelope (Fig. 4.123),
or a cylindrical surface of revolution (Fig. 4.124).
Characteristics k is the intersection line of the plane j
and the plane s, passing through the axis of revolution
perpendicularly to the plane j.
Intersection point of the characteristics and the axis of revolution is the vertex of the envelope surface
(a real point for conical, and ideal point for cylindrical surface).

 

Let the basic figure of the envelope surface of revolution be the circular cylindrical surface V with the axis o´ parallel to the frontal image plane (Fig. 4.125). On an arbitrary line m located on the surface V the point M of the characteristics k will be constructed.
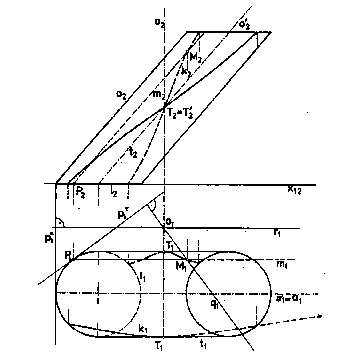Line m can be substituted by the tangent plane t
to the basic surface V in this line
and the characteristics q of the plane t,
will be determined and subdued
to the revolution about the axis o (as in the Fig. 4.123).
Line m on the basic surface intersects
characteristics q located in the tangent plane t
in the point M of the characteristics on the cylindrical surface V,
which is the Nikomedes konchoid
with the asymptote in the line o´.
Start and end points of the characteristics´ k curve segments, located on the boundary circles l and l´
of the cylindrical surface patch, can be determined in the planes,
passing through the axis of the class of revolutions o
and centres of the circles l, l´.
Points T and T´,
in which the visibility of the characteristics changes,
are located on the basic surface outlines,
the views of which coincide with the views of the tangent planes
perpendicular to the ground projection plane p.

                                                                                                                                        Fig. 4.125

In the Fig. 4.126 the sphere is the basic surfaces of the envelope surface of revolution.
Plane s, perpendicular to the tangent line t to the circle l ( trajectory of the movement ) in the point S ( centre of the sphere ),
is passing through the centre of the sphere and the axis of the class of revolutions a intersects the sphere in the circle k, which is the characteristics.


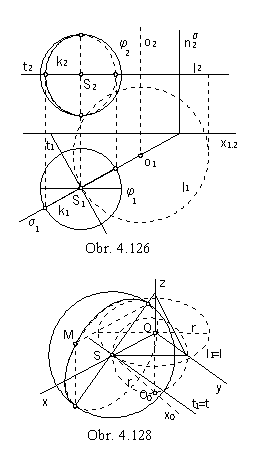
                                 Fig. 4.127

If the basic surface is the envelope surface of revolution j with the axis o´,
the points on characteristics can be found on an arbitrary parallel circle k ( centre O Îo´) on the surface j.
In the curve k, there exists a tangent sphere with the centre S on the axis o´ to the surface j ( Fig. 4. 127).
Characteristics on the sphere G ( in the same revolution movement about the axis o) is circle h,
located in the plane s passing through the centre S and axis o.
Intersection points M, M´ on circles k and h are points on the characteristics l.
It is not necessary to find the front view of the circle h, which appears in the ground view as line segment.
In the Fig. 4. 127 the principle meridian m of the created envelope surface is illustrated.

In the orthogonal axonometry, the basic sphere j with the centre S on the coordinate axis x is visualised (Fig. 4. 128).
Class of revolutions is determined by the axis in the coordinate axis z.
Revolving the ground plane to the axonometric image plane the radius of the circle l
( trajectory of the centre S movement ), r=|SO|=|SO0| can be determined.
Axonometric view of the circle l is an ellipse.
The major axis is the line parallel to the coordinate axis z, the semimajor axis equals to the radius r of the circle l.
Using the point S in the Trammel method, the size of the semiminor axis
projected in the axonometric view to the line segment on the axis z) can be determined.
Plane s passing through the axis o perpendicularly to the tangent line t to the circle l in the point S (t // y)
is the frontal image plane.
Intersection of the sphere j and frontal image plane is the principal circle k - characteristics.
Its axonometric view is an ellipse with the major axis in the side of the axonometric triangle
and semimajor axis equal to the radius r.
Point M on the ellipse can be determined on parallel lines to the views of the coordinate axes x and z.
Trammel method can be applied to find the size of the semiminor axis.
The created envelope surfaces is torus, charecteristics - circle k is the basic curve - meridian.

4. Envelope helical surfaces

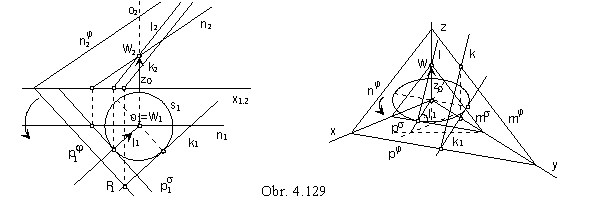
Surface j is subdued to the helical movement determined by the axis, orientation and reduced pitch z0.
In the Fig. 4.129 the plane j, intersecting the axis of helical movement o perpendicular to the ground image plane,
is the basic surface.
Charecteristics k is the line on the envelope helical surface, which is the plane of tangents to the cuspidal helix s.
Plane j is the cuspidal helix s osculating plane,
constructed characteristics k is the tangent line to the helix, located in the plane j.
Conical surface K of tangents to the cuspidal helix ( vertex WÎo, |Wp|=z0)
contains the line l parallel to the characteristics k,
tangent plane s to the surface K in the line l is parallel to the osculating plane j of the cuspidal helix s
(s can be determined by the principal line n and the plane traces can be attached).

By the helical movement of the sphere, the system of surfaces S with the envelope in the Archimedean serpentine
can be created (Fig. 4. 110).

Centre of the sphere moves on the helix s,
conical surface K of tangents to this helix has the vertex W Îo
and the basic circle h located in the plane pS
passing through the point S
and parallel to the ground image plane (Fig. 4. 130).
Tangent line t to the helix s ( trajectory of the point S)
can be constructed as parallel to the line lK.
Centre S is the point in the plane s perpendicular to the line t,
which intersects the sphere in the principal circle - characteristics k.
Plane s can be determined by principal lines
perpendicular to the line t, s=pn .
Intersection points of lines p and n with the sphere are points
A, BÎp (mapped to the major vertices of the ground view of k),
A´, B´În (major vertices of the front view of k).
The Trammel method can be used to find size of the minor axis for both views of the characteristics k.

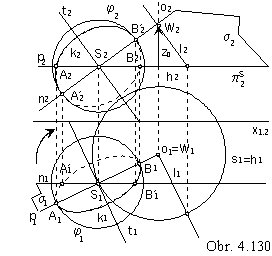
Principle meridian intersection of the Archimedean serpentine is in the Fig. 4. 131.
Intersection curve m=mÇF is the envelope of the system of circles,
which are intersections of the spheres from the system S with the plane m.
Circles, which are intersections of the basic sphere j by meridian planes,
can be found and moved in the helical movement to the intersection plane, which is the principal meridian plane m.
Centres L*, H* of circles l*, h* moved to the centres L, H in the plane m are determined.
If the angles of revolution w and w´ satisfy the equation

wS - w´ = w - wS

then the corresponding translation distances zL and zH in the given helical movement with the pitch zv satisfy equation

zS - zH = zL - zS

Points L* and H* (and circles l* and h*) are symmetric with respect to the axis of the intersection curve
passing through the point S* (moved centre of the basic sphere) perpendicularly to the axis of the helical movement o.


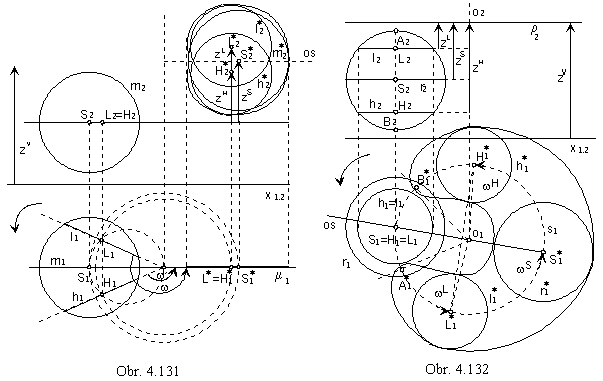
Normal intersection of the Archimedean serpentine (by the plane r perpendicular to the axis o of the helical movement)
can be found similarly to the meridian intersection. Intersections of the basic sphere by normal planes parallel to the plane r
can be moved in the helical movement to the plane r.
All centres of the intersection circles move on helices projected to one circle in the ground view.
If the translation distances zL and zH of points L, H satisfy the following equation

zH - zS = zS - zL

the corresponding angles of revolution satisfy the equation

wS - wL = wH - wS

Points L* and H* and circles l* and h* are symmetric with respect to the axis of the intersection line,
which is the envelope of all circles moved to the intersection plane,
passing through the point S* perpendicularly to the axis of the helical movement.
Angles of revolution and their corresponding translation distances in the given helical movement can be determined
by means of the Archimedean spiral.

In the construction of the characteristics on the envelope surface,
which can be created by the helical movement of the line surface (surface of revolution),
generating line (parallel circle) on the basic surface can be substituted by
the tangent plane to the basic surface in this line
(inscribed sphere tangent to the surface in this circle).
Tangent plane (sphere) can be subdued to the helical movement and the characteristics on it can be determined.
Common points on the chosen generating line (parallel circle) and this characteristics
are points on the characteristics of the created envelope surface.
In the Fig. 4. 133 the characteristics is determined in this way, the basic surface of the created envelope surface is,
: a) cylindrical surface, b) general surface of revolution.

 

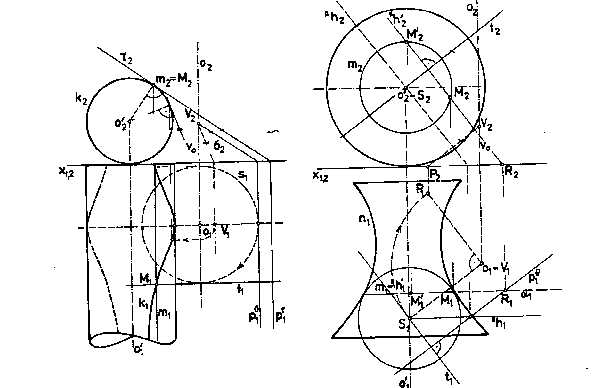
Obr. 4.133