Ts(v)=
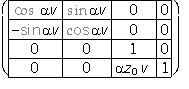 , vÎ<0,1>
, vÎ<0,1>
Helical Surfaces

Helical surface can be created by a helical movement of a curve.
Synthetic representation: ( k,TS(v) )
Analytic representations:
basic figure - r(u)=(x(u), y(u), z(u),1), uÎ<0,1>
generating principle - helical movement with the axis in the coordinate axis z
determined by translation vector a =( 0, 0, az0, 1 )
corresponding to the revolution angle 1 radian
Ts(v)=
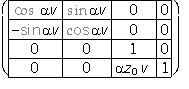 , vÎ<0,1>
, vÎ<0,1>
modelled figure -
p(u, v) = r(u).Ts(v) = (x(u)cos av-y(u)sin av, x(u)sin av-y(u)cos av, z(u)+az0v, 1),
(u, v)Î<0,1>2
k![]() 0, z0
0, z0 0 is the reduced pitch,
one pitch of the helical surface can be created for a=2p
0 is the reduced pitch,
one pitch of the helical surface can be created for a=2p
Parametric u-curves on the surface are equal to the basic curve, parametric v-curves are helices.
Neck and equator helices have the extremal radii.
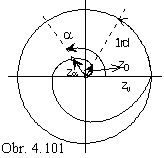
r = z0 j
v, one pitch of the spiral can be created for a=2p. Axis of the helical movement is usually located, in the Monge method,
to the line parallel to the coordinate axis z.
Movement can be determined by the pitch zv=2pz0 and by orientation.
Helical surfaces can be distributed with respect to the basic figure to:
line (line or its part is subdued to the helical movement),
cyclical (cicle or its part is subdued to the helical movement),
general (an arbitrary curve or its part is subdued to the helical movement).
Line helical surfaces are:
opened orthogonal …..opened klinogonal7nbsp; ….. closed orthogonal ….. closed klinogonal

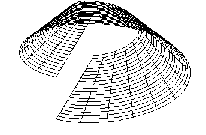

If two points on the basic line move on one helix, we speak about surface of bisecants:
opened klinogonal …..closed klinogonal


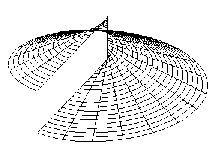
The only one developable helical surface is the surface of tangents to the helix.
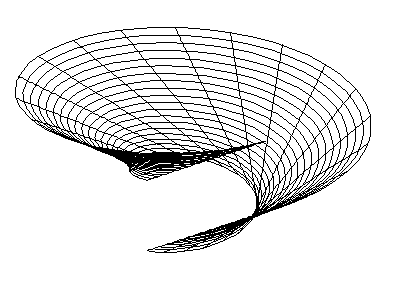
Cyclical helical surface are:
Vinded column - basic circle is located in the plane perpendicular to the axis of the helical movement
Arch surface - basic circle is located in the plane passing through the axis of the helical movement
Archimedean serpentine - basic circle is located in the plane perpendicular to the tangent line to the trajectory of the helical movement - helix of the circle centre


Tangent plane in the point on the helical surface is determined by
tangent lines to two curves located on the surface in the tangent point,
trajectory of the movement - helix, and
basic curve in the position moved to the tangent point.

Tangent plane to the line helical surface is tangent to the surfacein the basic line.
Moved position of the line to the tangent point T is one line in the tangent plane,
the other one is the tangent line to the trajectory - helix of the tangent point T.
In the construction of planar intersections of helical surfaces we usually use only two types of intersection planes:
a) normal intersection by plane perpendicular to the surface axis - normal plane,
b) meridian intersection by plane passing through the surface axis - meridian plane.
Intersection curves are constructed as sets of separate points,
which are intersections of surface helices with the intersection plane.
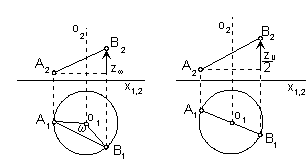
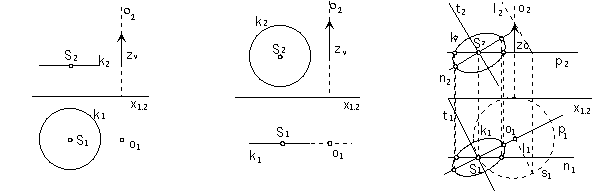
Meridian intersection of the anticlockwise helical surface determined by
the basic curve k and the pitch zv with the plane m is in the Fig. 4.112.
Points on the basic curve move in the helical movement about the axis o on helices sA, sB, sC, ... .
Movement is composed from
the revolution about the axis o to the plane m by angles aA, aB, aC, ... (in planes pA, pB, pC)
and translation by vectors a, b, c=(0, 0, zC, 0) in the direction of the axis o.
Coordiantes zA, zB, zC of the translation vectors (length of the translation vectors)
related to the revolution angles aA, aB, aC can be find using the Archimedean spiral.
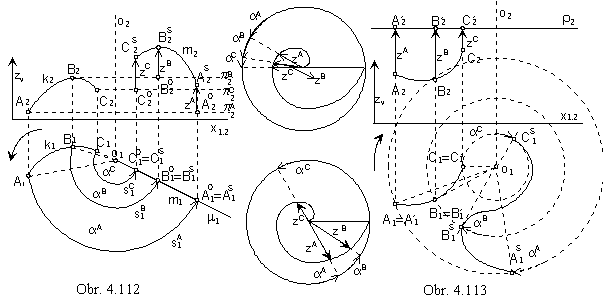
Normal intersection of the clockwise helical surface determined by
the basic curve k and pitch zv with the plane r is in the Fig. 4.113.
Helical movement can be decomposed to
translation in the direction of the vectors a, b, c
and revolution in the normal plane r perpendicular to the surface axis.
Length of translation zA, zB, zC, ...
corresponds to the angle of revolution aA, aB, aC, ... by means of the Archimedean spiral.