Creative space K

An ordered pair (U,G),

where U is the set of figures - non-empty subsets of the extended Euclidean space

and G is the set of generating principles applicable to the elements of the set U,

is denoted as Creative space K.

Geometric figures in the set U are connected subsets of the space :

 0 - dimensional (0-parametric) figure - a point, which is analytically represented by a quadruple of homogeneous coordinates, A=(xa, ya, za, 1) - a real point, or P=(xp, yp, zp, 0) - an ideal point (vector)

1 - dimensional (1-parametric) figure - a curve, or a curve segment, which is analytically represented by
a point function of one real variable

r(u)=(x(u), y(u), z(u), h(u)),  for u Î<0, 1>= W R

(a line segment, an opened or closed polygon, a curve segment, a halfline, a line, a conic section, a helix,
an interpolation curve, and others)

2 - dimensional (2-parametric) figure - a surface, or a surface patch, which is analytically represented by
a point function of two real variables

r(u, v)=(x(u, v), y(u, v), z(u, v), h(u, v)), for (u, v)Î<0, 1> x <0, 1>=W² R²

(any planar figure, for example a triangle, a polygon, a disc, a conic section including all interior points,
any polyhedron, elementary surfaces and their patches - sphere, cylindrical, prismatic, pyramidal, conical,
a torus, quadratic surfaces, helical surfaces, interpolation patches, and others)

3 - dimensional (3-parametric) figure - solid, or a solid cell, which is analytically represented by
a point function of three real variables

r(u, v, w)=(x(u, v, w), y(u, v, w), z(u, v, w), h(u, v, w)), for (u, v, w)Î<0, 1>x<0, 1>x<0, 1>=W³ R³

(elementary solids, for example a cube, a prism, a cone, a cylinder, a pyramid, a semisphere or a sphere,
a paraboloid including all interior points, a hyperboloid of two sheets including all interior points, and others)

4 - parametric figure - an animation, or an animation sequence, which is analytically represented by
a point function of four real variables

r(u, v, w, t)=(x(u, v, w, t), y(u, v, w, t), z(u, v, w, t), h(u, v, w, t)),

for (u, v, w, t)Î<0, 1>x<0, 1>x <0, 1>x<0, 1>= W⁴ R⁴

(movement of a figure in the space and time, or a solid, while its points are determined by an additional attribute
in addition to its location in the space defined by homogeneous coordinates, by a temperature, or so).

Disconected (discrete) subsets are ordered sets:

           1D sequences                                       2D nets                                     3D grids of points

      sequences                                         nets                                 grids of curve segments

                sequences                                             grids of surface patches

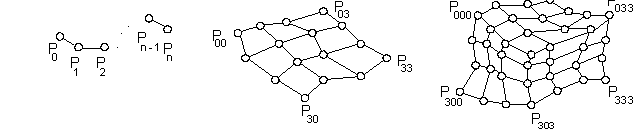
ordered sequences of solid cells, and others.

Discrete ordered sets of geometric figures are analytically represented by maps - martices M, which elements are analytic representations of separate geometric figures in the given order.
New figures, elements of the set U, will be created from the given figures, using generating principles.

Generating principles from the set G are:

Geometric transformations

Applying a geometric transformation to the figure we can create a figure of the same dimension as was that of the original one, it means, a point can be mapped to a point only, a curve to a curve, and so on.
With respect to the type of the geometric transformation,
- there can be invariant size of the figure and only the position of the figure in the space can be changed (Euclidean transformations),
- or both the shape and position of the figure can be changed (affine, or projective transformations).
For instance, from a circle there can be created an ellipse applying axial affinity,
or any conic section (ellipse, parabola, or hyperbola) applying a central collineation.
Similarly, we can create any quadratic surface from a sphere, an ellipsoid - applying an affine transformation,
an ellipsoid, a paraboloid, a hyperboloid - applying a projective transformation.
Geometric transformations are analytically represented by regular square matrices of rank 4 with real elements.

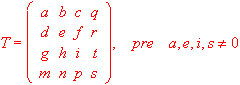
Elements of the matrix represent coefficients of geometric transformations.

q, r, t are coefficients of projective transformations, for affinne transformations q=t=r=0

(m, n, p) are Cartesian coordinates of the translation vector

a, e, i 0 are coefficients of scalings on coordinate axes x, y, z

s 0 is the inverse value of the coefficient of homothety to the centre in the origin.

Classes of Geometric Transformations

An infinite set of geometric transformations of the same type is denoted as a class.
Applying a class of geometric transformations to the geometric figure a new geometric figure,
of the dimension greater by 1 then the one of the former figure, can be created.
For example, from the point A (0-dimensional figure) there can be created
by the class of revolutions about the axis o by angles from the interval <0,2p>
the circle (1-dimensional figure, Fig. 1.25),
while revolving the line segment AS^A (1-dimensional figure)
the whole disc (2-dimensional figure) can be created.

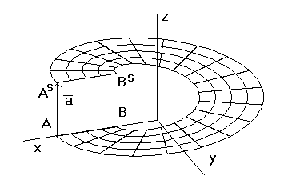Fig. 1.26

By a helical movement of the line segment AB about the axis z
determined by angles of revolution from the interval <0,2p>
related to translation vectors in direction of the axis from the interval <0,a>, a=(0, 0, y, 0)
we can create the helical surface patch with the boundary curve segments in
- line segments AB, A^SB^S and helical arcs AA^S , BB^S (Fig. 1.26).
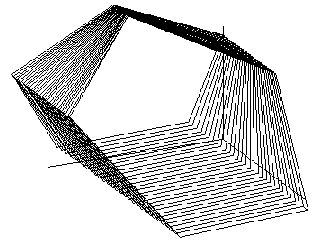
Similarly, we can create from the curve - circle k, for instance a conical surface patch, taking for the generating principle a class of hometheties to the centre in the arbitrary real point V in the space and coefficients from the interval <0,1> (Fig. 1.27). Applying separate homotheties from the given class for values from the given interval we obtain a continuous set of circles with minimising radii located more and more closely to the centre V with the point V at the end, which create a conical surface patch inbetween the vertex V and the basic circle k. Truncated prismatic surface patch can be created from the basic polygon, while the applying generating principle is the class of axial affinities (Fig. 1.28).

                                            Obr. 1.27                                                        Obr. 1.28

Classes of geometric transformations are analytically represented by
regular square matrices of rank 4 - functions T(u), which elements are real functions of one variable,
all defined, continuous and at least once differentiable on the interval I.
For the unificated denotation in the computer processing we will require I=<0,1>.

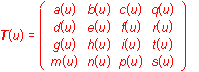, is the matrix of the system of equations

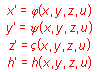
In the case of the class of affine transformations, q(u)=r(u)=t(u)=0 for any uÎ<0,1>,
for classes of metric transformations, IT(u)I² =1 for any uÎ<0,1>.

Approximation (interpolation)

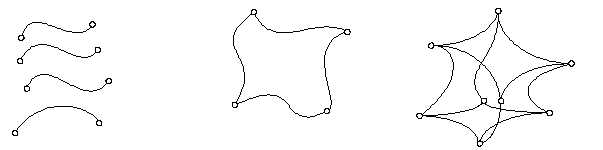
There can be created, from the discrete subsets of the space by methods used in the computer graphics, geometric figures, which are denoted with respect to the applied generating principle as interpolation, or approximation figures. Approximation is the generating principle by means of which we can create from discrete figures the connected ones - geometric figures. Simplifying, we fill the space inbetween the given discrete figures according to the preset criteria,
which can be, for example, in the form of the required geometric and physical properties of the created figure.

If the modelled figure must contain all elements of the former discrete set - basic figure, we speak about the interpolation.

If this condition need not be fulfilled and the basic figure is only a certain boundary determining the space, in which the modelled figure must be located, we speak about the approximation.

Analytic representation of an approximation (interpolation) is a matrix I(u) of type 1xn, with elements in polynomial functions of degree n-1 satisfying certain criteria.

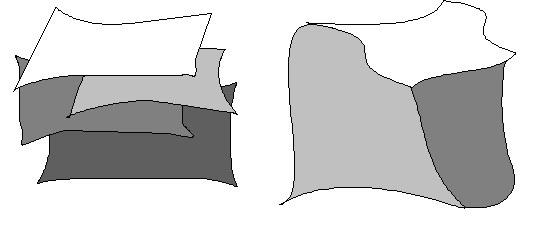
Modelled figure is determined uniquely by its creative law, synthetic construction, under which it is created from the basic figure U applying the suitable generating principle g.

Creative - synthetic representation of the modelled figure V
is any ordered pair (U, g), where
UÎU is the basic figure
and gÎG is the generating principle such,
that applying the generating principle g to the basic figure U
the modelled figure V can be created.

Analytic representation of the modelled figure can be abtained as the multiplication of the analytic representations of the basic figure and the generating principle from the creative - synthetic representation.

Modelled figures in the space can be projected to the image plane (drawing paper, computer screen, or a plotter) and visualised under one from the numerous projection methods, by hand or using any output graphical device.

Scene is a triple (MU, PM, AV),with elements:

MU - set of modelled figures

PM - projection method for visualisation of figures

AV - algorithm of visibility, by means of which we can delete those parts of the figure, which are invisible on the concerned view of the figure, or all other algorithms of the computer graphics, providing realistic visualisation of the scene, e.g. filling, shading, enlightening, colour, brightness, and so on.