Homothetic surfaces
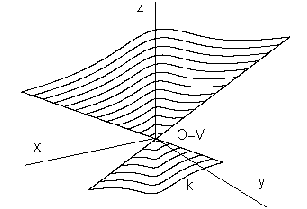 Homothetic surface can be created
from the basic curve segment k by applying a class of homotheties to the given centre V
with the scaling coefficient h
Homothetic surface can be created
from the basic curve segment k by applying a class of homotheties to the given centre V
with the scaling coefficient h  0.
0.
Point V is the vertex of the homothetic surface (obr. 4.38).
Choosing the value of the coefficient h ¹ 0
the form and size of the modelled patch is determined.
From the basic polygon k a pyramidal surface patch can be created with the main vertex not located on any of the polygon sides (obr. 4.39),
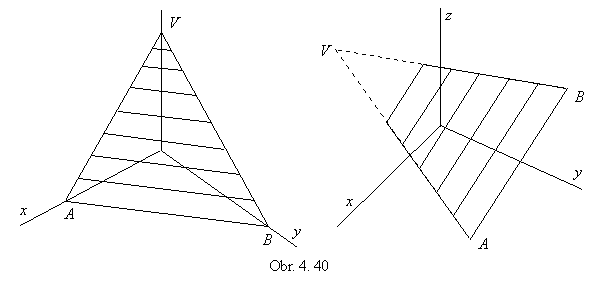
if k is a line segment, triangle is determined for h = 1,
or a trapezoid for h < 1) (obr. 4.40).
Conical surface patch can be modelled from an arbitrary curve segment.
If the basic curve is a planar one, centre V of the class of homotheties must not be located in the same plane.
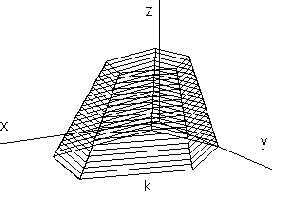
Obr. 4. 39
Conical surface
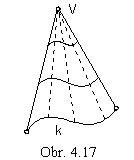 From the curve segment k
a conical surface can be created applying a class of homotheties with the centre V and a nonzero
scaling coefficient h (obr. 4.17).
From the curve segment k
a conical surface can be created applying a class of homotheties with the centre V and a nonzero
scaling coefficient h (obr. 4.17).
Synthetic representation: (k, TR(v))
Analytic representation:
basic figure - curve segment k
r(u) = (x(u), y(u), z(u), 1), u Î < 0, 1 >
generating principle - class of homotheties with the centre V =
(xv, yv, zv, 1) and coefficient
h  0,
0,
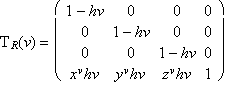 , v Î < 0, 1 >
, v Î < 0, 1 >
modelled figure
p(u, v) = r(u) . TR(v) =
((1-hv) x(u) + xvhv,
(1-hv) y(u) + yvhv,
(1-hv) z(u) + zvhv, 1), (u, v)Î< 0, 1 >2

h > 1 conical surface of two sheets
h = 1 simple conical surface with the vertex V
0 < h < 1 frustum of the conical surface in the half-space determined by the basic curve segment k and vertex V
h < 0 frustum of the conical surface in the opposite half-space to the one determined by the basic curve segment k and vertex V
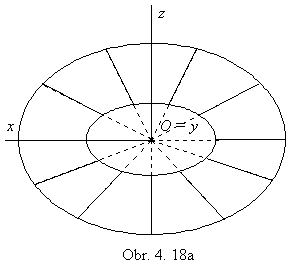
If k is a planar curve segment, k  a
and centre V is located in the plane a, a conical surface patch, which is a part of the plane
a is created (obr. 4.18a, coefficient h < 1).
a
and centre V is located in the plane a, a conical surface patch, which is a part of the plane
a is created (obr. 4.18a, coefficient h < 1).
If k is a circle in the plane a and centre V is not located in the plane
a, a circular conical surface with the vertex V is created.
In case, a line passing through the vertex V perpendicularly to the plane a of the basic circle
intersects this plane in the circle k centre, the created surface is a patch of the conical surface of revolution.
Obr. 4. 19
Obr. 4. 20
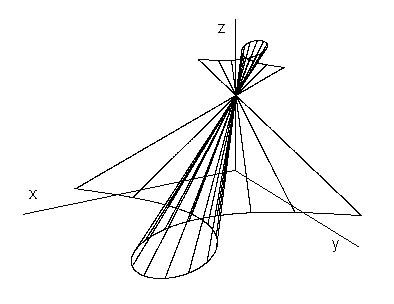
Illustration of the conical surface patch with the basic curve in the Folium of Descartes is in the Obr. 4.19, coefficient h > 1.
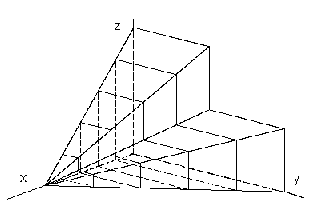
If k is a polygon and vertex V is not a point n this curve, modelled surface is a part of the pyramidal surface
with vertex V created from planar patches (obr. 4.20, coefficient h = 1).
 Homothetic surface can be created
from the basic curve segment k by applying a class of homotheties to the given centre V
with the scaling coefficient h
Homothetic surface can be created
from the basic curve segment k by applying a class of homotheties to the given centre V
with the scaling coefficient h 

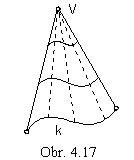 From the curve segment k
a conical surface can be created applying a class of homotheties with the centre V and a nonzero
scaling coefficient h (obr. 4.17).
From the curve segment k
a conical surface can be created applying a class of homotheties with the centre V and a nonzero
scaling coefficient h (obr. 4.17). 0,
0,
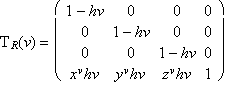 , v Î < 0, 1 >
, v Î < 0, 1 >


