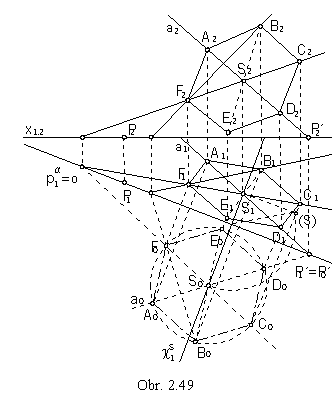
 Problem 1.: Find related views of a regular
hexagon in the plane
Problem 1.: Find related views of a regular
hexagon in the plane Views of planar figures
In the construction of views of planar figures determined
by their metric properties and in the reconstruction of the true form and size of planar figures determined by their related orthographic views,
the construction of the revolution of the figure plane to the image plane, or to the plane parallel to the image plane is used.
Views of points in the plane a and views of revolved points in the revolved position of the plane
a0 form pairs of points in the image plane related in the axial affinity.
Axis of affinity is the view of the axis of revolution (set of all invariant points), which is the intersection line of the revolved plane
a and the plane, to which the revolution is performed (the image plane, or the plane parallel to the image plane),
therefore this is a trace, or a principal line of the plane a.
Direction of affinity is perpendicular to the axis of affinity, axis of revolution.
Point and its revolved position are located in one plane of revolution perpendicular to the axis of revolution,
which appears in the related image plane as a line perpendicular to the view of the axis of revolution, passing through both,
the view of the point and the view of its revolved position.
Revolution of one point in the plane determines the revolution of the entire plane.
Axial affinity is determined between any plane and its revolved position, axis of affinity is in the axis of revolution,
direction of affinity is perpendicular to the axis of affinity and a pair of corresponding points form views of the point
in the plane a and its revolved position.
 Problem 1.: Find related views of a regular
hexagon in the plane
Problem 1.: Find related views of a regular
hexagon in the plane
Solution: Line PP´, where P´ is the trace of line a = AS is the trace of the plane a in the ground image plane.
We will revolve the plane a about the trace pa
to the ground image plane.
Point S will move in the plane of revolution cS perpendicular to the ground image plane
p to the point S0.
Line a = AS will be revolved to the line a0 = P´0S0,
which can be determined by the invariant point P´ = P´0 and the point S0.
Revolved point A0 is located on the revolved line a0 and it is the affine image of the point A ground view.
Direction of affinity is perpendicular to the axis of revolution, which is also the axis of affinity.
Revolved hexagon A0B0C0D0E0F0
with the centre S0 appears in the true size and shape.
Its ground view can be determined by means of the axial affinity, to vertices B0 to F0
the affine images B1 to F1can be attached.
Invariant points of lines used to determine views of the hexagon vertices in the affinity
are traces of these lines located on the trace of the plane a in the ground image plane, and they are located on the
reference line x1,2 in the front views.
Front views of the hexagon vertices can be found on the front views of the corresponding lines.
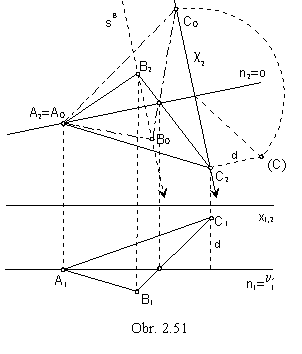
Problem 2.: Find the true size of the triangle
ABC determined by related views of its three vertices (obr. 2.51).
Solution:
Vertices of the triangle ABC determine the plane a, which must be revolved to one image plane in order to receive the true size of the triangle.
In the figure, the plane is revolved to the plane parallel to the frontal plane.
Axis of revolution is the line n = n´ Ç a,
which is the principle line of the second frame in the plane a.
Point A on the axis of revolution is an invariant point.
Point C revolves to the point C0 in the plane of revolution c
perpendicular to the axis of revolution.
Pair of points C2 and C0 is the pair of corresponding points in the axial
affinity with the axis in the line n2
and direction perpendicular to the axis determined by the view
c2
of the plane of revolution of the point C.
Affine image of the line segment
B2C2 is the revolved line segment
C0B0.
It is passing through the invariant point on the axis of affinity, while the point
B0 is located on the line sB in the direction of affinity.
Triangle A0B0C0
is congruent to the real triangle ABC.
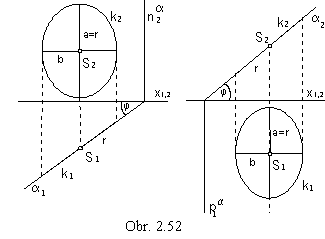
Orthographic view of a circle can appear as:
a) a line segment, if the circle is located in the plane perpendicular to the image plane,
b) a circle, if the circle is located in the plane parallel to the image plane, or in the image plane,
c) an ellipse, if the circle is located in a different plane a than mentioned above.
Major axis of the ellipse is in the view of the principal line in the plane a parallel to the image plane (size of the semi-major axis is equal to the radius of the circle a = r ) and minor axis is in the view of the slope line in the plane a perpendicular to the principle line (size of the semi-minor axis is b = r cos j, while j is the angle that the plane a forms to the image plane).
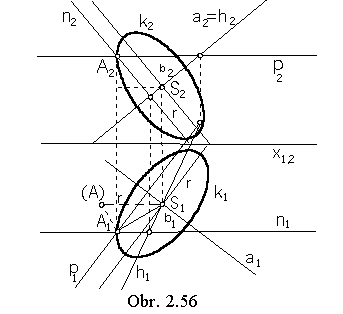
In the obr 2.52, there are related views of the circle k located in the plane
a perpendicular to the ground image plane (left) and frontal image plane (right).
In the obr 2.53 related views of the circle k located in the plane r
(axonometric image plane) determined by traces are illusteted.
Ground view of the circle is an ellipse with the major vertices in points A1,
B1 on the ground view p1 of the principal line of the first frame in the distance equal to the radius
r of the circle from the ground view of the centre S1 of the circle.
Front view of the circle is an ellipse with the major vertices in the points A´2 , B´2 on the front view
n2 of the principal line of the second frame in the distance equal to the radius r
of the circle from the front view S2 of the circle centre.
Points A2, B2,
A´1, B´1 are points on corresponding views of the circle k.
Minor axis of the ellipse in the ground view is in the view of the slope line of the first frame 1s1,
minor axis of the ellipse in the front view is in the view of the slope line of the second frame 2s2.
Semi-minor axes for the ellipses in the separate views can be found by lowering the projecting planes of the related slope lines,
scaling the size of line segments
| CS | = | SD | = | C´S | = | SD´ | = r.
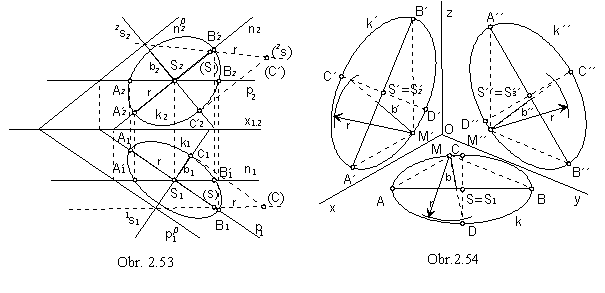
Axonometric view of the circle located in one of the the coordinate planes is an ellipse (obr. 2.54 ).
Major axis of the ellipse is line parallel to the intersection line of the axonometric image plane and the corresponding coordinate plane,
which means line parallel to one side of the axonometric triangle XY, XZ, YZ.
It is passing through the related view of the circle centre S.
Size of the semi-major axis equals to the radius r of the circle.
Semi-minor axis is parallel to the view of the coordinate axis perpendicular to the coordinate plane, in which the circle is located - z (y, or x).
One more point on the circle M ( M´, or M´´ ) can be determined as the view of the point located on the circle,
and therefore, as a vertex of a right angle in the triangle ABM (A´B´M´, or A´´B´´M´´) with the hypotenuse AB
(A´B´, or A´´B´´).
View of the right angle in the coresponding coordinate plane
p ( n, or
m) is the angle of the views of coordinate axes x and y ( x and z,
or y and z ).
Minor vertices can be determined from the following relations
| CS | = | SD | = b ( | C´S´ | = | S´D´ | = b´, or | C´S´ | = | S´D´ | = b´´ ).
Solution: