( with the ideal line
 v=
v= V
V V´).
V´).Intersections of elementary surfaces
Pyramidal, prismatic, conical and cylindrical surface are created by lines passing through the
real or ideal surface vertex.
Intersection of surfaces is the set of all intersection points on one surfaces with the other surface.
Intersection can be a total intersection (two closed figures), if all lines on one surface intersect the other surface.
In the case of a partial intersection ( one closed figure), on one of the surfaces there are lines not intersecting the other surface.
The problem to find intersection points of a line and a surface can be solved by means of vertex planes passing through the vertices of both intersecting surfaces.
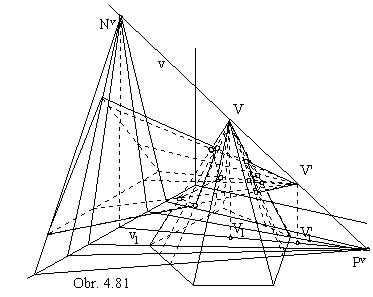
When both vertices are two different points V and V´ ,
all vertex planes will be passing through the vertex line determined as v = VV´.
In the case of intersection of pyramidal or cylindrical surfaces, the vertex line is determined by two real points,
in the case of intersection of prismatic and pyramidal (or conical and cylindrical) surfaces, the vertex line is determined by one real and one ideal point ,
and in the case of intersection of two prismatic (or cylindrical) surfaces, the vertex line is determined by two ideal points.
System of auxhiliary planes ij will form a lattice ( a pencil ) of planes with the axis in the line v = VV´
( with the ideal line  v=
v= V
V V´).
V´).
Planes intersect both surfaces in two lines, or they are tangent to the intersecting surfaces in one line, or in one face.
Tangent planes are called support planes.
A pair of support planes for each of the two surfaces F, Y form a wedge (a layer) for the related surface.
Intersection of surfaces F Ç Y = c is located in the intersection of the two related wedges (layers).
If the boundary planes of the intersection wedge (layer) are support planes for one of the surfaces,
the intersection is total, in the opposite case it is partial.
Boundary plane of the intersection wedge (layer) will separate from the surface for which it is not the support plane the part not participating in the intersection.
1. Intersections of pyramidal and prismatic surfaces
Intersection is a polygon in the space (not necessarily a planar one),
with vertices in intersection points of edges on each of the surfaces with the other surface.
Separate points of intersection polygon can be constructed as follows:
1. Vertex line v and its traces are determined in those coordinate planes, in which basic polygons of the intersection surfaces are located.
Traces of the auxhiliary vertex planes (passing through the line v) are determined by these points.
2. Boundary planes of the intersection wedge are found,
and parts not participating in the intersection are separated on both surfaces,
while the type of intersection is determined in this way.
3. Vertex planes ij are located in all edges of one surface located in the intersection wedge (participating in the intersection),
and their intersection lines with the other surface are determined.
Intersections of these lines on one surface and related edges on the other one, all located in one of the auxhiliary vertex plane are vertices of the intersection polygon.
4. Sides of the intersection polygon are determined by vertices in the correct order,
so that each side is the intersection line segment of one surface face with the other surface face.
The part of the intersection located on visible faces on both surfaces is visible.
Total intersection of two pzramidal surfaces with basic polygons in coordinate planes p and n and vertices V, V'
is mapped in the orthogonal axonometry in obr. 4.81.
To make the construction easy to survey, it is convinient to number found vertices of intersection in a suitable way, in order to receive an ordered sequence of vertices.
After all vertex planes in the step 3 are determined,
the intersection points of plane traces and basic figures of both surfaces are numbered.
We can start numbering in the vertex located on the boundary púlane of the intersection wedge (layer).
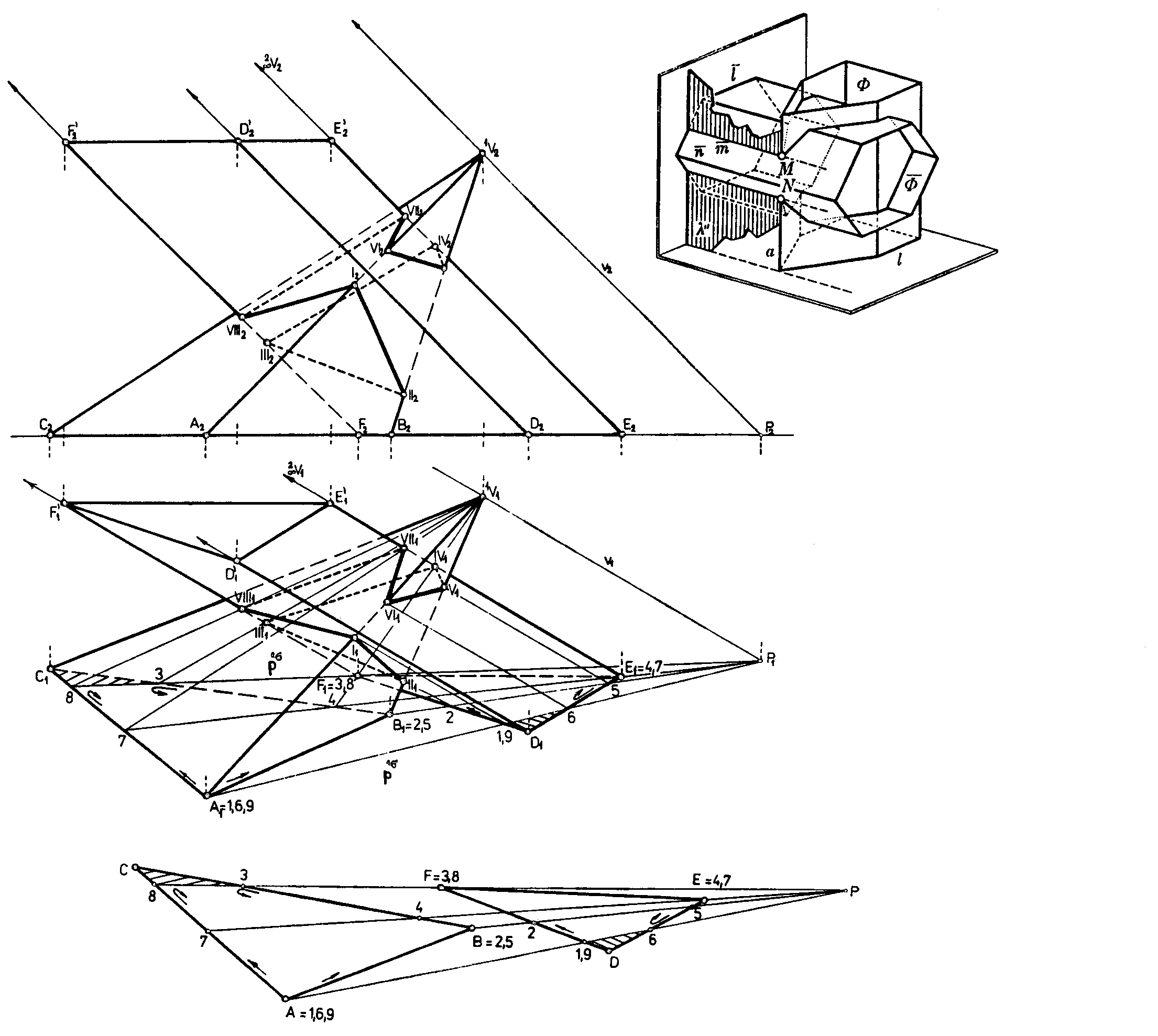
In obr. 4.82, number 1 is attached to the vertex A on the pyramidal surface,
and the same number is attached to one of the intersection points of the trace of intersection wedge (layer) boundary plane with the basic figure of the other surface,
sides of the triangle DEF.
Next closest vertex plane in the intersection wedge is passing through the vertex B of the pyramidal surface,
this is marked as number 2, the same way as one of the
intersection points of the vertex plane trace and the triangleDEF.
In this way, we have determined the orientation of movement on basic figures of intersecting surfaces.
In this direction (arrows in obr. 4.82), the next closest vertex is the vertex on the prismatic surfaceF = 3,
vertex plane passing through this vertex is boundary plane of the intersection wedge,
and its trace intersects the basic figure of the pyramidal surface
- triangle ABC in two points,
number 3 will be attached to that one, which is next to the point B = 2 in the given orientation.
Number 4 will be attached to the next closest vertex E on the prismatic surface,
and to the intersection point of the trace of vertex plane passing through the point E with the side BC of the pyramidal surface basic figure in the given orientation
(from the point 3 we are returning back to the point 4).
In the same way, next numbers are attached till we are not back in the point,
which has allready two numbers attached (in obr. 4.82 it is point 1 = 6 = 9).
Lines on different surfaces passing through the points on basic figures with the same number are located in the same vertex plane,
and therefore they intersect in the vertices of the intersection polygon, which are attached the same number.
From the sides of the intersection polygon determined by the sequence of points,
those are visible, which are located in visible faces on both surfaces.
While numbering, we will go around twice on those parts of basic figures,
on which traces of lines located on surfaces and participating in the intersection are located.
Numbering is correct, if all vertices on edges participating in the intersection are attached two numbers,
but the vertex, in which we started the numbering.
The first vertex must be attached three numbers in the case of partial intersection (obr. 4.82),
and four numbers in the case of total intersection.
In obr. 4.83, the axonometric view of the partial intersection of prismatic surfaces with basic figures in the coordinate planes p and n is illustrated.
Vertex planes form a layer of planes parallel to the coordinate plane
m,
their traces in the ground plane and in the frontal plane are parallel to the coordinate axes y and z respectively.
Intersection is a polygon.
2. Intersections of conical and cylindrical surfaces
Intersection is a closed space curve (a pair of closed curves) od degree four (both surfaces are of degree two - quadratic),
set of all intersections points of lines located on one surface with the other one.
In construction of these points we follow the algorithm described above.
The most important planes from the system of vertex planes are those passing through the oulines of both surfaces, if located in the intersction wedge.
Points of intersection curve located on these lines can be the boundary points of the visible parts of the related view of intersection curve.
Tangent line to the intersection curve in the point L is the intersection line of tangent planes to different surfaces in their common point L.
Tangent plane to the cylindrical (conical) surface in the point L is determined by the surface line p passing through the given tangent point
and tangent line to the basic circle of the surface in its common point with the line p.
Orthogonal axonometric view of the total intersection of the conical surface of revolution and cylindrical surface of revolution is illustrated in obr. 4.84.
In the point L, tangent line to the intersection curve is determined.
In obr. 4. 85, axonometric view of the total intersection of two cylindrical surfaces of revolution with basic circles in ground plane and in frontal plane is presented.
Ideal vertex line is located in the side plane, auxhiliary vertex planes are parallel to the side plane.
Boundary planes of the intersection layer are tangent planes to the cylindrical surfaces,
plane 1s is the common support plane of both surfaces,
it is tangent in lines 1p, 2p,
which intersect in the double point of intersection curve.
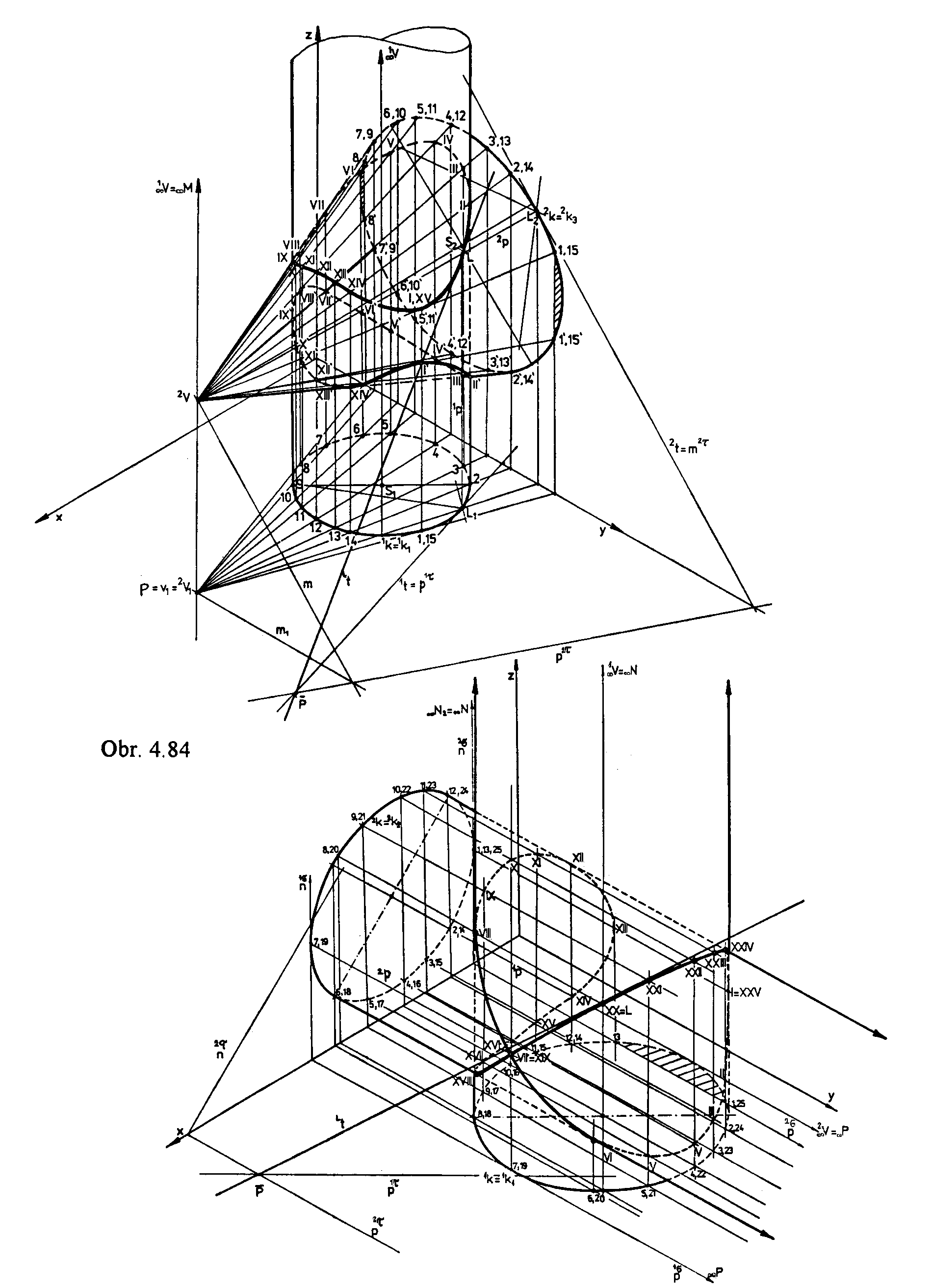
Obr. 4. 85
3. Intersections of pyramidal and prismatic surfaces with conical and cylindrical surfaces
In precise constructions of the intersection curves, there must be determined basic elements of intersection curve segments - conic sections,
in which faces of pyramidal or prismatic surfaces,
participating in the intersection, intersect respective coniucal or cylindrical surfaces.
Closed intersection curve (pair of curves) is composed from segments of conic secrtions.
In sketching, the same approach can be adopted as in the previous problems.
4. Intersections of sphere and elementary surfaces
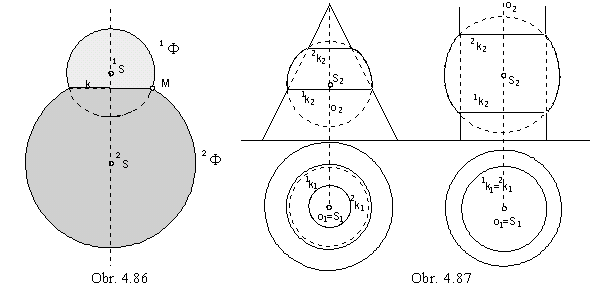
Intersection of two spheres
1F = ( 1S, 1r ), 2F = ( 2S, 2r ) is
empty set
1F Ç 2F = { }, |1S 2S| > 1r +2rone single point 1F Ç 2F = {T}, |1S 2S| = 1r + 2r
circle
1F Ç 2F = k, |1S 2S| < 1r + 2r . Circle k is located in the plane perpendicular to the line 1S 2S and its centre is on this line.
Orthographic view of k to the plane parallel to the line 1S 2S is line segment perpendicular to the view of line
1S 2S (obr. 4. 86).
One point of the intersection circle k is, for example, the common point M on outlines of spheres 1F , 2F.
Intersection of sphere and pyramidal or prismatic surface is a curve composed from circular arcs,
which are intersections of sphere by separate faces of these surfaces.
If centre of the sphere F= (S, r) is located on axis of the conical or cylindrical surface of revolution,
intersection is a pair of circles located in planes perpendicular to the axis of the surface of revolution.
These are mapped orthographically to the plane parallel to the axis as line segments (obr. 4. 87).
If centre S of the sphere F is not located on the axis of the surface of revolution,
intersection must be constructed as intersection of two surfaces of revolution.
Intersection of sphere and conical or cylindrical surface, which is not the surface of revolution, BR>
can be determined as a set of intersection points of lines on the concerned surface with the sphere by means of the system of auxhiliary planes.
Tangent line to the intersection curve can be constructed in all points.