(ideal point
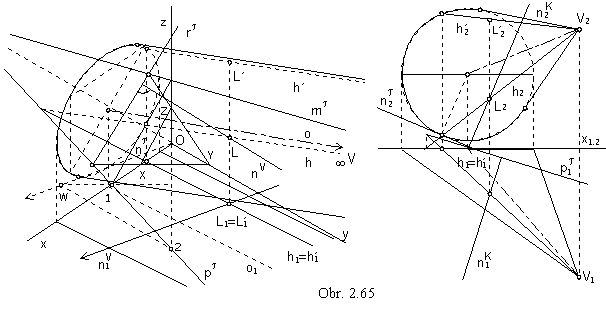
View of the surface can be determined by the view of the basic curve and by views of the contoure line segments on the surface patch
forming the view outline (obr. 2.65).
Views fo conical (cylindrical) surfaces nad cones (cylinders)
Conical (cylindrical) surface is determined by the basic curve (usually a circle) and a main vertex, which is a real point V
(ideal point ![]() V, direction of all lines on the surcface).
V, direction of all lines on the surcface).
View of the surface can be determined by the view of the basic curve and by views of the contoure line segments on the surface patch
forming the view outline (obr. 2.65).
Let the ground view of the point L on the surface be given. Line h is passing through the point L on the surface. Front views of a couple of lines h and h´ on the surface sharing the common ground views h1 = h1´ can be determined by the intersection points of these lines and basic circle of the surface, which are traces of lines. Ground views of points L and L´ are located on the ground views of lines. Axonometric views of points L and L´ can be determined on the axonometric views of lines. Tangent plane t in the point L on the conical (cylindrical) surface is formed by the line h passing through the point L on the surface and the tangent line (which is one plane trace) to the basic circle in its common point with the line h . Normal n is perpendicular to the tangent plane t.
Intersections of cylindrical surfaces
Direction plane s of the cylindrical surface V is the plane passing through the surface ideal point
![]() V.
V.
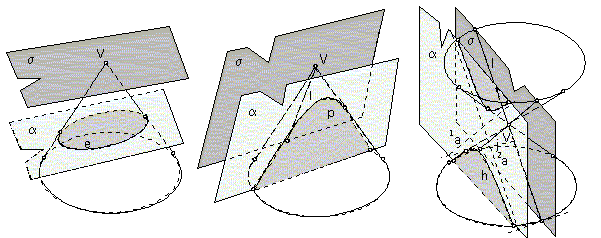
Intersection figure of the plane s and cylindrical surface V ca be:
1. one line on the surface (tangent plane),
2. a pair of lines on the surface,
3. an empty set.
Plane a, which is not the direction plane of the circular cylindrical surface,
intersects the surface in an ellipse, or a circle.
Centre of the intersection curve is located on the axis of the cylindrical surface.
Any two planar intersections on the cylindrical surface by planes a and a´,
which are not direction planes,
are related in the axial affinity with the axis in the intersection line of the two planes
a and a´.
Direction of affinity is determined by the direction of lines on the cylindrical surface
and a pair of corresponding points is in the centres of the intersection curves,
which are intersection points of the intersection plane and the surface axis (obr. 2. 72).

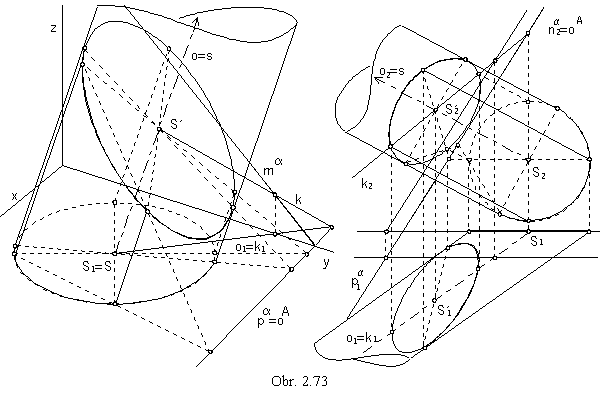
On the obr 2.73, a planar intersection of the circular cylindrical surface with the basic circle in the ground plane is presented in the orthogonal axonometry, and related views of the planar intersection of the circular cylindrical surface with the basic circle in the frontal plane are mapped in the Monge method.
Intersections of conical surfaces
Plane passing through the vertex V of the conical surface is vertex plane.
Vertex plane s can intersect conical surface in the following figures:
1. one point V,
2. one line on the surface (tangent plane),
3. two lines on the surface.
Plane a, which is not the vertex plane of the circular conical surface K,
can intersect the surface in a conic section
(or a circle, if it is parallel to the plane of the surface basic circle).
Type of the intersection conic section is determined by the form of the intersection figure by the vertex plane s parallel to the intersection plane.
Intersection curve of the conical surface by the plane a is:
a) an ellipse, if the intersection figure is a point, s Ç K = V, a Ç K = e
b) a parabola, if the intersection figure is a line, s Ç K = l, a Ç K = p
c) a hyperbola, if the intersection figure is a pair of lines, s Ç K = l, j, a Ç K = h
Any two planar intersection on the conical surface by planes a and a´,
which are not vertex plabnes, are related in the central collineation correspondence, with the axis in the intersection line of planes
a and a´, centre in the surface vertex and a pair of corresponding points
in the pair of intersection points of the intersection planes a and a´ and one of the surface lines (obr. 2.76).

Orthographic view of the ellipse located on the conical surface of revolution
into the plane perpendicular to the surface axis is an ellipse with one focus in the view of the surface vertex (obr. 2.77).
Front view of the intersection ellipse is a line segment A2B2,
with the end points mapped to the major vertices of the intersection ellipse ground view, located on the intersection plane slope line of the first frame.
Centre of the intersection ellipse is in the centre of the line segment AB.
Minor vertices C and D of the intersection ellipse ground view are located on the principal line of the first frame passing through the centre
O of the ellipse.
V1 is the focus of the intersection ellipse ground view.
The intersection ellipse is entirely visible in the ground view.
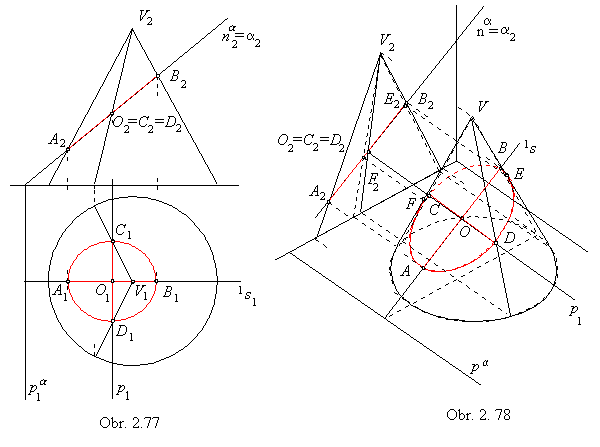
In the obr. 2.78, the elliptic intersection of the conical surface of revolution by the plane a is illustrated in the orthogonal axonometry.
Axonometric view of the intersection is determined by the conjugate diameters AB, CD.
Diameter AB is located on the slope line of the first frame 1s of the intersection plane a.
Vertex plane s = V 1s intersects conical surface in two lines intersecting line
1s in points A, B on the intersection.
Centre O of the line segment AB is the centre of the intersection.
Conjugate diameter to the diamater AB of the intersection ellipse is located on the principal line p of the first frame.
Plane s = Vp intersects conical surface in lines CV and DV,
while points C and D are located on the line p.
Visibility can be determined by the intersection points E, F of the intersection plane and outlines of the conical surface.
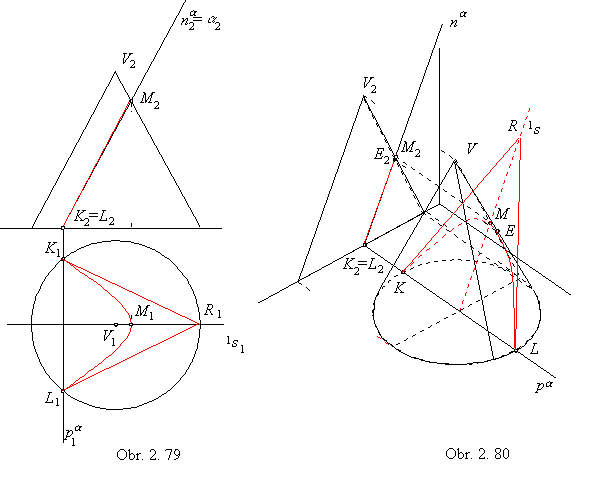
In the case of a parabolic intersection on the conical surface of revolution K, the intersection plane is parallel to one of the surface lines.
Parallel vertex plane is a tangent plane to the conical surface.
In the obr. 2.79, the parabolic intersection on the conical surface of revolution by the plane a is illustrated in the Monge method.
Vertex plane s || a is tangent to the conical surface of revolution in the ouline of the surface front view.
Trace of the vertex plane s in the ground image plane is the tangent line to the basic circle k.
Trace of the intersection plane a intersects circle k in the end points of the parabolic segment of intersection.
Front view of the intersection plane is the line a2
intersecting the outline of the conical surface front view in the point M2,
which is the extremal point of the parabolic intersection with respect to its distance from the ground image plane.
Front view of this point is located on the slope line of the first frame 1s1 in the intersection plane,
which mappes to the axis of the intersection ground view.
Vertex of the conical surface of revolution mappes in the ground view to the focus of the intersection parabola ground view.
Tangent lines to the intersection parabola in the points K, L can be attached with respect to the property of subtangent.
Axonometric view (obr. 2.80) of the parabolic intersection on the conical surface of revolution by the plane a perpendicular to the frontal plane can be determined by the slope line of the first frame 1s in the intersection plane, which is in the direction of the intersection parabola axis and intersects surface in the point M located in the maximal distance from the ground image plane.
Orthographic view of a hyperbola on a conical surface of revolution onto the plane perpendicular to the surface axis is a hyperbola with one focus in the view of the surface vertex.
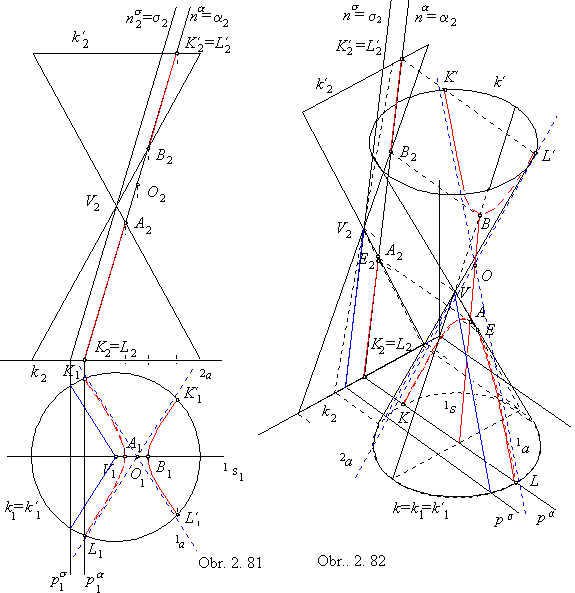
In the obr. 2.81, there is illustrated the hyperbolic intersection of the conical surface of revolution by the plane a in the Monge method.
Vertex plane s is passing through the surface vertex V parallelly
to the intersection plane a and intersects surface in a pair of lines.
These lines determine the directions of intersection hyperbola asymptotes 1a, 2a.
Slope line of the first frame 1s in the intersection plane mappes to the gound view as the axis of the intersection hyperbola ground view,
its intersection points A, B with the surface are mapped to the ground views as major vertices of the intersection hyperbola ground view.
In the front view, A2 is the point on one branch of the intersection hyperbola located in the greatest distance from the ground image plane,
B2 is the point on the other branch of the intersection hyperbola located in the smallest distance from the ground image plane.
Ground view of the conical surface vertex is the focus of the intersection hyperbola ground view.
Other points located on the intersection hyperbola, K, K´, L, L´ are located on circles k, k´
and on the trace pa and
principal line of the first frame in the intersection plane.
All points of the intersection hyperbola located on one branch are visible in the ground view, while the other branch is entirely invisible.
In the orthogonal axonometry on the obr. 2.82, the hyperbolic intersection on the conical surface of revolution by the plane a perpendicular to the front image plane is illustrated.
Tangent point E of the intersection hyperbola axonometric view to the surface outline can be determined on this line in the front view, where the intersection plane appears in the edge view.