CURVES in the PLANE

1. Line segment

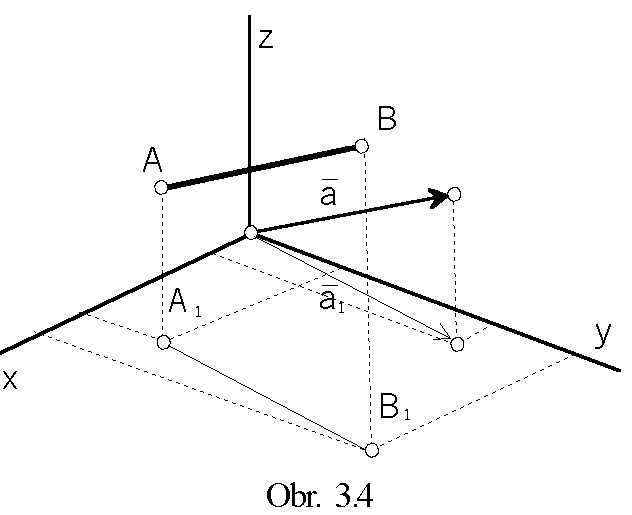
Line segment can be created by translating a given point in the direction of a given vector (Fig. 3.4).

Synthetic representation:      (A, T_p(u))

Analytic representations:

basic figure - A=(x_A, y_A, z_A,1)

generating principle - class of translations determined by the vector
                                a=(a₁, a₂, a₃, 0)

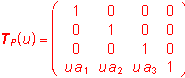    , for uÎ<0,1>

modelled figure - r(u) = A.T_P(u) =(x_A + ua₁, y_A+ ua₂, z_A+ ua₃,1), uÎ<0,1>

Interior properties of the modelled figure:

r´(u) = (a₁, a₂, a₃, 0)      

r´´(u) = 0       r´(u) ´ r´´(u) = 0        çr´(u) ´ r´´(u)ç = 0       r´´´(u) = 0

Frenet-Serret trihedron in the point P(u), uÎ<0,1> does not exist.

           b(u)=0           n(u)=0

¹k(u)=0           ¹r=           ²k(u)=0

All points on the line segment are points of inflection, any plane passing through the line segment is the osculating plane.
Line segment (line) is the curve of zero both, the first and the second curvatures.

2. Circular arc (circle)

Circular arc can be created by revolving the point about the line o by angles from the interval <0,a>.
For a=2p there is created the circle (Fig. 3.5).

Synthetic representation:      (A, T_Oz(u))

Analytic representations:

basic figure - A=(a, 0, 0, 1), a 0

generating principle - class of revolutions about the coordinate axis z
                                 by angles from the interval <0,a>

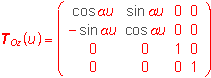•     , for uÎ<0,1>

modelled figure - r(u)=A.T_Oz (u)=(acos au, asin au, 0, 1)

u Î<0,1>, a 0 is the diameter of the circle

Interior properties of the modelled figure:

r´(u)=(-asin au, acos au, 0, 0)    ç r´(u)ç =

r´´(u)= -a²( acos au, asin au, 0, 0)

r´´´(u)= -a³(-asin au, acos au, 0, 0)

r´(u) ´ r´´(u) = (0, 0, a³a², 0)             ç r´(u) ´ r´´(u)ç = a³a²             [r´(u) r´´(u) r´´´(u)]=0

Frenet-Serretov trihedron in the point P(u), u Î<0,1>

t(u)= (-sin au, cos au, 0, 0)             b(u)=(0, 0, 1, 0)             n(u)= ( -cos au, -sin au, 0, 0)

¹k(u)=1/a             ¹r(u)=a             ²k(u)=0

Circle is a curve in the plane, which is self-osculating circle at any point, radius of the circle is the radius of the first curvature.

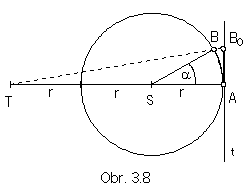
Rectification methods of the circular arc length

Kochański (central angle of the arc AB is about 180°)

(Fig. 3.6)

1. AÎt, t ^ AB

2. | AST|=30°, |TA₀|=3.|SA|=3a

3. |AB|=|A₀B|=pa

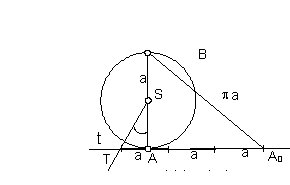
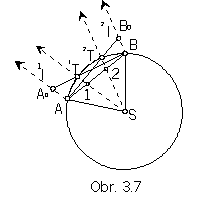D'Ocagne (central angle of the arc AB is in the interval (30°, 60°))

(Fig. 3.7).

1. |A1|=|12|=|2B|

2. S1ÇAB=¹T       (S2ÇAB=²T)

3. Aιl, ¹l // S1       (Bβl, ²l // S2)

4. ¹lÇB¹T=A₀, |A₀B|=|AB|        (²lÇA²T=B₀, |AB₀|=|AB)

Sobotka (central angle of the arc AB is in the interval (0°, 30°),
(obr. 3.8.)

1. AÎt, t ^ AS

2. |AT|=3.|AS|

3. TBÇt=B₀, |AB₀|=|AB|

3. Ellipse

Ellipse can be created as the affine image of the circle (Fig. 3.9).

Synthetic representation:     (k,T_A)

Analytic representations:

basic figure - circle k

q(u)=(acos au, asin au, 0, 1)

uÎ<0,1>, a=2p for the whole ciorcle, a 0

generating principle - axial affinity with axis in the coordinate axis x and the pair of corresponding points

                (0, a, 0, 1)®(0, b, 0, 1) in the direction of the vector s=(0, b-a, 0, 0), b 0

modelled figure - r(u) = q(u).T_A =(acos au, bsin au, 0, 1)

uÎ<0,1>, a=2p for the whole ellipse, a>b, a is the major axis, b is the minor axis

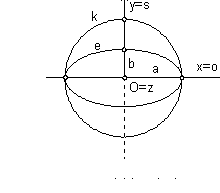
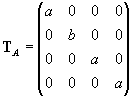
Interior properties of the modelled figure:

r´(u)=a(-asin au, bcos au, 0, 0)      çr´(u)ç =a

r´´(u)= -a²(acos au, bsin au, 0, 0)      r´´´(u)= -a³(-asin au, bcos au, 0, 0)

[r´(u) r´´(u) r´´´(u)]=0     r´(u) ´ r´´(u) = (0, 0, a³ab, 0)     çr´(u) ´ r´´(u)ç =a³ab

Frenet-Serretov trihedron in the point P(u), uÎ<0,1>

t(u)=(-asin au, bcos au, 0, 0)/d     b(u)=(0, 0, 1, 0)     n(u)= (bcos au, -asin au, 0, 0)/d

¹k(u)=ab/d^{3     1}r(u)=d³/ab     ²k(u)=0

4. Parabola

Parabola can be created as the collinear image of the circle (Fig. 3.10).

Synthetic representation:       (k, T_K)

Analytic representations:

basic figure - circle k

q(u)=(acos au, asin au, 0, 1)

uÎ<0,1>, a 0, a=2p for the whole circle

generating principle - central collineation
with the axis in the coordinate axis x,
centre S=(0, s, 0, 1)
and pair of corresponding points

U=(0, a, 0, 1)® U´=(0, a-s, 0, 0), s 0

modelled figure

r(u)=q(u).T_K=(acos au, (a-s)sin au, 0, 1-sin au)=
uÎ<0,1> -1/4, a=2p for the whole parabola, a= -p for the arc AB

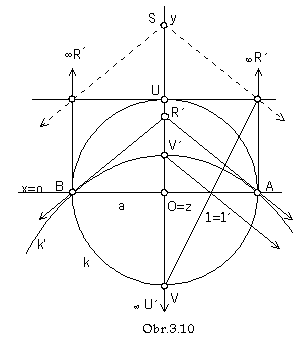
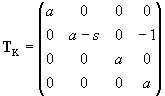
Ideal point of the parabola is the point P(1/4).

Point V=(0, -a, 0, 1) is mapped to the vertex of parabola
V´=V.T_K=(0, s-a, 0, 2)=(0, (s-a)/2, 0, 1)=r(3/4)=

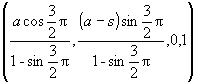
Ideal point R of intersection of tangent lines to the circle k in its invariant points A, B is mapped to the real point R´,
in which the tangent lines to the collinear parabola k´intersect.

5. Hyperbola

Hyperbola can be created as the collinear image of the circle (Fig. 3.11).

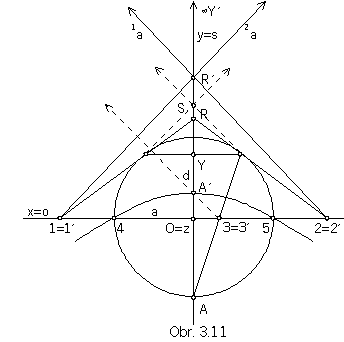
Synthetic representation: (k, T_K)

Analytic representations:

basic figure - circle k

q(u)=(acos au, asin au, 0, 1)

uÎ<0,1>, a 0, a=2p for the whole circle

generating principle

central collineation with the axis in the coordinate axis x,
centre S=(0, s, 0, 1)
and pair of corresponding points

Y=(0, d, 0, 1)® Y´=(0, d-s, 0, 0), d<a, d 0, s 0

modelled figure

r(u)=q(u).T_K=(adcos au, a(d-s)sin au, 0, -asin au+d) =

uÎ<0,1> - {u₁, u₂}, .

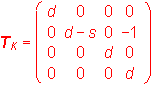
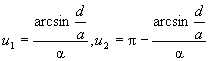Ideal points on hyperbola are P(u₁), P(u₂).
Point A=(0, -a, 0, 1) is collinearly mapped to the vertex of hyperbola ,
point B=(0, a, 0, 1) to the other one (not viewed) vertex .