Axonometria je rovnobežné premietanie na jednu priemetňu (axonometrická priemetňa ρ - nesplývajúca so žiadnou zo súradnicových rovín π, ν, μ),
pričom do tejto priemetne premietame priestorové útvary aj ich priemety do súradnicových rovín (príp. celý súradnicový trojhran Ox⁺y⁺z⁺).
Ak je smer premietania s kolmý na axonometrickú priemetňu ρ, hovoríme o kolmej axonometrii.
Axonometrická priemetňa ρ pretína všetky súradnicové roviny,
ρ ∩ π =XY, ρ ∩ ν =XZ, ρ ∩ μ =YZ (obr. 1.41).
Trojuholník XYZ, ktorého vrcholy sú priesečníky axonometrickej priemetne ρ postupne so súradnicovými osami x, y, z, nazývame axonometrický trojuholník (alebo aj Pelcov stopný trojuholník).
Kolmým priemetom súradnicových osí x, y, z do axonometrickej priemetne ρ sú priamky x_A, y_A, z_A, ktoré sú výškami axonometrického trojuholníka XYZ.
Kolmým priemetom začiatku súradnicovej sústavy O do ρ je ortocentrum trojuholníka XYZ. Útvar O_ax_ay_az_a nazývame axonometrický osový kríž.
Posúvaním axonometrickej priemetne ρ v smere s meníme veľkosť axonometrického trojuholníka XYZ (vzdialenosť ρ od začiatku O), ale priemet axonometrického osového kríža sa nemení (obr. 1.42).
Všetky stopné trojuholníky sú navzájom rovnoľahlé so stredom rovnoľahlosti v bode O a určujú tú istú axonometriu. V kolmej axonometrii je axonometrický trojuholník XYZ vždy ostrouhlý.

Bod A priestoru kolmo premietneme do pôdorysne do bodu A₁.
Kolmý priemet A_a bodu A do axonometrickej priemetne ρ - axonometrický priemet
a kolmý priemet A_1a pôdorysu A₁ do axonometrickej priemetne ρ - axonometrický pôdorys,
sú dvojicou axonometrických priemetov bodu A, združených v smere priemetu osi z kolmom na stranu XY axonometrického trojuholníka.
Ak je nákresňou axonometrická priemetňa, vynecháme označenie axonometrických priemetov, index "a" (obr. 1.43).

Bod A je jednoznačne určený dvojicou svojich axonometrických priemetov (A, A₁).
Obdobne možno bod A priestoru určiť dvojicou axonometrických priemetov (A, A₂) - axonometrický priemet a axonometrický nárys, príp. (A, A₃) - axonometrický priemet a axonometrický bokorys.
Axonometrický pôdorys a axonometrický priemet pôdorysne splývajú (axonometrická priemetňa), axonometrický nárys pôdorysne je v priemete osi x a axonometrický bokorys v priemete osi y (obr. 1.44).
Všetky body pôdorysne majú totožný axonometrický priemet a axonometrický pôdorys, P = P₁.
Rovnako platí pre body nárysne N = N₂, axonometrický pôdorys nárysne je v priemete osi x a axonometrický bokorys v priemete osi z.
Axonometrický pôdorys bokorysne je v priemete osi y, axonometrický nárys v priemete osi z a M = M₃ pre každý bod bokorysne.

Roviny π, ν, a μ rozdelia priestor na osem oktantov (obr. 1.45):

I. x > 0, y > 0, z > 0                              V. x > 0, y > 0, z < 0

II. x > 0, y < 0, z > 0                              VI. x > 0, y < 0, z < 0

III. x < 0, y < 0, z > 0                              VII. x < 0, y < 0, z < 0

IV. x < 0, y > 0, z > 0                              VIII. x < 0, y > 0, z < 0

Útvary zobrazujeme v axonometrii s viditeľnosľou vzhľadom na I. oktant, trojhran Ox⁺y⁺z⁺, uplatnenou len na axonometrický priemet.

Ak súradnicové osi x, y, z zvierajú s axonometrickou priemetňou ρ rôzne uhly, potom dĺžky priemetov jednotkových úsečiek j_x, j_y a j_z na osiach sú rôzne,
axonometrický trojuholník XYZ je rôznostranný a axonometriu nazývame trimetria (obr. 1.46a).

Ak sú uhly dvoch súradnicových osí s axonometrickou priemetňou ρ zhodné, jednotkové úsečky na týchto osiach sa premietajú ako rovnako dlhé úsečky,
axonometrický trojuholník je rovnoramenný a axonometriu nazývame dimetria (obr. 1.46b).

Ak sú uhly všetkých osí x, y, z s axonometrickou priemetňou ρ zhodné, priemety jednotkových úsečiek sú na všetkých osiach rovnako dlhé,
axonometrický trojuholník je rovnostranný a axonometria sa nazýva izometria (obr. 1.46c).

Nech je daná všeobecná axonometria určená priemetňou ρ a smerom premietania s, s ∉ ρ.
Čísla p, q, r udávajúce pomery dĺžok priemetov jednotkových úsečiek j_x, j_y, j_z na súradnicových osiach ku jednotke dĺžky j

nazývame koeficienty zmeny (skrátenia alebo predĺženia na axonometrických osiach).
Pre koeficienty zmeny platí:

p² + q² + r² = 2 + cotg² φ, φ = ∡ s ρ

kde φ je uhol smeru premietania s priemetňou. Pre kolmú axonometriu (s ⊥ ρ, φ = 90° ) je p² + q² + r² = 2.

Na technických výkresoch, na ktorých podstatnú zložku tvoria pôdorysy, príp. bokorysy a priečne rezy zobrazovaných útvarov, sa často používa šikmé axonometrické zobrazenie.

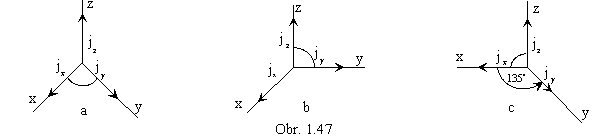
Vojenská perspektíva je zobrazenie vhodné na technické výkresy používané v urbanizme pri návrhu sídlisk a zostrojovaní priemetov objektov s komplikovaným pôdorysom a zložitou stavbou.
Priemety súradnicových osí x a y sú kolmé, a platí p : q : r = 1 : 1 : 1, čiže j_x = j_y = j_z = kj, k > 0 (obr. 1. 47a).

Kavalierna perspektíva je šikmé premietanie, v ktorom sa premieta do roviny rovnobežnej s nárysňou alebo bokorysňou.
Používala sa už v 16. a 17. storočí pri zhotovovaní plánov (tzv. vedút) dôležitých miest a sídlisk.
Priemety súradnicových osí x a z, príp. y a zsú kolmé, a p : q : r = 1 : 1 : 1, j_x = j_y = j_z = kj, k > 0 (obr. 1. 47b).

Obe spomenuté zobrazenia sa používali na vojenské účely, praktickosť konštrukcií prevláda nad dobrou názornosťou, a v oboch platí φ = 45°.

Šikmé premietanie je najnázornejšie zobrazenie najčastejšie používané na technických výkresoch v strojárenstve.
Priemety súradnicových osí x a z, príp. y a z sú kolmé, a pomer koeficientov zmeny je 1 : q : 1, príp. p : 1 : 1 (pričom q, príp. p je z intervalu (0, 1)).
V tzv. technickom premietaní sa orientovaný uhol priemetu súradnicovej osi y s priemetom súradnicovej osi x rovná 135 °, j_y = (obr. 147c).