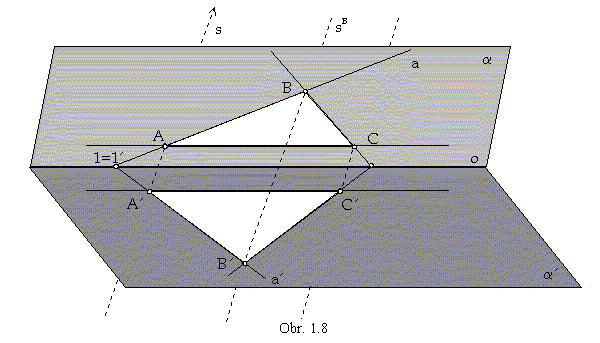
Line s=AA' is the direction of affinity s (obr. 1.8).
Affine transformation, with the invariant figures in
Axial affinity is determined unambiguously by the axis o and a pair of corresponding points
A and A' (a=oA, a'
=oA').
Line s=AA' is the direction of affinity s (obr. 1.8).

Image of an arbitrary point B Îa is the point B' Îa', which can be determined with respect to the following rules:
1. Point B' is located on the line sB from the pencil of lines in the direction of affinity s passing through
the point B
B'ÎsB
|| s. All lines passing through the pairs of corresponding points are in the pencil of lines determined by the direction s
AA' || BB' || CC' || ... || s.
2. Any line in the plane a intersects the axis of affinity o in its invariant point,
which must be located also on its affine image.
If the image of line a is the line a'
Îa', then aÇ
a'=1=1', where 1
=1'Îo.
Let a=AB, the affine image a' of this line must be
passing through the point 1=1' on the axis of affinity.
Lines in the direction of the axis of affinity have ideal invariant points.
3. Axial affinity keeps invariant the incidence of points and lines, the image of a line a=AB
must be line a'=A'B', determined
by its two different points
A' and 1=1'. Affine image of the point B is the point B'
=a'Ç sB.
Projecting the pair of affinely corresponding planes a, a'
and the direction of affinity s on the plane,
while none of the planes a,
a' appears in the edge view as a line,
and views of the direction s =
AA' and the axis of affinity o are two intersecting lines,
an axial affinity in the extended Euclidean space ![]() E2
can be obtained.
E2
can be obtained.
It is determined by the invariant axis of affinity (view of the intersection line o=aÇa')
and a pair of corresponding points (views of points AÎa,
A'Îa') in the direction of affinity
(view s=AA') (obr 1.9).
Due to a described algorithm the affine image B' of an arbitrary point B in the plane can be constructed.
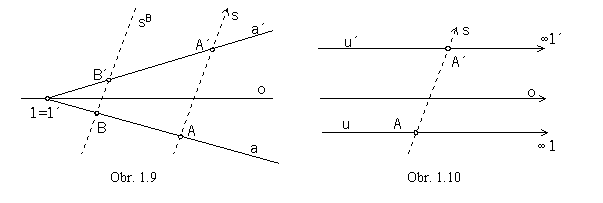
Line u in the direction of affinity passing through the point A has the ideal invariant point
![]() 1,
1,
which is also the point of its image u'.
In the point A' (image of the point A) the line u' in the direction of the axis of affinity o is located (obr. 1.10).
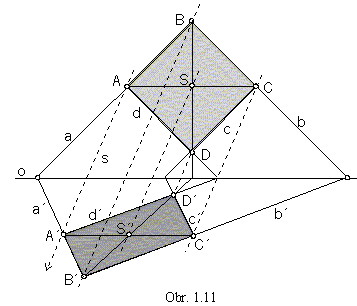
Two lines (b || d) in the same direction are mapped in the axial affinity into two lines in the same direction
(b' || d'), intersecting lines (a´b) are mapped to intersecting lines
(a'´b'), while the intersection point of the line images (B') is the image of the
intersection point of the original lines (B).
Centre (S) of a geometric figure is mapped to the centre (S') of the figure image.
Size of angles and length of line segments are not invariant in the axial affinity (obr. 1.11).
On lines in the same direction the same scaling ratio is applied, line segments are shortened or lengthened in the same ratio
(|AD|=|BC|, |A'D'|=|B'C'|).
Line segment length is invariant on lines in the direction of the axis of affinity, only (|AC|
=|A'C'|).
Affine image of a circle is an ellipse (or a circle, in a particular case).
Let the axial affinity A be determined by the axis o and a pair of corresponding points O and O'.
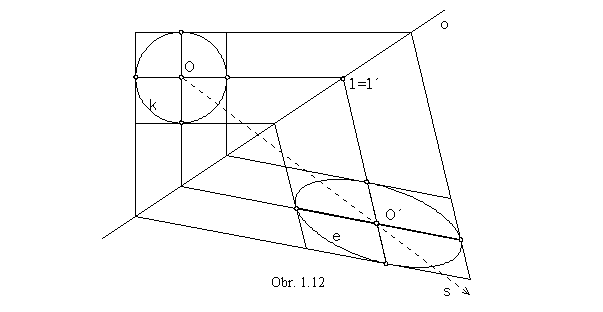
A ={o, O® O', s =OO'}
Image of the circle k with the centre O is an ellipse e with the centre O'. Any two orthogonal diameters of the circle k are affinely mapoped to the related (comjugate) diameters of the ellipse e (obr. 1.12).
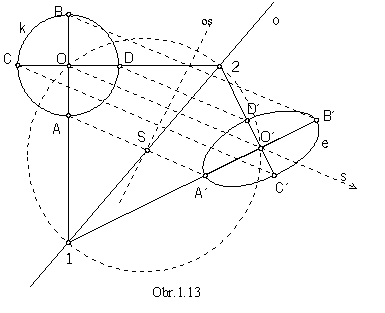
There exists a pair of orthogonal diameters AB![]() CD of the circle,
which are mapped affinely to the axes of the ellipse passing through the vertices A'B'
CD of the circle,
which are mapped affinely to the axes of the ellipse passing through the vertices A'B'![]() C'D'.
C'D'.
Invariant points of these diameters are located on the circle of Thales passing through the centres of the affinely
corresponding curves.
Points O and O' are vertices of the rightangled triangles with the common hypotenuse, line segment 12 (obr. 1.13) on the axis of affinity o.
Centre of the circle of Thales is the point S, intersection point of the line segment OO' axis and the axis of affinity
o.
There exists an axial affinity attached to an arbitrary ellipse, while the image of the ellipse is a circle.
Ellipse determined by the major vertices, e=(AB![]() CD)
CD)
1A= {1o=AB, C ®1C}, 2 A={2o =AB, C ®2C} (obr. 1.14)
Ellipse determined by the conjugate diameters, e=(PQ, RS)
1A= {1o=PQ, R ®1R}, 2A ={2o=PQ, R ®2R} (obr.1.15)


A = {A® A', B ®B', C ®C'}, o=?
Solution:
Line AB is mapped in the given axial affinity to the line A'B'.
Intersection point of these lines is the invariant point on the axis of affinity, ABÇ
A'B'={1=1'},
axis of affinity o is passing through this point.
The same is true for the invariant point of lines AC and A'C' ,
ACÇ
A'C'={2=
2'}Îo.
Axis of affinity is the line o=12 (obr. 1.16).
Problem 1.2: Find tangent lines to the ellipse parallel to the given line m, while the ellipse is determined by vertices.
e=(AB![]() CD),
1t=?, 2t=?
CD),
1t=?, 2t=?
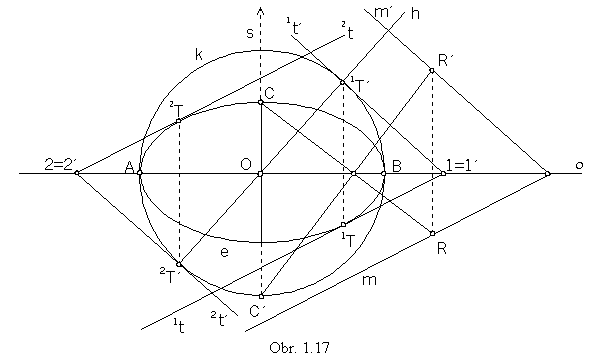
Solution:
In the axial affinity A={o=AB, C®C'}
the given ellipse e is mapped to the circle k,
while the direction of affinity is perpendicular to the axis of affinity.
Line m is affinely mapped to the line m', determined by the invariant point on the axis of affinity
and image R' of one point R on the line m
(R' can be determined by the direction of affinity and the image of line RC).
Tangent lines to the circle k, which are parallel to the line m', can be constructed easily,
tangent points 1T', 2T' are intersection points of the line h located in the centre O
of the circle
and perpendicular to the line m', 1T'Î
1t'|| m', 2T'
Î2t'||
m'.
Affine images of lines 1t' and 2t' can be determined by their invariant points
on the axis of affinity
and by their direction, 1=1'
Î1t||
m, 2=2'Î2t
|| m.
Tangent points 1T
Î1t and 2T
Î2t are located on lines in the direction of affinity (obr. 1.17).