Central collineation of the plane a on the plane a'

Projective transformation, with the set of invariant points in

- the point invariant real line, axis of collineation o=aÇa'
- one real point in the space, centre of collineation S not located in any of the planes a and a'
- and a set of invariant lines (not point invariant) passing through the common point S is a central collineation (obr. 1.18).

It is determined unambiguously by the axis o, a pair of corresponding points A, A' (a = oA , a' = oA') and a centre S located on the line determined by this points, S Î AA'.

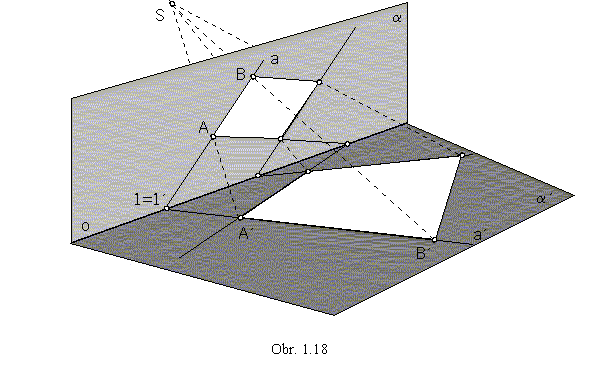
Image of an arbitrary point B in the plane a is the point B' in the plane a', which can be determined due to the following rules:

1. All pairs of points corresponding in the central collineation form lines passing through the centre of collineation S,
AA' Ç BB' Ç ... =S, B' ÎBS.

2. Any line in the plane a intersects the axis of collineation o in its invariant point, located also on the collinear image of the line. If the image of the line a in the plane a is the line a' in the plane a', then aÇa'=1=1', 1=1'Îo.
Let a=AB, the image a' of this line must be passing through the point 1=1' on the axis of collineation.

3. With respect to the invariant incidence, the image of the line a=AB is the line a'=A'B', which is determined by its two different points A' and 1=1'. Then B'=BS Ça'.

Projecting the two collinearly corresponding planes a and a' and the centre of collineation S on the plane, while none of the planes appears in the edge view and the view of the point S is a real point not located on the view of the axis of collineation o, central collineation in the extended Euclidean plane E2 can be obtained.
It is determined by the axis of collineation in the view of the intersection line o=aÇa', by the centre in the view of the centre of collineation S not located on the axis o, and a pair of corresponding points in the views of points AÎa, A'Îa' , SÎAA', (obr. 1.19). Collinear image B' of an arbitrary point B in the plane can be determined due to the described algorithm.


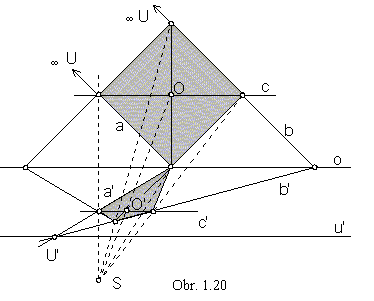
Central collineation is a linear transformation mapping ideal points in the extended Euclidean plane to the real points (obr. 1.20).
Two lines of the same direction (a||b) are mapped to the two intersecting lines (a'´ b'), while their common invariant ideal point U is mapped to the real point U', intersection point of the images of lines (U'=a' Çb').
Lines in the direction of the axis of collineation are mapped to the lines in the same direction of the axis of collineation (c||c'||o).
Image of the ideal line u in the plane is a real line u' in the direction of the axis of collineation, called neutral line.
Centre of a geometric figure O is not mapped to the centre O' of the figure image.

Collinear image of a circle can be in the form of a conic section - ellipse, parabola, hyperbola (circle including).
Set M of all points on the circle, which are mapped in the given central collineation to the ideal points, is the set of all intersection points of the circle and the neutral line.



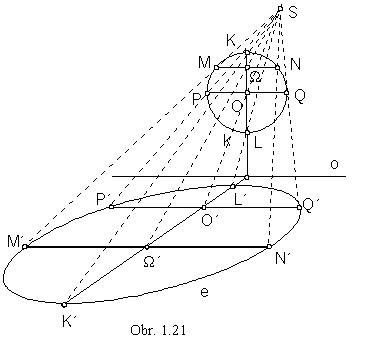
Collineation correspondence between a circle and an ellipse

K ={S, o, O®O'}, kÇu =M =Æ, k®e=?

When all points on the circle are mapped to the real points (neutral line has no commonon points with the circle), the collinear image of the circle is an ellipse (obr. 1.21).
Centre O of the circle k is mapped to the interior point O' of its image, ellipse e.
Diameter KL of the circle, which is perpendicular to the axis of collineation, and the chord MN parallel to the axis of collineation o are collinearly mapped to the conjugate diameters K'L' and M'N'||o of the ellipse with the common point W' in the centre of the ellipse. Diameter PQ||o corresponds to the chord P'Q'||o of the ellipse .
(Rytz method of construction can be used to determine the axes and semiaxes of the ellipse e.)


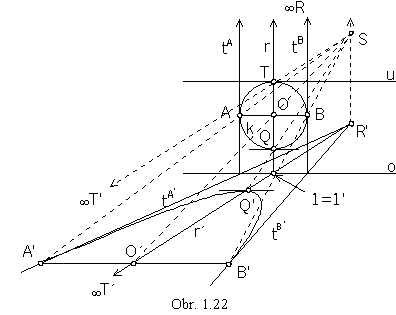
Collineation correspondence between a circle and a parabola

K ={S, o, T ® T'}, TÎu||o, kÇ u=M={T}, k®p=?

When the only one point of the circle is mapped to the ideal point (neutral line is tangent to the circle in this point), the collinear image of the circle is a conic section with one ideal point, a parabola (Obr. 1.22).
Diameter r of the circle k passing through the point T perpendicularly to the axis of collineation is mapped to the line r' (determined by the direction T' and invariant point 1=1'), which is in the direction of the collinear parabola p axis. On this line the parabola point Q', image of the point Q on the circle, is located. Tangent line to the parabola in the point Q' is in the direction of the axis of collineation.
Diameter AB of the circle, AB || o and tangent lines tA, tB in the points A, B correspond collinearly to the chord A'B' || o passing through the point O'Îr' (image of O) and to the tangent lines to the parabola tA', tB' passing through their invariant points on the axis of collineation o. Two tangent lines with the tangent points determine the parabola unambiguously, using the definition of parabola and known size of the tangent points A, B focal distances, the focus, directrix and vertex of parabola can be determined.

Collinear correspondence between a circle and a hyperbola

K ={S, o, U® U'}, UÎ u || o, kÇu=M ={U, V}, k®h=?

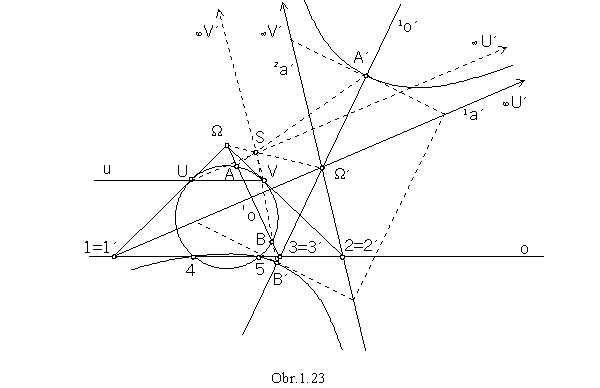
When two different points U, V on the circle are mapped to the ideal points (neutral line intersects the circle in these two points), the image of the circle is a conic section with two ideal points, a hyperbola (obr. 1.23).
Tangent lines to the hyperbola in its ideal points are asymptotes, they must be collinear images of the tangent lines to the circle k in the points U, V. Their intersection point W is mapped to the centre of the hyperbola W'.
Axis of the angle of asymptotes 1a' and 2a' is the axis of the hyperbola 1o', it is the collinear image of the line 1o=3W. Intersection points A, B of this line and the circle are mapped to the hyperbola major vertices A', B'.
Hyperbola minor vertices and foci can be determined from the hyperbola characteristic rectangular.
Circle and hyperbola intersect in the invariant points 4 and 5 on the axis of collineation.

Problem 1.3: Find the image of the triangle DABC in the central collineation K ={S, o, U® U'}, (obr. 1.24).

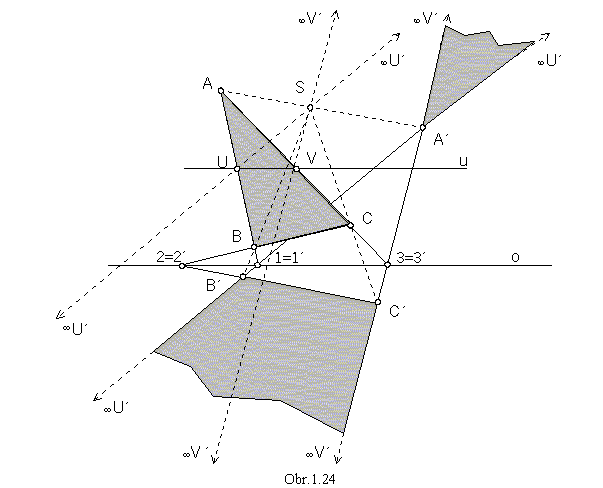
Solution: Invariant point 1=1' on the line AB and the direction of the ideal point U' determine the collinear image of the line AB, on which points A' and B' are located, while A'Î AS, B'ÎBS. The ideal point U' is located on the line segment A'B', and therefore its image splits to a pair of half-lines. Image of the line BC, determined by the invariant point 2=2' and the point B', intersects line SC in the point C'. The ideal point V' is located on the line segment A'C', it is the collinear image of the point V, the intersection point of the line segment AC and the neutral line u passing through the point U and parallel to the axis of collineation. Image A'B'C' of the triangle ABC in the given central collineation splits to two parts sharing a common ideal line segment U' V' on the ideal line of the plane .