3. ZÁKLADY PREMIETANIA PRIESTORU DO ROVINY
Špeciálne zobrazenie priestoru na zvolenú rovinu - nákresňu nazývame premietanie.
Poznáme dva základné druhy premietania, stredové a rovnobežné.
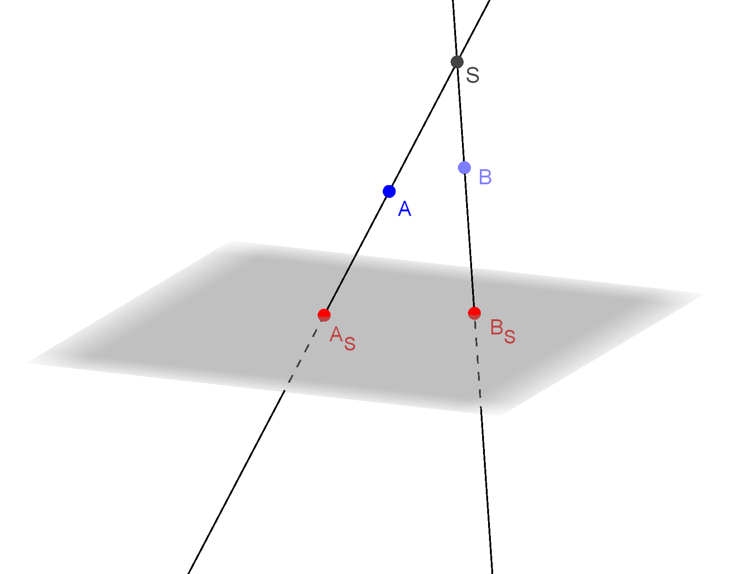
Stredové premietanie
Zvolený je pevný bod S ∈ E3
ktorý neleží v nákresni - zvolenej rovine π (priemetňa).
Obrazom každého bodu A ∈ E3, A
ktorý je priesečníkom premietacej priamky AS prechádzajúcej bodom A a stredom premietania S
s priemetňou, AS = SA ∩ π . Vzdialenosť stredu premietania od priemetne nazývame dištancia, | S π | = d.
Stred premietania nemá priradený obraz - priemet.
Stredové premietanie nezachováva rovnobežnosť,
ani deliaci pomer bodov na priamke.
Špeciálne stredové premietanie, pri ktorom sú zobrazované objekty umiestňované do zorného kužeľa, sa nazýva lineárna perspektíva.
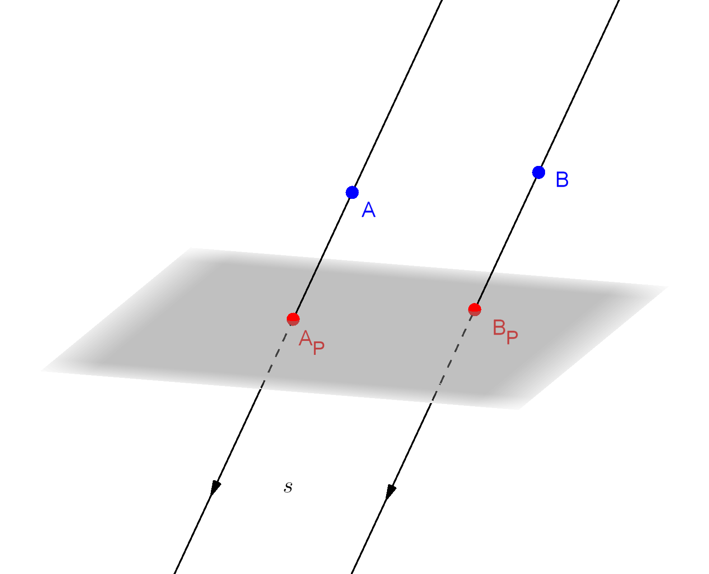
Rovnobežné premietanie
Daný je smer premietania s, osnova rovnobežných priamok priestoru E3,
ktorý nie je rovnobežný s nákresňou - zvolenou rovinou π (priemetňa).
Obrazom ľubovoľného bodu A ∈
E3
je bod AP ∈ π, ktorý je priesečníkom
premietacej priamky sA, A ∈ sA
zo smeru s prechádzajúcej bodom A s priemetňou,
AP = sA ∩ π.
Stredové ani rovnobežné premietanie nie je jedno-jednoznačným zobrazením priestoru
E3 na rovinu.
Všetky body každej premietacej priamky sa zobrazia do toho istého bodu, priesečníka s priemetňou.
Všetky body priemetne sú pri oboch premietaniach samodružné.
Priemetom geometrického útvaru je útvar, ktorý získame ako množinu priemetov všetkých jeho bodov.
Priemetom priamky, ktorá nie je premietacou priamkou, je priamka. Priemetom premietacej priamky je bod.
Množina všetkých premietacích priamok bodov jednej priamky vytvára premietaciu rovinu priamky.
Priemet priamky je priesečnica premietacej roviny priamky s priemetňou. Priemetom roviny, ktorá nie je premietacou rovinou, je celá priemetňa. Priemetom premietacej roviny je priamka.
Vlastnosti rovnobežného premietania:
1. Priemetom útvaru U, ktorý leží v rovine rovnobežnej s priemetňou, je útvar zhodný s útvarom U.
2. Rovnobežnosť je invariantom rovnobežného premietania.
Rovnobežné priamky nepatriace smeru premietania majú rovnobežné priemety.
3. Zachováva sa deliaci pomer bodov na priamke,
λ (ABS) =
λ (A1 B1 S1).
Stred útvaru sa premieta do stredu priemetu útvaru.
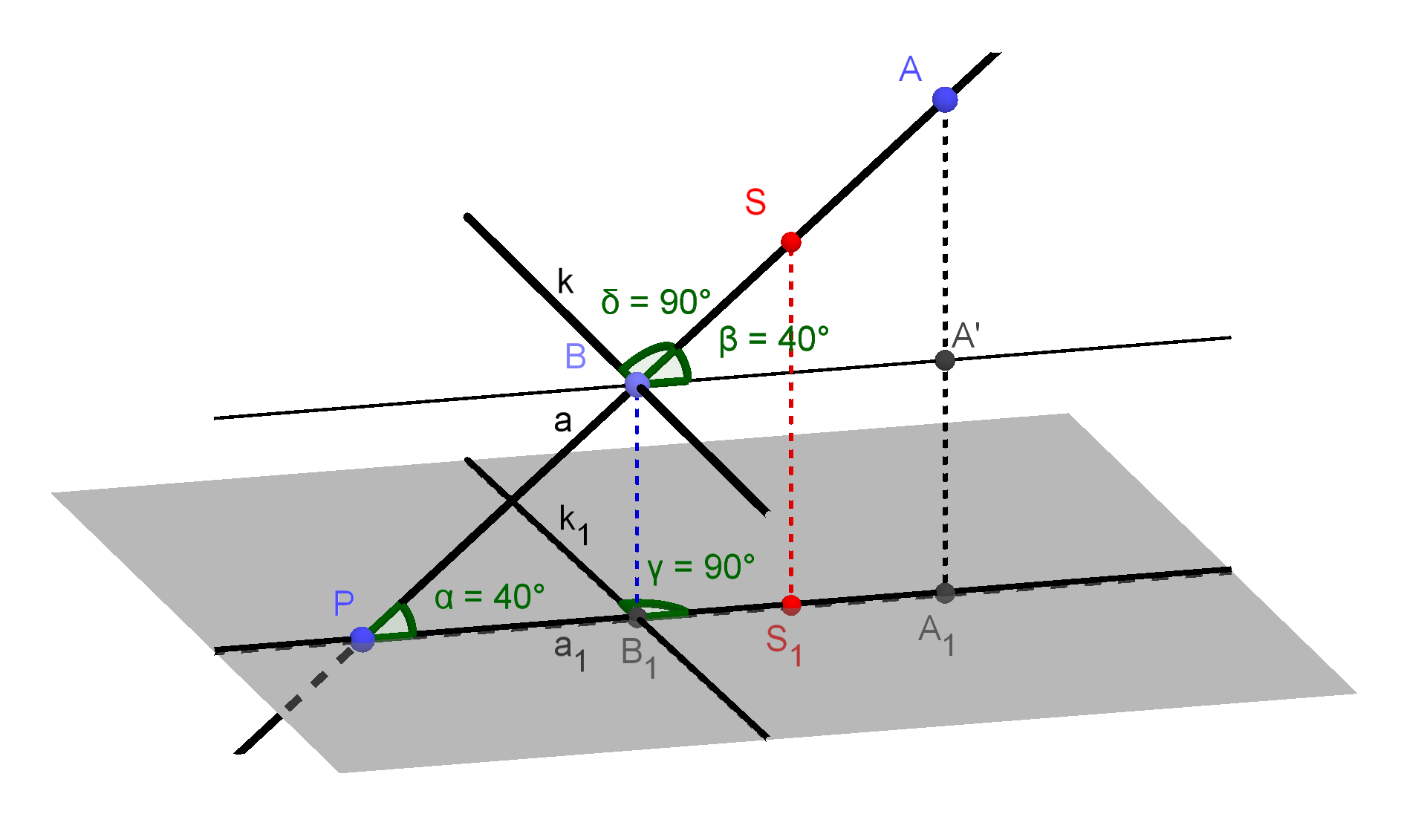
Kolmé premietanie je také rovnobežné premietanie, pri ktorom sú všetky premietacie priamky smeru s kolmé na priemetňu. Okrem vlastností rovnobežného premietania 1. - 3. platia ešte niektoré ďalšie.
4. Nech AB je úsečka na priamke a, ktorá zviera s priemetňou π uhol α . Pre kolmý priemet A1B1 platí
| A1 B1 | = | AB | cos α
Dĺžka kolmého priemetu úsečky je menšia (pre α ∈ ( 0°, 90° ),
pre α = 90° je A1 = B1),
alebo sa rovná (pre α = 0°) dĺžke danej úsečky AB.
5. Pravý uhol sa premieta ako pravý, ak je
aspoň jedno jeho rameno rovnobežné s priemetňou a ani
jedno nie je kolmé na priemetňu.
Úloha zobrazenia - premietania trojrozmerných objektov na rovinu vznikla z praktických potrieb človeka a má veľký význam v mnohých oblastiach. Pre technika však nestačí objekt len premietnuť, ale potrebuje z príslušného nákresu - obrazu objektu zistiť niektoré jeho vlastnosti, prípadne objekt jednoznačne zrekonštruovať. Táto úloha sa realizuje pomocou rôznych zobrazovacích metód.
Zobrazovacia metóda je bijektívne (prosté a na) zobrazenie bodov priestoru na rovinu. Najznámejšie zobrazovacie metódy sú: kótované premietanie, pravouhlé premietanie na dve navzájom kolmé priemetne (Mongeova projekcia), kolmá a šikmá axonometria, stredové premietanie a lineárna perspektíva, dvojstredové (stereoskopické) premietanie. Voľba vhodnej zobrazovacej metódy závisí účelu, ktorému má príslušný nákres slúžiť. V umení, architektúre a staviteľstve sa používa najmä lineárna perspektíva, príp. kótované premietanie, v strojárenstve sú najvhodnejšimí Mongeova projekcia a axonometria.
3.1. Lineárna perspektíva3.2. Mongeovo premietanie
3.3. Axonometria
3.4. Rekonštrukcia
3.5. Kolmé priemety rovinných útvarov
D. Velichová, 3D geometria