2. 1. Hilbertova axiomatická sústava

I. Axiómy incidencie

Opisujú relácie vzájomnej polohy bodov, priamok a rovín.

I₁: Dvoma rôznymi bodmi prechádza práve jedna priamka.

I₂: Každá priamka obsahuje aspoň dva rôzne body.

I₃: Existuje aspoň jedna trojica navzájom rôznych nekolineárnych bodov (neležia na jednej priamke).

I₄: Každé tri nekolineárne body obsahuje jediná rovina.

I₅: Každá rovina obsahuje aspoň jeden bod.

I₆: Ak dva rôzne body priamky ležia v rovine, tak v nej ležia všetky body tejto priamky.

I₇: Existuje štvorica bodov neležiacich v jednej rovine.

I₈: Ak dve rôzne roviny majú spoločný jeden bod, majú spoločnú priamku, ktorá týmto bodom prechádza.

II. Axiómy usporiadania

Vymedzujú základný vzťah "ležať medzi", ktorý označíme znakom λ. Skutočnosť, že bod C leží medzi bodmi A a B, budeme zapisovať symbolicky λ(ACB).

II₁: Ak platí λ(ACB), potom A, B, C sú navzájom rôzne body jednej priamky a platí aj λ(BCA).

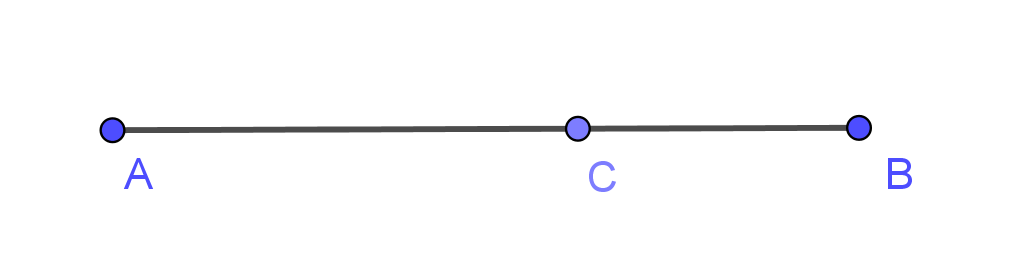
II₂: Ku každej dvojici rôznych bodov A, B existuje na priamke AB aspoň jeden taký bod C, že platí λ(ACB).

II₃: Z troch rôznych bodov A, B, C jednej priamky najviac jeden leží medzi zvyšnými dvoma, platí práve jeden zo vzťahov λ(ABC), λ(ACB), λ(CAB).

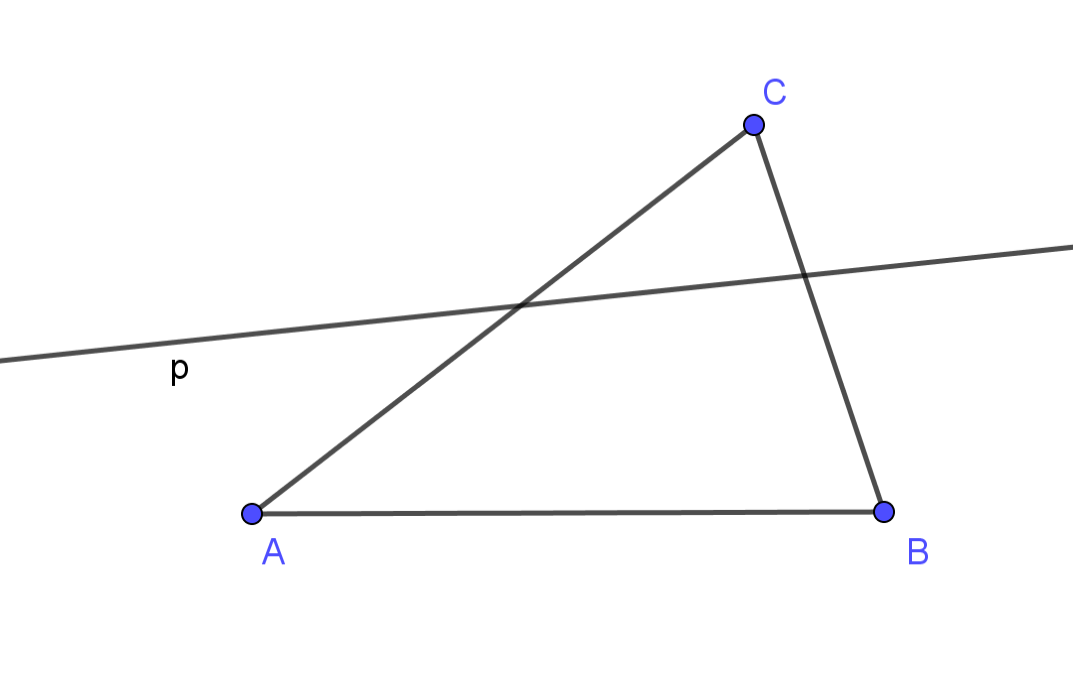
II₄: (Paschova axióma) Ak priamka p leží v rovine trojuholníka ABC, neprechádza ani jedným z jeho vrcholov a pretína jednu jeho stranu vo vnútornom bode, tak má spoločný bod ešte aspoň s jednou zo zvyšných dvoch strán trojuholníka (pretne ju vo vnútornom bode).

III. Axiómy zhodnosti

Opisujú zhodnosť úsečiek a uhlov, pomocou ktorej sa zavádza pojem zhodnosti aj pre ďalšie geometrické útvary. Ku každej dvojici úsečiek U₁, U₂ je priradený práve jeden z výrokov U₁ U₂ , U₁ ≇ U₂.

Ku každej dvojici uhlov pq, rs je priradený práve jeden z výrokov pq rs, pq ≇ rs.

III₁: Ak je U úsečka a p = OA polpriamka, ktorá má začiatok v bode O, potom na polpriamke p existuje taký bod A, že U OA.

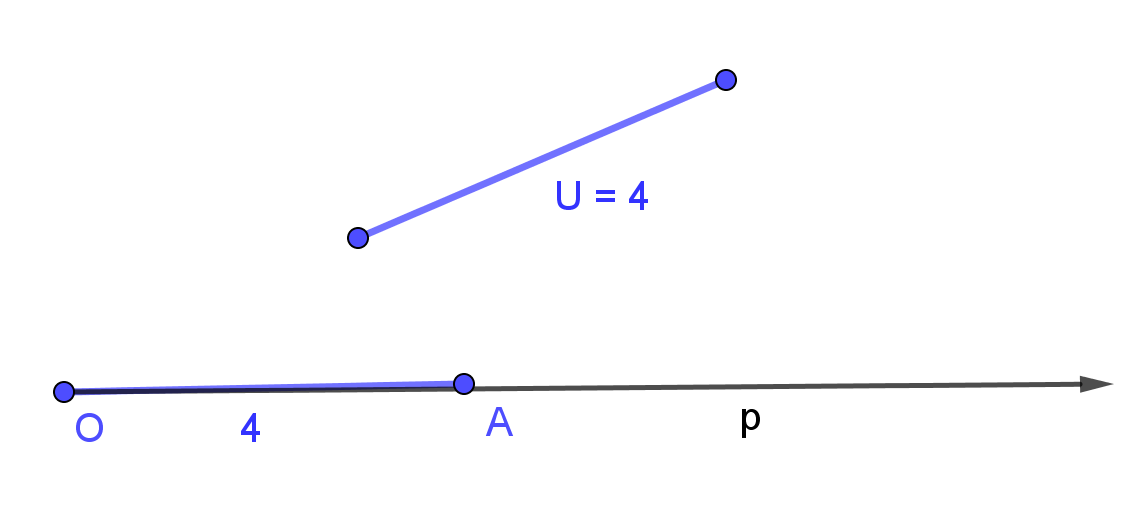
III₂: Pre každú úsečku AB platí AB BA.

Ak U₁ U₂, potom U₂ U₁. Ak U₁ U a U₂ U, potom U₁ U₂ .

III₃: Ak platí λ(ABC), λ(A'B' C') a AB A'B', BC B'C', potom AC A'C'.

III₄: Ak je daný pq a polrovina ( hA ) s hranicou h, na ktorej je zvolená polpriamka so začiatkom O, potom existuje práve jedna polpriamka so začiatkom v bode O a ležiaca v polrovine ( hA ) taká, že pq hk.

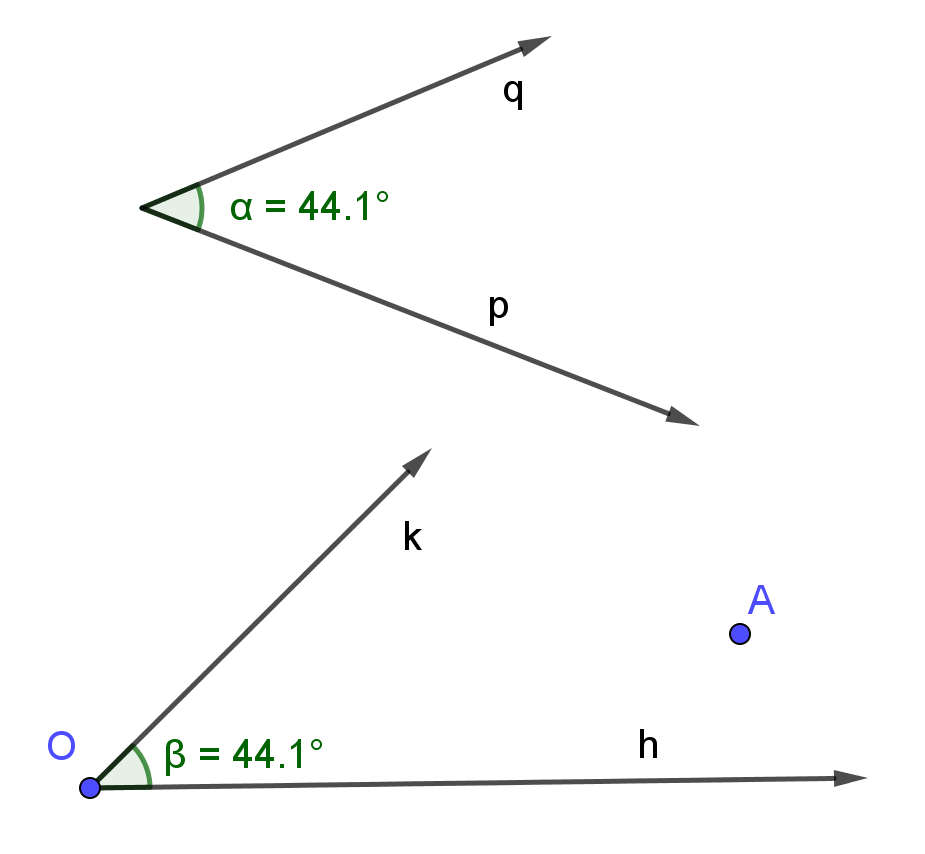
III₅: Pre každý uhol platí pq qp .
Ak platí pq rs , potom platí rs pq .
Ak pq rs a rs tv , potom pq tv .

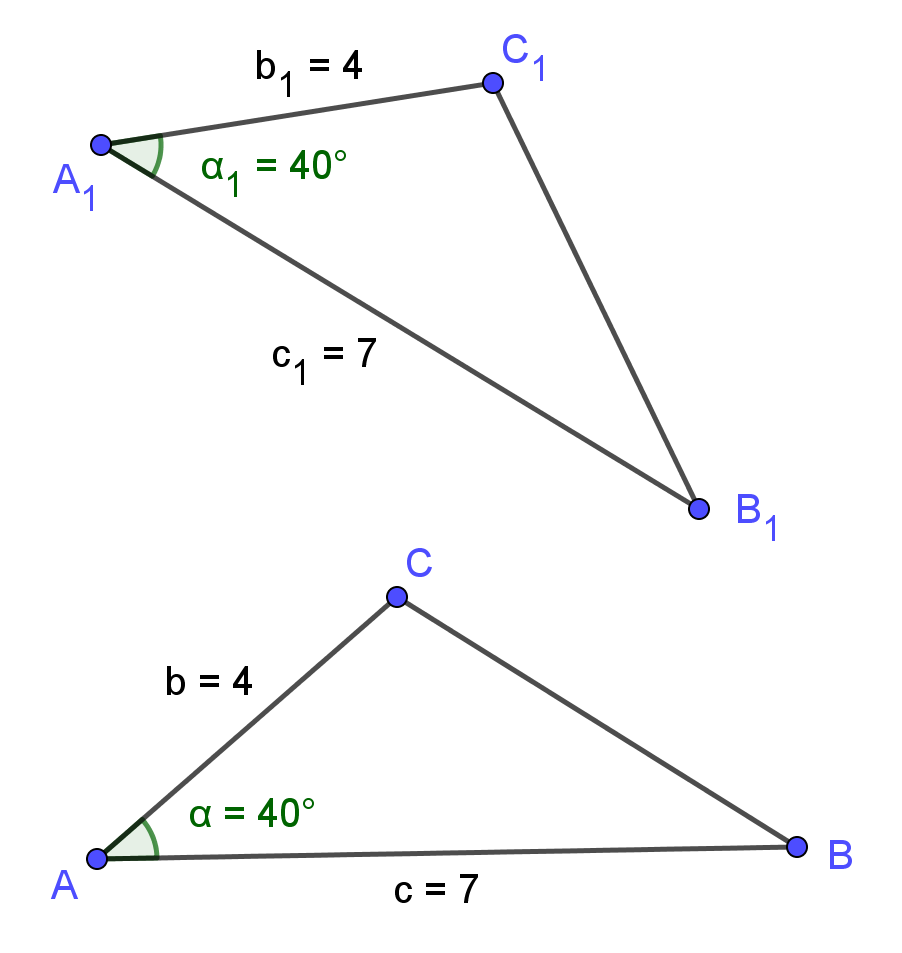
III₆: Nech sú dané dva trojuholníky ∆ABC, ∆A₁B₁C₁ a nech platí: AB A₁B₁, AC A₁C₁, BAC B₁A₁C₁. Potom ∆ABC ∆A₁B₁C₁.

IV. Axiómy spojitosti

Umožňujú meranie úsečiek, ktoré musí vyhovovať určitým prirodzeným požiadavkám. Dĺžka úsečky musí byť nezávislá od miesta, na ktorom sa meranie uskutočňuje a žiadna nesmie byť nulová alebo záporná. Úsečka sa musí dať odmerať po častiach, pričom jej dĺžka sa rovná súčtu dĺžiek čiastkových úsečiek. Musí existovať aspoň jedna úsečka jednotkovej dĺžky. Archimedova axióma je výsledkom veľkého množstva skúseností z rôznych meraní a zaručuje merateľnosť úsečiek. Každej úsečke možno priradiť reálne číslo, ktoré je jej dĺžkou. Nezaručuje však, že každé reálne číslo je dĺžkou aspoň jednej úsečky. Túto skutočnosť zaručuje Cantorova axióma.

IV₁: (Archimedov výrok)
Nech sú na priamke dané body A, A₁ a B také, že λ( A A₁ B ).
Ak na priamke definujeme postupnosť bodov A₁, A₂, ... , A_k-1, A_k, A_k+1, ... s podmienkami:
1. λ( A_k-1 A_k A_{k +1})
2. A_k A_k+1 AA₁
ktoré platia pre každé prirodzené číslo k, potom existuje prirodzené číslo n také, že neplatí λ( A A_n B ).

Archimedova axióma zaručuje existenciu miery úsečiek m(U) - funkcie definovanej na množine všetkých úsečiek so špecifickými vlastnosťami (kladná, aditívna, monotónna), ktorej obor hodnôt je množina nezáporných reálnych čísel. Každá úsečka, pre ktorú platí m(J)=1, sa nazýva jednotková úsečka (alebo jednotka) miery úsečiek m(U).

IV₂: (Cantorov výrok)
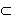Nech je na priamke p daná postupnosť do seba zapadajúcich úsečiek (A_kB_k A_iB_i, i < k ) taká, že pre ľubovoľnú úsečku CD existuje v tejto postupnosti úsečka A_kB_k, ktorá je jej časťou, A_kB_k CD. Potom na priamke p existuje bod M , pre ktorý platí, že je bodom každej úsečky z danej postupnosti.

Ak m je ľubovoľná miera úsečiek a a je ľubovoľné kladné reálne číslo, Cantorova axióma zaručuje existenciu úsečky U, pre ktorú platí m(U) = a.

Pojem dĺžka úsečky AB ( vzdialenosť bodov A, B ) možno definovať po určení jednotky danej miery úsečiek m(U) ako hodnotu tejto funkcie, platí | AB | = m(AB). Vzdialenosť dvoch útvarov je najmenšia zo vzdialeností všetkých dvojíc bodov, z ktorých jeden patrí jednému a druhý druhému útvaru. Podobným spôsobom možno definovať aj veľkosť uhla.

Prvé štyri skupiny axióm tvoria absolútnu geometriu. Doplnením piatej skupiny možno vybudovať euklidovskú alebo neeuklidovskú geometriu, podľa formy jej jedinej axiómy.

V. Axióma rovnobežnosti

V_E: (Euklidova axióma)
Bodom neležiacim na danej priamke prechádza práve jedna priamka rovnobežná s danou priamkou.

V_L: (Lobačevského axióma)
Bodom neležiacim na danej priamke prechádzajú aspoň dve priamky rovnobežné s danou priamkou.

Každá rovina euklidovského priestoru je euklidovskou rovinou, ktorej axiomatická sústava je po vypustení axióm I₄ až I₈ (o vlastnostiach roviny v priestore) zhodná s uvedenou axiomatikou, s akceptovaním Euklidovej axiómy V_E. Zo sústavy axióm, ktoré sa nedajú dokázať pomocou jednoduchších tvrdení, možno vybudovať sústavu tvrdení a viet opisujúcich vlastnosti útvarov priestoru, geometriu priestoru. Mnohé z nich sú predmetom stredoškolského štúdia.