Dagmar Szarková
1. Definície, označenia a ohniskové konštrukcie kužeľosečiek
1.1. Elipsa
Hyperoskulačné kružnice elipsy
1.2. Hyperbola
Ohnisková konštrukcia hyperboly
Hyperoskulačné kružnice hyperboly
1.3. Parabola
Ohnisková konštrukcia paraboly
Hyperoskulačné kružnice paraboly
Úlohy o elipse: {R, 1F, 2F, a} , {s,1F,2F, a}
Úlohy o parabole: {1t, 1T, 2t, 2T} , {M, V, s}
4. Ďalšie vlastnosti a konštrukcie kužeľosečiek
4.1. Elipsa
Zástavková (trojuholníková) konštrukcia elipsy {a,b}
Prúžková konštrukcia elipsy {A, B, M}
Rytzova konštrukcia elipsy {KL, MN}
4.2. Hyperbola
Úlohy o hyperbole {1as, 2as, M}
5.1. Elipsa
5.2. Parabola
5.1. Hyperbola
Koniec stránky – text pre tlač kuzelosečky.doc – Word97
Kužeľosečky sú rovinné krivky druhého stupňa, ktoré delíme na
a) regulárne kužeľosečky: elipsa, parabola hyperbola;
b) singulárne kužeľosečky: bod, priamka, dve priamky.
Všetky typy kužeľosečiek môžeme získať ako rezy kužeľovej plochy rovinou.
a) Ak rezová rovina neprechádza vrcholom, rezom kužeľovej plochy je regulárna kužeľosečka.
b) Ak je rezová rovina vrcholová (prechádza vrcholom), rezom kužeľovej plochy je singulárna kužeľosečka.
V analytickej geometrii ste sa zoznámili s rovnicami kužeľosečiek. Pre zopakovanie si uvedieme definície, dôležité pojmy a ich označovanie. Osvojíme si ohniskové konštrukcie, ktoré vychádzajú z definícií, ako i Ďalšie konštrukcie, ktoré umožňujú narysovať kužeľosečky rýchlejšie ako bodové ohniskové konštrukcie. Uvedieme tiež úlohy, ktoré technik v praxi najčastejšie potrebuje.
Definícia: Elipsa je množina všetkých bodov v rovine E2, ktoré majú od dvoch rôznych bodov 1F, 2F stály súčet vzdialeností rovný 2a, pričom 2a > | 1F 2F |.
(1) Symbolický zápis:
Späť na
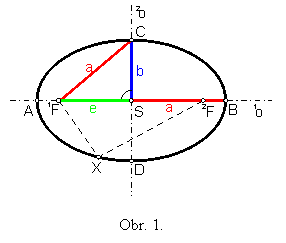
1F, 2F – ohniská
1o – hlavná os (1o = 1F2F)
2o – vedľajšia os (os úsečky 1F2F)
S – stred
A, B – hlavné vrcholy
C, D – vedľajšie vrcholy
a – dĺžka hlavnej polosi a = |AS| = |BS|
b – dĺžka vedľajšej polosi b = |CS| = |DS|
e – excentricita e = |1FS| = |2FS|
D1FSC - charakteristický trojuholník
Dĺžky a, b reprezentujú konštanty v rovnici elipsy
so stredom S(m; n) .
Vzťah medzi dĺžkami a, b vyjadruje Pytagorova veta
a2 = b2 + e2 .
Späť na
Zahradnícka konštrukcia elipsy:
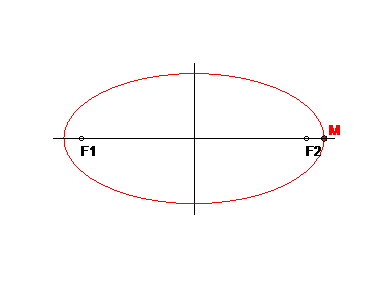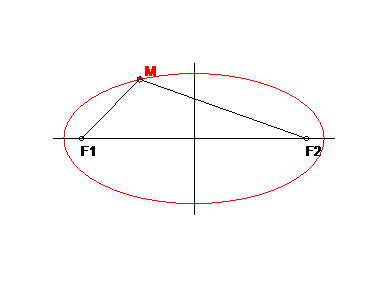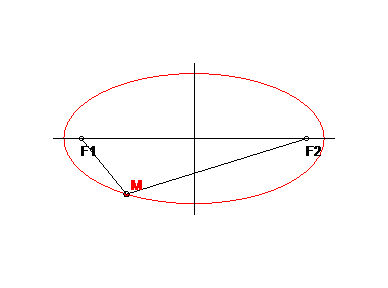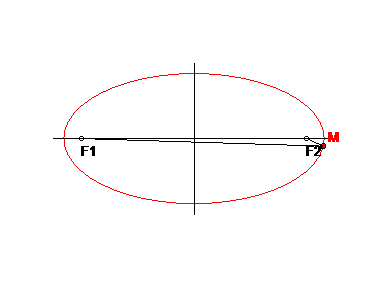
Dané sú ohniská 1F, 2F a úsečka KL dĺžky 2a, 2a > |1F 2F|. Zostrojme elipsu ako množinu bodov s vlastnosťou (1).
Úsečku KL je vhodné umiestniť na os 1o tak, aby sa jej stred stotožnil so stredom úsečky 1F 2F, potom krajné body K, L sa stotožnia s hlavnými vrcholmi A, B elipsy. Bod 1 a ďalšie pomocné body volíme medzi bodmi 1F a S.
Body elipsy získame v prieniku kružníc:
1k ![]() 2k = {1M, 2M},
1k´
2k = {1M, 2M},
1k´ ![]() 2k´= {3M, 4M},
2k´= {3M, 4M},
pričom
1r = |A1| , 2r = |B1| ,
1k(1F; 1r) , 1k´(2F; 1r) ,
2k(2F; 2r) , 2k´(1F; 2r) .
Každý z bodov iM, i=1,...,4 spĺňa vlastnosť:
|iM 1F| + |iM 2F| = 2a ,
je teda bodom elipsy.
Vhodnou voľbou ďalších pomocných bodov a opakovaním konštrukcie získame nové štvorice bodov elipsy.
Z konštrukcie vyplýva, že elipsa je súmerná podľa osí 1o, 2o i podľa stredu S.
Je užitočné osvojiť si konštrukciu kužeľosečiek pomocou hyperoskulačných kružníc, ktorú technici veľmi často používajú.
Hyperoskulačné kružnice nám nahrádzajú oblúky kužeľosečiek v malom okolí ich vrcholov. ( )
Ak skombinujeme ohniskovú konštrukciu kužeľosečky s hyperoskulačnými kružnicami, získame veľmi dobrý základ pre dorysovanie kužeľosečky pomocou krívidla.
Späť na
Úloha č. 1: Zostrojte elipsu, ktorá je daná dĺžkou hlavnej polosi a a dĺžkou vedľajšej polosi b, pomocou hyperoskulačných kružníc.
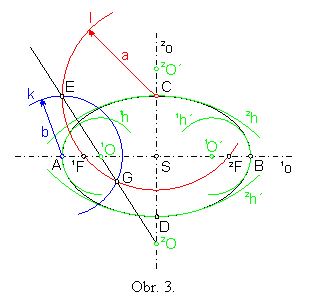
Kružnicové oblúky
1h(1
ktoré sú ich obrazmi v stredovej súmernosti so stredom S, umožnia rýchle narysovanie elipsy pomocou krividla.
Kružnicové oblúky 1h,1h´, sú celé znútra, oblúky 2h, 2h´, sú celé zvonka elipsy.Späť na alebo
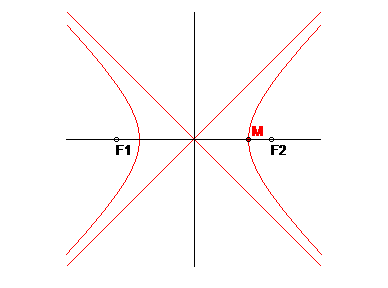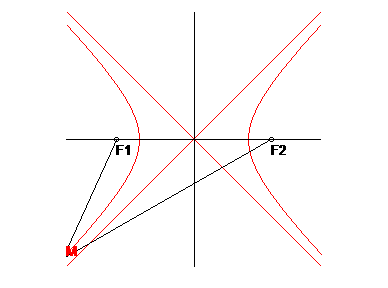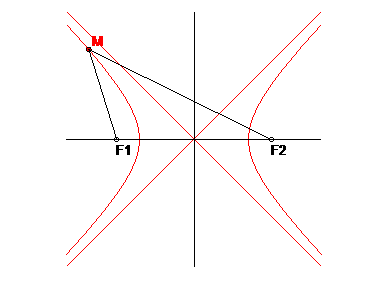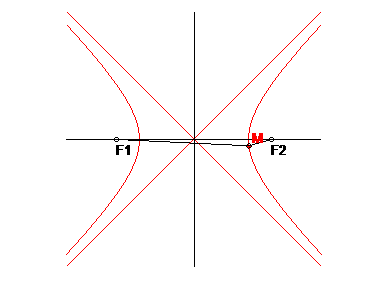
Definícia: Hyperbola je množina všetkých bodov v rovine E2, ktoré majú od dvoch rôznych bodov 1F, 2F stály rozdiel vzdialeností rovný 2a, pričom 0 < 2a < |1F 2F| .
(2) Symbolický
zápis: hyperbola = {X ![]() E
2; | |X1F| – |X2F| | = 2a,
0 < 2a < |1F2F|}
E
2; | |X1F| – |X2F| | = 2a,
0 < 2a < |1F2F|}
Späť na alebo
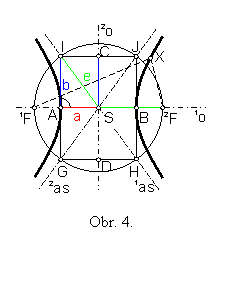
1F, 2F – ohniská
1o – hlavná os (1o = 1F 2F)
2o – vedľajšia os (os úsečky 1F 2F)
S – stred
A, B – hlavné vrcholy
a – dĺžka hlavnej polosi a = |AS| = |BS|
b – dĺžka vedľajšej polosi b = |CS| = |DS|
e = |1FS| = |2FS|
IAS – charakteristický trojuholník
IJGH – charakteristický obdĺžnik
1as, 2as – asymptoty
Body C, D , ktoré ležia na vedľajšej osi, nepatria hyperbole. Sú stredmi protiľahlých strán charakteristického obdĺžnika IJHG, ktorý umožní ľahko zostrojiť asymptoty hyperboly:
1as = IS, 2as = JS.
Rovnica
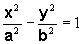
vyjadruje hyperbolu so stredom S(0; 0) a hlavnou osou 1o v x-ovej súradnicovej osi.
Asymptoty uvedenej hyperboly majú rovnice
![]()
Rovnica
vyjadruje hyperbolu so stredom S(m; n) a hlavnou sou 1o rovnobežnou s x-ovou súradnicovou osou.
Z charakteristického trojuholníka IAS hyperboly vyplýva vzťah, ktorý vyjadruje Pytagorova veta: e2= a2+ b2.
Späť na
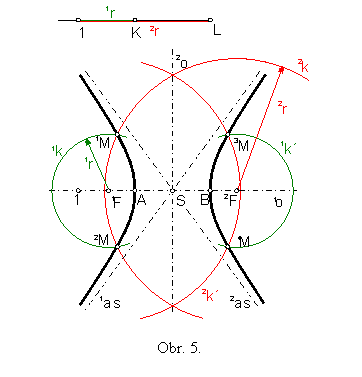
Úsečku KL je vhodné umiestniť na priamku 1o tak, aby sa jej stred stotožnil so stredom úsečky 1F 2F, potom krajné body K, L sa stotožnia s hlavnými vrcholmi A, B hyperboly. Bod 1 a ďalšie pomocné body volíme tak, aby boli vnútornými bodmi na polpriamke opačnej k polpriamke 1FS.
Priesečníky kružníc:
1k ![]() 2k = {1M, 2M}, 1k´
2k = {1M, 2M}, 1k´ ![]() 2k´= {3M, 4M},
2k´= {3M, 4M},
sú bodmi hyperboly, pričom
1r = |A1| , 2r = |B1| ,
1k(1F; 1r) , 1k´(2F; 1r) ,
2k(2F; 2r) , 2k´(1F; 2r) .
Každý z bodov iM, i=1,...,4 spĺňa vlastnosť: | |iM1F| – |iM2F| | = 2a, je teda bodom hyperboly.
Z konštrukcie vyplýva, že hyperbola je súmerná podľa osí 1o, 2o aj podľa stredu S.
Späť na
Bodová konštrukcia hyperboly:
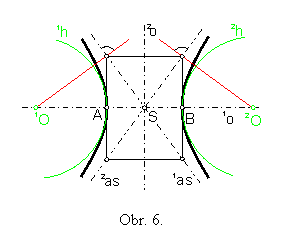
Kolmice na asymptoty prechádzajúce vrcholmi charakteristického obdĺžnika pretínajú
hlavnú os 1o v strede 1O, 2O
Kružnicové oblúky
1h(1
Späť na
Definícia: Parabola
je množina všetkých bodov v rovine E2, ktoré majú rovnaké
vzdialenosti od danej priamky d a od daného bodu F, pričom F ![]() d.
d.
(3) Symbolický
zápis: parabola = {X ![]() E2;
|Xd| = |XF|, F
E2;
|Xd| = |XF|, F ![]() d}
d}
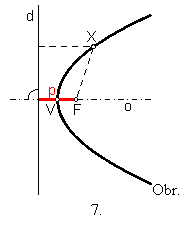
F – ohnisko
d – riadiaca priamka
p – parameter paraboly: p = |Fd|
o – os: F ![]() o
o ![]() o je
kolmá na d
o je
kolmá na d
V – vrchol: V ![]() o
o ![]() |Vd| = |VF|
|Vd| = |VF|
Späť na
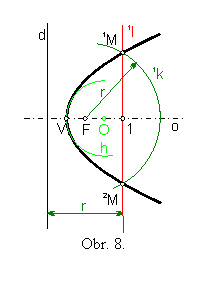
Na polpriamke VF zvoľme bod 1. Body paraboly sú v prieniku pomocnej kružnice
1k(F; |1d|) ,
s priamkou1l prechádzajúcou bodom 1 a rovnobežnou s riadiacou priamkou d
1k ![]() 1l = {1M, 2M} .
1l = {1M, 2M} .
Body 1M, 2M spĺňajú vlastnosť (3) , preto sú bodmi paraboly.
Voľbou ďalších pomocných bodov z polpriamky VF a opakovaním konštrukcie popísanej pre pomocný bod 1 získame ďalšie dvojice bodov paraboly.
Parabola je súmerná podľa osi o, ako vyplýva z konštrukcie jej bodov 1M, 2M
Parabola s osou o rovnobežnou s x-ovou súradnicovou osoua s vrcholom V(m; n) má rovnicu
(y – n)2 = 2p (x – m), ak ohnisko je vpravo od vrchola,
resp. (y – n)2 = –2p (x – m), ak ohnisko je vľavo od vrchola.
Späť na
Hyperoskulačná kružnica
h(O; p = |Fd|) pre
vrchol paraboly má stred O na osi o a polomer rovný dĺžke parametra
p paraboly, leží celá znútra oblúka paraboly.
Späť na
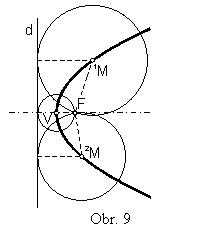
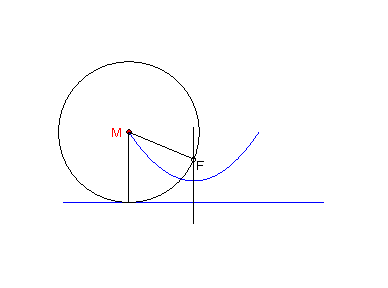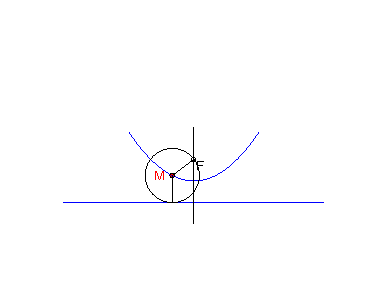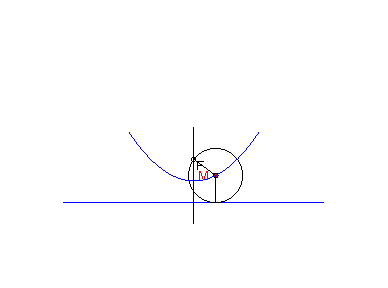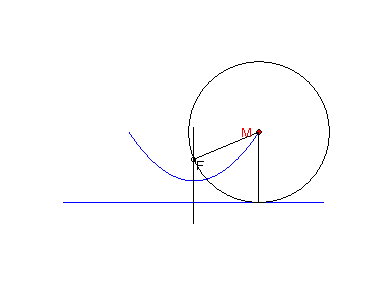
Parabolu s riadiacou priamkou d a ohniskom F možno považovať tiež ako množinu stredov všetkých kružníc, ktoré sa dotýkajú priamky d a prechádzajú bodom F (obr.9).
Späť na
Vnútorné body kužeľosečky sú tie, ktoré ležia spolu s ohniskami v oblasti ohraničenej kužeľosečkou.
Ostatné body roviny, okrem bodov kužeľosečky, sú vonkajšie body kužeľosečky.
Späť na
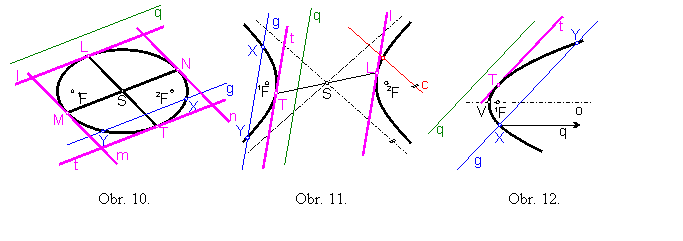
Nesečnica je priamka, ktorá obsahuje iba vonkajšie body kužeľosečky (v obr.10-12 – priamka q).
Sečnica je priamka, ktorá má s kužeľosečkou 2 rôzne spoločné body (v obr.10-12 – priamka g).
Každá priamka, ktorá je rovnobežná s asymptotou hyperboly, má s hyperbolou jeden spoločný bod (v obr.11 – priamka c).
Dotyčnica je priamka t , ktorá má s kužeľosečkou iba jeden spoločný bod T (dotykový bod) a ostatné jej body sú vonkajšie.
Tetiva je úsečka s krajnými bodmi na kužeľosečke, ktorej vnútorné body sú vnútornými bodmi kužeľosečky (v obr.10-12 – úsečka XY).
Priemer stredovej kužeľosečky je úsečka, ktorá prechádza stredom a krajné jej body sú body kužeľosečky (v obr.10-11 – úsečka TL).
Priemer paraboly je polpriamka q rovnobežná s osou o paraboly, je súhlasne orientovaná s polpriamkou VF a začiatok polpriamky je bod paraboly (obr.12).
Združené priemery sú dvojicou priemerov s takou vlastnosťou, že dotyčnice v krajných bodoch jedného priemeru sú rovnobežné s druhým priemerom (obr.10).
Existuje iba jeden pár združených priemerov na seba kolmých a to tie, ktoré ležia na hlavnej a vedľajšej osi – AB je najväčší a CD najmenší zo všetkých priemerov danej elipsy (obr.28).
Späť na
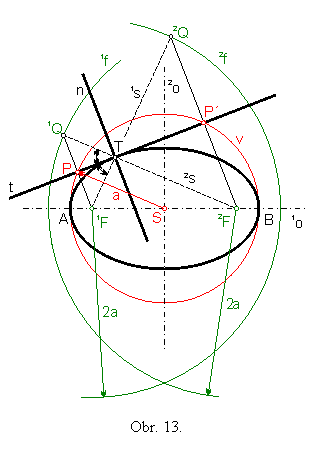
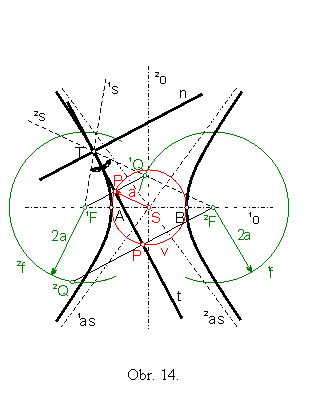
Sprievodiče 1s, 2s sú priamky, ktoré spájajú bod kužeľosečky s jej ohniskami (obr.13-14).
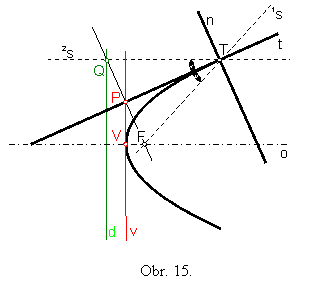
Aby sme vety o dotyčniciach kužeľosečiek mohli formulovať všeobecnejšie, je účelné zaviesť pojem druhého sprievodiča bodu paraboly – budeme ním rozumieť priamku 2s, ktorá prechádza bodom paraboly a je rovnobežná s jej osou (obr.15).
Vonkajším uhlom sprievodičov budeme nazývať uhol, ktorý obsahuje hlavný vrchol.
Vnútorný uhol sprievodičov je susedný k vonkajšiemu uhlu sprievodičov.
V hlavnom vrchole obidva sprievodiče splývajú do jednej priamky. Za vonkajší uhol pokladáme ktorýkoľvek z obidvoch priamych uhlov, ktorých ramená splývajú s hlavnou osou.
Veta 1: Dotyčnica rozpoľuje vonkajší uhol sprievodičov dotykového bodu (obr.13-15).
Veta 2: Normála je kolmica na dotyčnicu v dotykovom bode (rozpoľuje vnútorný uhol sprievodičov dotykového bodu) (obr.13-15).
Veta 3: (o bodoch Q) Množina všetkých bodov Q súmerne združených s jedným ohniskom elipsy (hyperboly) podľa jej dotyčníc je kružnica so stredom v druhom ohnisku a polomerom 2a . (obr.13-14).
Späť na
Bod 1Q je bod súmerne združený s ohniskom
1F podľa dotyčnice t, 1Q ![]() 1f(2F; 2a)
;
1f(2F; 2a)
;
bod 2Q je bod súmerne združený s ohniskom 2F
podľa dotyčnice t, 2Q ![]() 2f(1F; 2a).
2f(1F; 2a).
Kružnice 1f, 2f nazývame riadiacimi kružnicami.
Spojnica bodu iQ (i = 1,2) so stredom riadiacej kružnice, na ktorej leží, pretína dotyčnicu v jej dotykovom bode
Späť na
Veta 4: (o bodoch P)
Množina všetkých piat P kolmíc vedených ohniskom na dotyčnice elipsy
(hyperboly) je kružnica v so stredom S a polomerom rovným dĺžke
hlavnej polosi a, ktorú nazývame vrcholovou kružnicou v(S; a)
(obr.13-14).
Späť na
Veta 3´: (o bodoch Q) Množina všetkých bodov Q súmerne združených s ohniskom paraboly podľa jej dotyčníc je jej riadiaca priamkai d. (obr.15).
Veta 4´: (o bodoch P) Množina všetkých piat P kolmíc vedených ohniskom na dotyčnice paraboly je jej vrcholová dotyčnicaiv (t.j. dotyčnica vo vrchole V) (obr.15).
Späť na
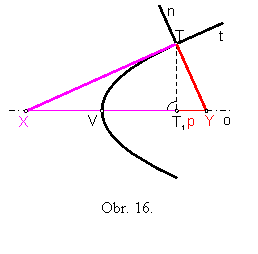
Subtangentou budeme nazývať dĺžku úsečky |XT1|, ktorá je určená priesečníkom X dotyčnice paraboly s jej osou a pätou T1 kolmice vedenej z bodu T na os paraboly (t.j. kolmý priemet bodu T na os paraboly) (obr.16).
Subnormálou budeme nazývať dĺžku úsečky |YT1|, ktorá je určená priesečníkom Y normály paraboly s jej osou a pätou T1 kolmice vedenej z bodu T, ktorým normála prechádza, na os paraboly (obr.16).
Veta 5: Vrchol rozpoľuje subtangentu – |XV| = |VT1| (obr.16).
Veta 6: Dĺžka subnormály sa rovná parametru paraboly p = |T1Y| (obr.16).
Späť na
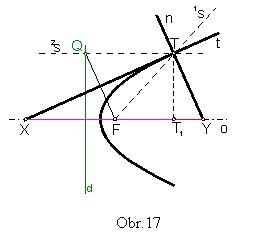
Veta 7: Ohnisko rozpoľuje úsečku, ktorá je súčtom subtangenty
a subnormály. |QT| = |XF| = |FY| (obr.17)
Späť na
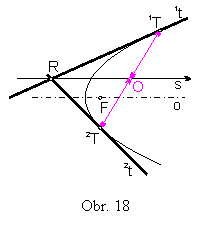
Veta 8: Spojnica priesečníka dvoch rôznych dotyčníc 1t,
2t paraboly so stredom tetivy určenej ich dotykovými bodmi
1T, 2T je rovnobežná s osou paraboly.
(obr.18)
Späť na alebo
V praxi sa veľmi často stretávame s úlohou narysovať dotyčnice z bodu k elipse (napr.obrysové tvoriace priamky kužeľovej plochy), resp. narysovať dotyčnice rovnobežné s daným smerom (napr. obrysové tvoriace priamky valcovej plochy).
Úloha č. 2: Zostrojte dotyčnice k elipse z jej vonkajšieho bodu R . Elipsa je daná ohniskami 1F, 2F a dĺžkou hlavnej polosi a. (obr.19)
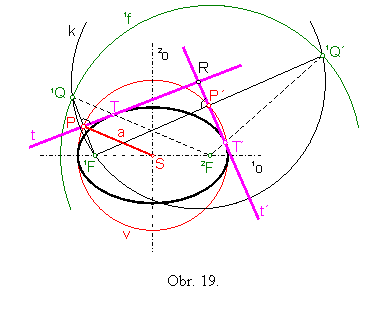
Podľa vety 3 (o bodoch Q) bod 1Q musí ležať na riadiacej kružnici 1f(2F; 2a).
Riešenie: Body 1Q a 1Q´ nájdeme v prieniku kružníc k a 1f.
Dotyčnice t a t´ prechádzajú bodom R a sú osami úsečkiek 1F1Q a 1F1Q´.Dotykové body T a T´ získame v prieniku dotyčnice t resp. t´ so spojnicou bodu 1Q resp. 1Q´ so stredom 2F riadiacej kružnice 1f.
Úloha č. 3: Zostrojte dotyčnice k elipse rovnobežné s daným smerom s. Elipsa je daná ohniskami 1F,2F a dĺžkou hlavnej polosi a. (obr.20)
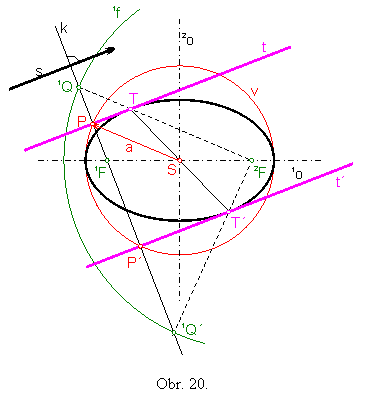
Poznámka: Úlohy o konštrukcii dotyčníc zostrojených z daného vonkajšieho bodu R alebo dotyčníc rovnobežných s daným smerom s k hyperbole (parabole) sa riešia analogicky ako úloha č.2 alebo úloha č.3. Pre parabolu namiesto vety 3 a 4 využijeme vetu 3´ a 4´.
Veľmi často stojíme pred úlohou zostrojiť parabolu, ktorá je daná dvoma dotyčnicami s ich dotykovými bodmi.
Úloha č. 4: Zostrojte parabolu, ak poznáte dotyčnice 1t, 2t s dotykovými bodmi 1T, 2T.
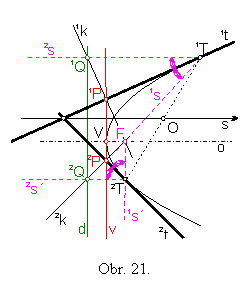
Riešenie:
Pre vyhľadanie smeru osi s paraboly použijeme vetu 8 (obr.21).
V bodoch 1T a 2T zostrojíme sprievodiče 2s, 2s´, ktoré sú rovnobežné s vyhľadaným smerom osi s paraboly.
Podľa vety 1 vieme zostrojiť sprievodiče 1s, 1s´ v týchto bodoch.
Sprievodiče 1s, 1s´ sa pretnú v ohnisku F, ktorým prechádza os o. Os o je rovnobežná s vyhľadaným smerom s.
Úlohu č.4 môžeme riešiť aj pomocou lichobežníkovej metódy, pomocou ktorej vyhľadáme vrchol paraboly (obr.22).
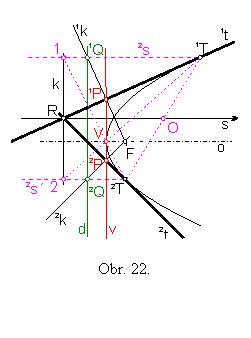
Kolmica k v bode R (R=1t ![]() 2t)
na smer s, ktorý je vyhľadaný podľa vety 8, pretne sprievodiče
2s, 2s´ v bodoch 1 a 2.
Takto získame lichobežník 11T2T2, ktorého uhlopriečky
sa pretnú vo vrchole V hľadanej paraboly.
2t)
na smer s, ktorý je vyhľadaný podľa vety 8, pretne sprievodiče
2s, 2s´ v bodoch 1 a 2.
Takto získame lichobežník 11T2T2, ktorého uhlopriečky
sa pretnú vo vrchole V hľadanej paraboly.
Os o prechádza vrcholom V rovnobežne s vyhľadaným smerom s.
Podľa vety 4´ päty 1P a 2P kolmíc 1k a 2k zostrojených z ohniska F na dotyčnice ležia na vrcholovej dotyčnici v, preto vrcholovúdotyčnicu v vieme zostrojiť. Ohnisko F je v priesečníku kolmíc 1k, 2k . Pri konštrukcii stačí hľadať ohnisko F ako priesečník jednej kolmice, napr. 1k, s osou o.
Riadiacu priamku d, ktorá je kolmá na os paraboly nájdeme pomocou ohniskovej vlastnosti paraboly (|Vd| = |VF|) resp. pomocou vety 3´ body 1Q a 2Q, pre ktoré platí: |1Q 1P| = |1P F| , |2Q 2P|=|2P F|, ležia na riadiacej priamke d).
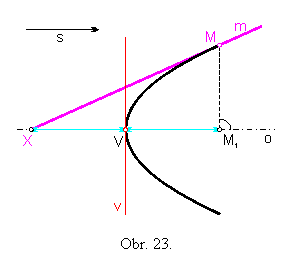
Úloha č. 5: Zostrojte dotyčnicu paraboly v jej danom bode M, ak poznáte vrchol V a smer s osi paraboly. (obr.23)
Riešenie:
Na osi o, ktorá prechádza bodom V a je rovnobežná s daným
smerom s, nájdeme kolmý priemet M1 dotykového bodu
M.
Podľa vety 5 (o subtangente) vieme zostrojiť priesečník X osi o a hľadanej dotyčnice ako obraz bodu M1 v stredovej súmernosti podľa bodu V.
Priamka MX je hľadaná dotyčnica m paraboly v danom
bode M.
Úloha č. 6: Zostrojte vrchol V, ohnisko F a riadiacu priamku d už narysovanej paraboly.
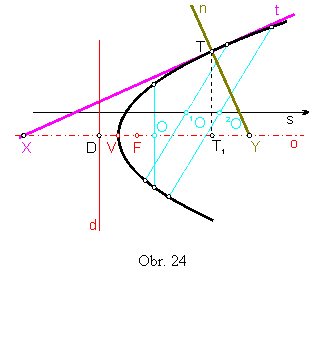
Riešenie: (obr.24)
Zostrojíme dve rovnobežné tetivy, ktorých spojnica stredov 1O,
2O určí smer s osi o paraboly.
Os o bude prechádzať stredom O tetivy kolmej na smer osi a bude rovnobežná s vyhľadaným smerom s. Os o pretne parabolu v jej vrchole V.
Zostrojíme pätu T1 kolmice z ľubovoľného bodu T paraboly na os o. Bod X, ktorý je obrazom bodu T1 v stredovej súmernosti podľa vrchola V nám umožní zostrojiť dotyčnicu t = XT – podľa vety 5 (o subtangente).
Normála n v bode T pretne os o v bode Y. Podľa vety 7 je ohnisko F stredom úsečky XY. Pre zostrojenie riadiacej priamky d použijeme vetu 6 (o subnormále) - |T1Y| = p, teda p = |Fd| = |DF|.
Späť na
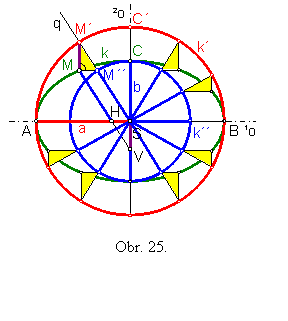
Ak je elipsa daná polohou osí 1o, 2o a dĺžkami polosí a, b, môžeme pre konštrukciu jej bodov využiť zástavkovú (trojuholníkovú) konštrukciu, ktorá využíva dvojakú afinitu medzi:
1) elipsou k a kružnicou k´(S;a) so smerom afinity 2o
2) elipsou k a kružnicou k´´(S;b) so smerom afinity 1o
Veďme ľubovoľnú polpriamku q so začiatkom S v strede elipsy a označme M´ jej priesečník s kružnicou k´ a M´´ s kružnicou k´´. Spojnica bodov MM´ musí byť rovnobežná so smerom 2o prvej afinity, a súčasne MM´´ musí byť rovnobežná so smerom 1o druhej afinity. Zostrojený bod M elipsy je preto vrcholom pravouhlého trojuholníka s preponou M´M´´.
Popísaným spôsobom môžeme zostrojiť ľubovoľný počet bodov elipsy.
Poznámka č. 1: Vo vrcholoch elipsy sa pravouhlé trojuholníky degenerujú do úsečiek.
Poznámka č. 2: Z rovnobežníka SM´MV vyplýva |MV| = |M´S| = a a z rovnobežníka SM´´MH vyplýva |MH| = |M´´S| = b, ako je vidieť z obr. 25.
Uvedené vzťahy sú zdôvodnením nasledujúcej rozdielovej prúžkovej konštrukcie.
Späť na
Ak je elipsa daná polohou osí 1o, 2o a dĺžkami polosí a, b, môžeme pre konštrukciu bodov elipsy využiť tiež rozdielovú alebo súčtovú konštrukciu:
Na prúžok papiera si vyznačíme bod M, od ktorého nanesieme dĺžku a (a = |MV|, alebo a = |MV´|) a dĺžku b (b = |MH|, alebo b = |MH´|), čím získame bod V (alebo V´) a bod H (alebo H´).
Umiestnime prúžok papiera tak, aby bod V bol na vedľajšej osi 2o a súčasne bod H na hlavnej osi 1o; v mieste bodu M môžeme vyznačiť bod danej elipsy.
Pohybom prúžka papiera tak, že H ![]() 1o
a súčasne V
1o
a súčasne V ![]() 2o,
s následným vyznačením bodu M, získame body elipsy.
2o,
s následným vyznačením bodu M, získame body elipsy.
Uvedené konštrukcie bodov elipsy sú princípom mechanického zariadenia na kinematické vytvorenie (rysovanie) elipsy, tzv. elipsografu.
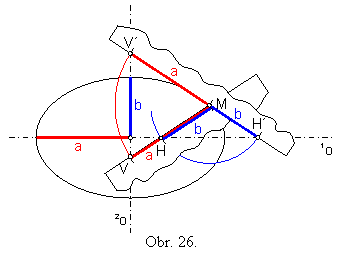
Úloha č. 7: Zostrojte elipsu, ktorá je daná hlavnými vrcholmi A, B a bodom M elipsy.
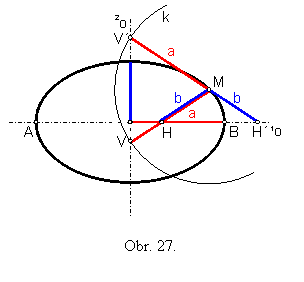
Riešenie: (obr.27)
Pri hľadaní dĺžky vedľajšej polosi využijeme prúžkovú konštrukciu.
Kružnica k(M; a) pretne vedľajšiu os 2o v bodoch V a V´.
Ak spojíme bod M elipsy s bodom V, získame dĺžku vedľajšiej polosi b na základe rozdielovej prúžkovej konštrukcie.
Spojnica MV´ súvisí s konštrukciou dĺžky vedľajšej polosi b pomocou súčtovej prúžkovej konštrukcie.
Ak poznáme hlavné vrcholy elipsy a dĺžku b, môžeme pre narysovanie elipsy použiť ľubovoľnú z predchádzajúcich konštrukcií.
Späť na
V praxi sa často stretávame s úlohou zostrojiť elipsu, ktorá je daná združenými priemermi. Vzhľadom na vlastnosti združených priemerov ide v skutočnosti o úlohu vpísať elipsu do dotyčnicového rovnobežníka. Hoci zručný technik naškicuje elipsu bez väčších problémov, musí vedieť elipsu narysovať presne. Najvhodnejšií spôsob je osvojiť si Rytzovu konštrukciu (úloha č.8 – obr.28).
Úloha č. 8: Zostrojte elipsu, ktorá je daná združenými priemermi KL, MN
Nad jedným priemerom, napr. KL opíšeme polkružnicu k(S; |SK|).
Bodom S zostrojíme kolmicu q, ktorá pretne kružnicu k v bode G.
Nájdeme stred O úsečky GM (M je bližší z koncových bodov druhého priemeru).
Kružnica l(O; |OS|) pretne priamku GM v bode H a V.
Dĺžka hlavnej polosi a = |VM| = |GH
Hlavná os elipsy 1o = HS leží v ostrom uhle daných združených priemerov.
2o = VS je vedľajšía os elipsy.
Späť na alebo
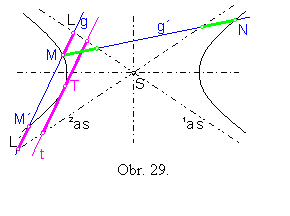
Veta 9: Dĺžky úsečiek na priamke medzi bodmi hyperboly a priesečníkmi
s asymptotami sú rovnaké: |ML| = |M´L´| (obr.29).
Späť na alebo
Dôsledok: Dotykový bod T dotyčnice t rozpoľuje úsečku tejto dotyčnice ohraničenú asymptotami (obr.29).
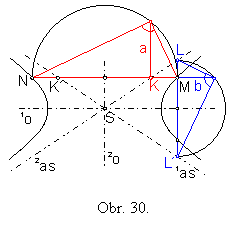
Veta 10: Súčin úsečiek na priamke rovnobežnej s hlavnou osou hyperboly od bodu jednej asymptoty po priesečníky tejto priamky s hyperbolou sa rovná obsahu štvorca nad dĺžkou hlavnej polosi, t.j. |MK| . |KN| = a2. (obr.30)
Veta 11: Súčin úsečiek na priamke rovnobežnej s vedľajšou osou hyperboly od bodu hyperboly po priesečníky tejto priamky s asymptotami sa rovná obsahu štvorca nad dĺžkou vedľajšej polosi, t.j. |ML| . |ML´ |= b2. (obr.30)
Späť na alebo
Z týchto viet vyplýva jednoduchá konštrukcia hyperboly, ktorá je daná asymptotami a bodom hyperboly (úloha č.9), ktorú veľmi často potrebujeme pri riešení úloh rezov na kužeľovej ploche a hyperboloide.
Úloha č. 9: Narysujte hyperbolu, ak poznáte asymtoty 1as, 2as a bod M, ktorý leží na hyperbole
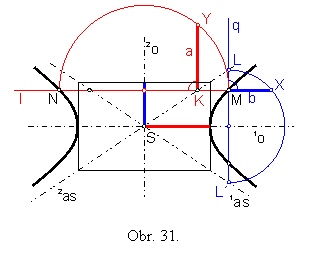
Riešenie: (obr.31)
Pri riešení použijeme buď vetu 10, alebo vetu 11.
Zostrojíme hlavnú os 1o ako os toho uhla asymptôt, v ktorom leží bod M hľadanej hyperboly. Vedľajšia os 2o je na hlavnú os 1o kolmá a prechádza stredom S = 1as 2as hyperboly.
Ak použijeme vetu 10, zostrojíme bodom M priamku l, ktorá je rovnobežná s hlavnou osou 1o a vyznačíme na nej bod N hyperboly (podľa vety 9).
Zostrojíme Talesovu kružnicu nad úsečkou MN. Kolmica zostrojená v bode K pretne Talesovu kružnicu vo vrchole Y pravouhlého trojuholníka NYM. Z Euklidovej vety o výške trojuholníka získame vzťah |M K | . | K N| = a2, teda výška pravouhlého trojuhoníka NYM bude dĺžkou hlavnej polosi a. Pomocou charakteristického obdĺžnika ľahko zostrojíme dĺžku vedľajšej polosi b.
Ak použijeme vetu 11, zostrojíme bodom M priamku q, ktorá je rovnobežná s vedľajšou osou 2o a priesečníky priamky q s asymptotami označíme L, L´.
Nad úsečkou LL´ zostrojíme Talesovu kružnicu, ktorá pretne priamku l v bode X. Z Euklidovej vety o výške trojuholníka získame vzťah |ML| . |ML´| = b2, teda výška pravouhlého trojuhoníka LXL´ bude dĺžkou vedlajšej polosi b. Dĺžku a hlavnej polosi zostrojíme pomocou charakteristického obdĺžnika.
Späť na
Pre ucelenejší pohľad na kužeľosečky je vhodné sa s nimi oboznámiť pomocou ich modelovania. Každú jednu kužeľosečku môžete modelovať pomocou zmeny hodnôt parametrov všeobecnej rovnice.
Tuto stránku si môžete nahrať ako doc-súbor, ktorý je v komprimovanom tvare:
Späť na
Posledná zmena: 27. novembra 2008