|
Measures of Spread
Target: On completion of this worksheet you should understand what is meant by a measure of spread and be able to calculate range, interquartile range and standard deviation.
Suppose there are two football teams, A and B, and we need to choose one of them to take part in a competition. In this competition consistency is important. In order to make our decision we will use the number of goals they scored in their last 11 matches.
| A | 4 | 7 | 0 | 1 | 2 | 0 | 6 | 7 | 4 | 2 | 0 |
| B | 3 | 3 | 2 | 3 | 3 | 3 | 2 | 4 | 4 | 3 | 3 |
We will first consider the mean number of goals for each team:
mean A = ![]() mean B =
mean B = ![]()
The means are equal so we must use other criteria. As consistency is important we need to find some way of measuring the spread of the data.
The range of a set of data = largest value – smallest value
Using our football data:
range A = 7 – 0 = 7
range B = 4 – 2 = 2
As team B has a lower range than team A we would choose team B for consistency.
In general although the range is very easy to find it can be distorted by one very high or very low figure particularly if there is a large amount of data.
The median divides the data into two halves (see Averages worksheet). The quartiles with the median divide the data into quarters.
To find the median and quartiles the data must first be put in numerical order
Team A: 0 0 0 1 2 2 4 4 6 7 7
The median is the 6th value (shown in red), the lower quartile (Q1) is the 3rd value (shown in blue) and the upper quartile (Q3) is the 9th value (shown in green).
0 0 0 1 2 2 4 4 6 7 7![]()
![]()
We can see that these values divide the data into four equal parts. Now another measure of spread is the interquartile range = Q3 – Q1
Interquartile range for A = 6 – 0 = 6
For team B we must first arrange the data in order as before:
2 2 3 3 3 3 3 3 3 4 4![]()
![]()
The quartiles and median are in the same positions as for team A.
Interquartile range for B = 3 – 3 = 0
The standard deviation uses all the values and gives a more useful measure of spread. The formula is
standard deviation (usually abbreviated to s.d.) = 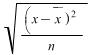
where ![]() is the mean value of the data.
is the mean value of the data.
Using the football teams data (mean = 3)
| A | B | ||||
|
|
|
|
|
|
|
| 4 | 1 | 1 | 3 | 0 | 0 |
| 7 | 4 | 16 | 3 | 0 | 0 |
| 0 | -3 | 9 | 2 | -1 | 1 |
| 1 | -2 | 4 | 3 | 0 | 0 |
| 2 | -1 | 1 | 3 | 0 | 0 |
| 0 | -3 | 9 | 3 | 0 | 0 |
| 6 | 3 | 9 | 2 | -1 | 1 |
| 7 | 4 | 16 | 4 | 1 | 1 |
| 4 | 1 | 1 | 4 | 1 | 1 |
| 2 | -1 | 1 | 3 | 0 | 0 |
| 0 | -3 | 9 | 3 | 0 | 0 |
|
|
|
|
|
||
Standard deviation of A = ![]()
Standard deviation of B = ![]()
Note the use of the Greek letter ![]() for s.d.
for s.d.
The formula can also be written 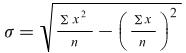
For a frequency distribution the formula is 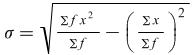
This formula is also used for a grouped frequency distribution where x is the mid-point of the interval.
You can use your calculator to work out the mean and standard deviation. First put your calculator into statistics mode and then clear all memories. Each x value is entered ( multiplied by frequency if needed ) followed by ‘DATA’ key. How to display the mean and standard deviation depends on your calculator.
Find the standard deviation of the following data:
| Goals scored | Number of matches | ||
|
|
|
|
|
| 0 | 10 | 0 | 0 |
| 1 | 29 | 29 | 29 |
| 2 | 32 | 64 | 128 |
| 3 | 23 | 69 | 207 |
| 4 | 6 | 24 | 96 |
|
|
|
|
![]()
This is the standard deviation for the population of 100 matches, i.e. for the data given. If we want to use this data as a sample to estimate the standard deviation for the population of all matches then we must use a slightly different formula which gives a better estimate. We use s to denote this standard deviation.
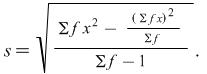 Applying this to the example above gives us the result
Applying this to the example above gives us the result

As the number of values is large there is little difference between the two standard deviations but this second formula should be used when estimating a population standard deviation.
The variance is the square of the standard deviation so