|
The Poisson Distribution
If a random event occurs with known average over a fixed interval (this may be time, distance, area or volume), the Poisson Distribution can be used to calculate the probability of a number of these random events occuring over an interval. If the number of these events is ![]() , the discrete probability distribution is given by
, the discrete probability distribution is given by
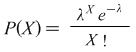
![]()
where ![]()
![]() is the exponential constant and
is the exponential constant and ![]() is the mean value of the distribution.
is the mean value of the distribution.
i) A bus service runs from a bus stop on average every 12 minutes. What is the probability of 3 buses arriving over a period of 24 minutes?
Solution:
The average number of buses over a 24 minute period is ![]() buses. The probability of 3 buses arriving during a 24 minute interval is therefore given by
buses. The probability of 3 buses arriving during a 24 minute interval is therefore given by
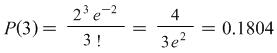 .
.
ii) Another bus service runs on average every 6 minutes. What is the probability of 2 or more buses arriving at the stop in a 9 minute period?
Solution:
The probability of 2 or more buses arriving is ![]() .
.
The average number of buses over a 9 minute period is ![]() buses.
buses.
The probability of 0 buses arriving at the stop over a 9 minute period is given by
![]() .
.
The probability of 1 bus arriving at the stop over a 9 minute period is given by
![]() .
.
The probability of 2 or more buses arriving is therefore ![]() .
.
The mean of a Poisson distribution is given by ![]() .
.
The variance of a Poisson distribution is given by ![]() .
.
The standard deviation of a Poisson distribution is given by ![]() .
.
The moment generating function of the Poisson dsitribution is given by
![]() .
.