

|
Fractions or rational numbers
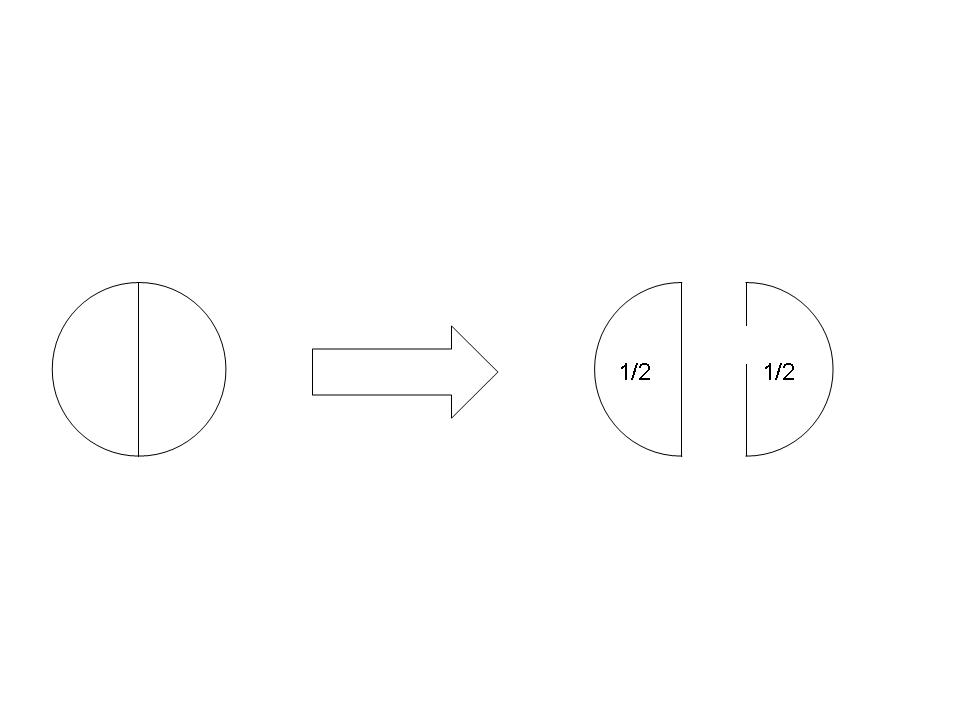
A fraction (also called rational number, vulgar fraction or common fraction) is a way of expressing a number of equal parts of a whole. It is composed of a numerator and a denominator. The denominator is a number which represents the whole, whilst the numerator represents the number of parts of the whole. For example, if we take a circle and divide it into two equal slices, each of the slices is half of the whole, written as ![]() or
or ![]() (see diagram below). It will be noted that the denominator is always written on the bottom of the fraction.
(see diagram below). It will be noted that the denominator is always written on the bottom of the fraction.
|
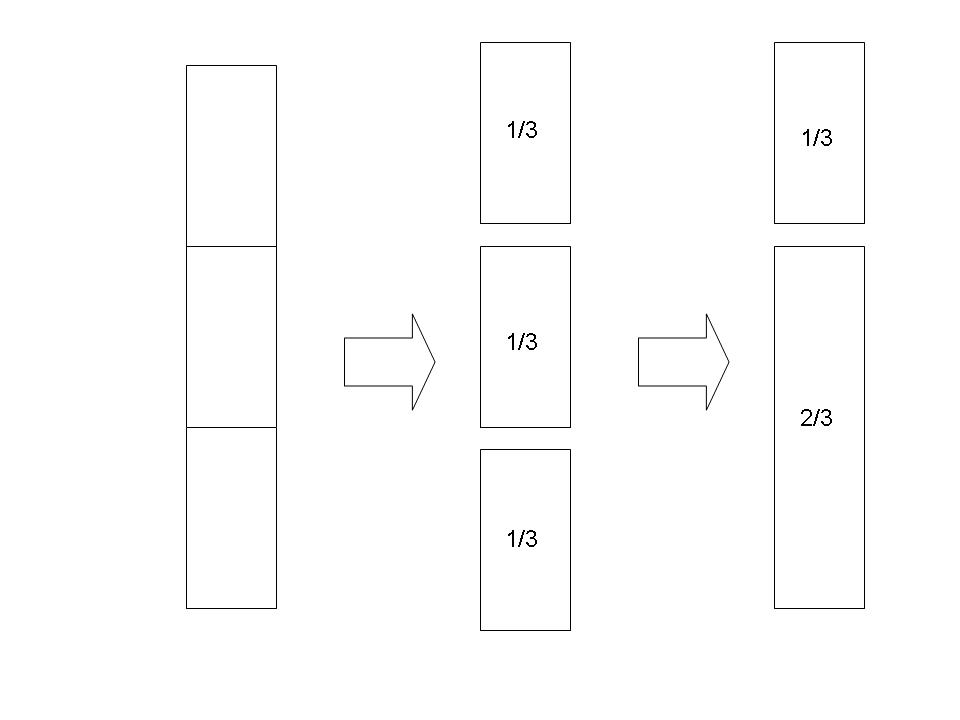
Similarly, if we take a rectangle and divide it into 3 equal pieces, then each of the pieces is one third of the whole, written as ![]() (or
(or ![]() ). If only one piece is removed, the remaining piece represents two thirds, written as
). If only one piece is removed, the remaining piece represents two thirds, written as ![]() (see diagram below).
(see diagram below).
|
If the numerator is smaller in size than the denominator the fraction is called a proper fraction. Examples of proper fractions are ![]() . If the numerator is greater in size than the denominator, the fraction is called an improper or top-heavy fraction. Examples of improper fractions are
. If the numerator is greater in size than the denominator, the fraction is called an improper or top-heavy fraction. Examples of improper fractions are ![]() .
.
An improper fraction can also be written as a mixed number by converting it into a combination of an integer and a proper fraction. This is achieved by dividing the numerator by the denominator and using the remainder to create the numerator for the required proper fraction.
i) Convert ![]() to a mixed number.
to a mixed number.
Solution:
Divide 4 by 3, giving the answer 1 remainder 1. This is usually written as ![]() . The required mixed number is therefore
. The required mixed number is therefore ![]() .
.
ii) Convert ![]() to a mixed number.
to a mixed number.
Solution:
![]() . The required mixed number is therefore
. The required mixed number is therefore ![]() .
.
Two fractions are equivalent when the ratio of the numerator to the denominator is the same for both of them. A simple example is given by comparing ![]() and
and ![]() . The numerator and denominator of are both twice the value of the numerator and denominator of . The ratio is therefore the same i.e. 1:2, and the fractions are consequently equivalent. Another way of looking at this is to take any fraction and repeatedly multiply top and bottom by the same number (called a common factor) to give a sequence of equivalent fractions e.g.
. The numerator and denominator of are both twice the value of the numerator and denominator of . The ratio is therefore the same i.e. 1:2, and the fractions are consequently equivalent. Another way of looking at this is to take any fraction and repeatedly multiply top and bottom by the same number (called a common factor) to give a sequence of equivalent fractions e.g. ![]() . Since multiplying top and bottom by the same number always preserves the ratio, there are an infinite number of equivalent fractions.
. Since multiplying top and bottom by the same number always preserves the ratio, there are an infinite number of equivalent fractions.
Find an equivalent fraction for ![]() .
.
Solution:
Take any number and multiply both numerator and denominator by that number. In this case, for example, take 5. Then ![]() .
.
![]() is therefore an equivalent fraction for
is therefore an equivalent fraction for ![]() .
.
When a fraction is in a form where it cannot be further divided in numerator and denominator, it is said to be in its lowest terms or in the form of a simplest fraction.
Write ![]() in its lowest terms.
in its lowest terms.
Solution:
22 and 77 have a common factor of 11, which divides into 22 twice and into 77 seven times.
We can therefore write ![]() as
as ![]() . This process is called cancelling. The only number which divides into both 2 and 7 is 1. The fraction
. This process is called cancelling. The only number which divides into both 2 and 7 is 1. The fraction ![]() is therefore in its lowest terms.
is therefore in its lowest terms.
In some cases, if it is not obvious which is the highest number which divides numerator and denominator, it may be necessary to divide more than once.
Write ![]() in its lowest terms.
in its lowest terms.
Solution:
Clearly, both 160 and 240 are divisible by 10, as they both end in a 0. We can initially reduce the fraction thus:
![]() . Both 16 and 24 are divisible by 8, giving a further reduction
. Both 16 and 24 are divisible by 8, giving a further reduction
![]() . 2 and 3 are only divisible by 1. The fraction
. 2 and 3 are only divisible by 1. The fraction ![]() is therefore in its lowest terms.
is therefore in its lowest terms.