

|
Complex Numbers
A complex number, ![]() , is a combination of a real number and an imaginary number, and is written in the form
, is a combination of a real number and an imaginary number, and is written in the form ![]() or
or ![]() .
. ![]() is called the real part of
is called the real part of ![]() and
and ![]() is called the imaginary part of
is called the imaginary part of ![]() If
If ![]() ,
, ![]() is called a pure imaginary number and if
is called a pure imaginary number and if ![]() ,
, ![]() is called a pure real number. Two complex numbers are equal if and only if both their real and imaginary parts are equal i.e. if
is called a pure real number. Two complex numbers are equal if and only if both their real and imaginary parts are equal i.e. if ![]() ,
, ![]() and
and ![]() then
then ![]() and
and ![]() .
.
|
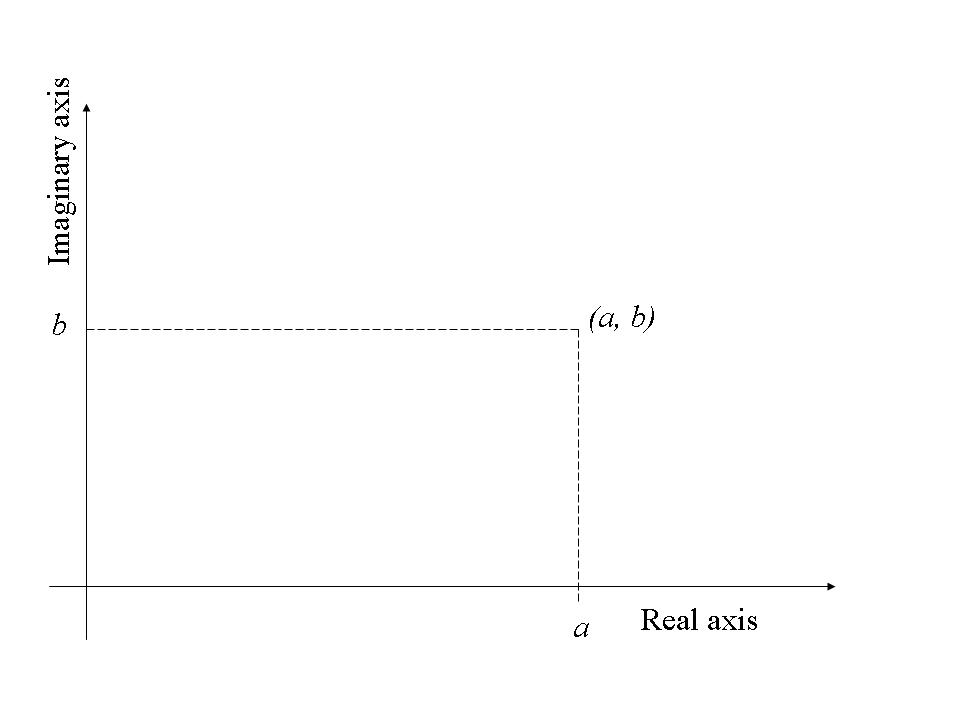
The easiest way to geometrically represent a complex number is by using an Argand Diagram (see above). The point ![]() represents the complex number
represents the complex number ![]() . All pure real numbers exist on the real axis and all pure imaginary numbers exist on the imaginary axis. The set of all points representing all complex numbers is called the complex plane.
. All pure real numbers exist on the real axis and all pure imaginary numbers exist on the imaginary axis. The set of all points representing all complex numbers is called the complex plane.
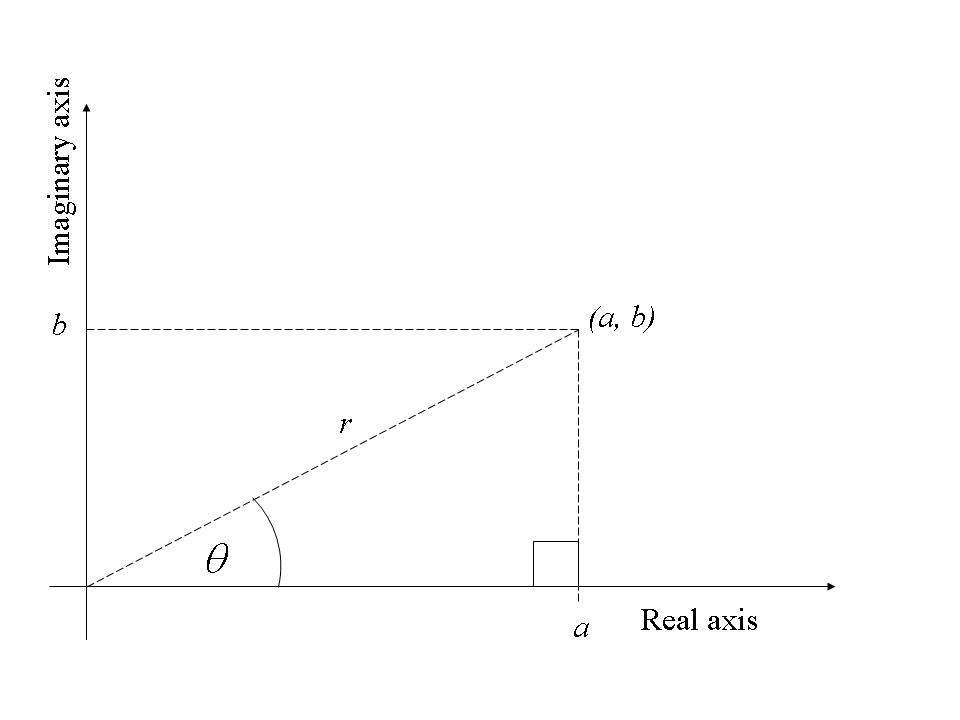
As an alternative to using Cartesian co-ordinates, it is possible to specify the point ![]() by the length of the line connecting the origin with the point and the angle this line makes with the positive real axis (see diagram below).
by the length of the line connecting the origin with the point and the angle this line makes with the positive real axis (see diagram below).
|
The length, ![]() , is called the modulus of
, is called the modulus of ![]() and is denoted either by
and is denoted either by ![]() or
or ![]() The angle,
The angle, ![]() , is called the argument of
, is called the argument of ![]() , denoted by
, denoted by ![]() . Since
. Since ![]() all represent the same point, it is conventional to restrict the range of the argument to
all represent the same point, it is conventional to restrict the range of the argument to ![]()
![]() . This is called the principal value of the argument. It will be noted that, by pythagoras’ theorem,
. This is called the principal value of the argument. It will be noted that, by pythagoras’ theorem, ![]() , so that
, so that ![]() .
.
Also, ![]() , so that
, so that ![]() . Care must be taken when calculating the argument. For example, if the point is in the third quadrant, so that both
. Care must be taken when calculating the argument. For example, if the point is in the third quadrant, so that both ![]() and
and ![]() are negative,
are negative, ![]() gives the value of the angle in the first quadrant, whereas the true value is
gives the value of the angle in the first quadrant, whereas the true value is ![]() .
.
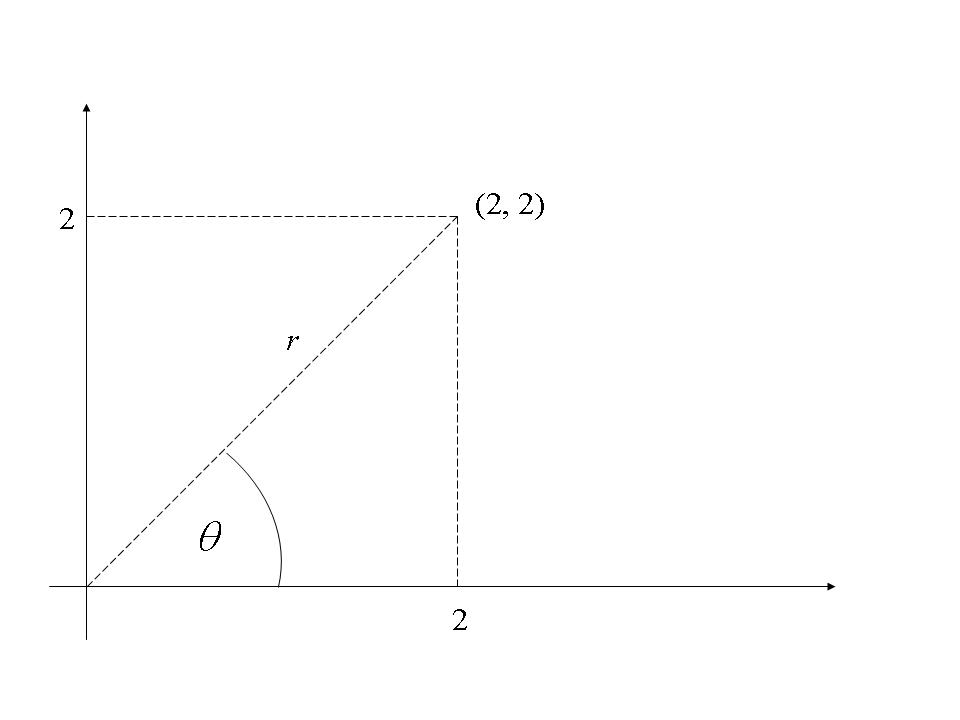
Determine the modulus and argument of ![]() where
where ![]()
i)![]()
![]()
ii)![]()
![]()
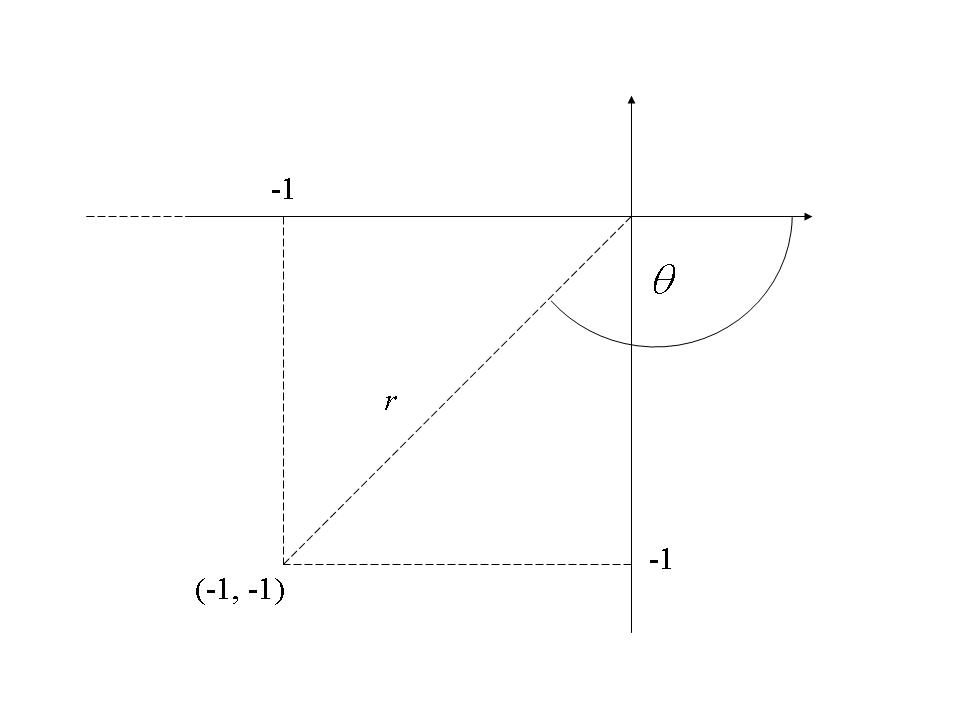
iii) ![]()
Solutions:
i) It is generally a good idea to sketch an Argand diagram for each case.
|
![]() .
.
![]() .
.
ii)

|
![]() .
.
![]() .
.
iii)
|
![]() .
.
Look at the Argand diagram - the point is in the 3rd quadrant.
![]() - the argument of
- the argument of ![]() is therefore given by
is therefore given by
![]() .
.
Using elementary trigonometry it can be seen that ![]() and
and ![]() .
.
Any complex number can therefore be written in the alternative form
![]() .
.
This is called the polar form of the complex number (as distinct from the cartesian form shown above), and is frequently abbreviated by either ![]() or
or ![]() .
.
Express the following complex numbers in polar form:
i)![]()
![]()
ii)![]()
![]()
iii) ![]()
Solutions:
The modulus and argument for these numbers have already been calculated in 4.2.1 above.
i) ![]() .
.
![]() is therefore written in polar form as
is therefore written in polar form as ![]() .
.
ii) ![]() .
.
![]() is therefore written in polar form as
is therefore written in polar form as ![]() .
.
iii) ![]() .
.
![]() is therefore written in polar form as
is therefore written in polar form as ![]() .
.
Note that although ![]() is negative, we have converted it to a positive value in the polar representation.
is negative, we have converted it to a positive value in the polar representation.
Whilst conversion from cartesian to polar form is straightforward, conversion from polar to cartesian form can be a little more tricky. As always, it is a good idea to sketch an Argand diagram.
Express the following complex numbers in cartesian form:
i) ![]()
ii)![]()
iii) ![]()
Solutions:
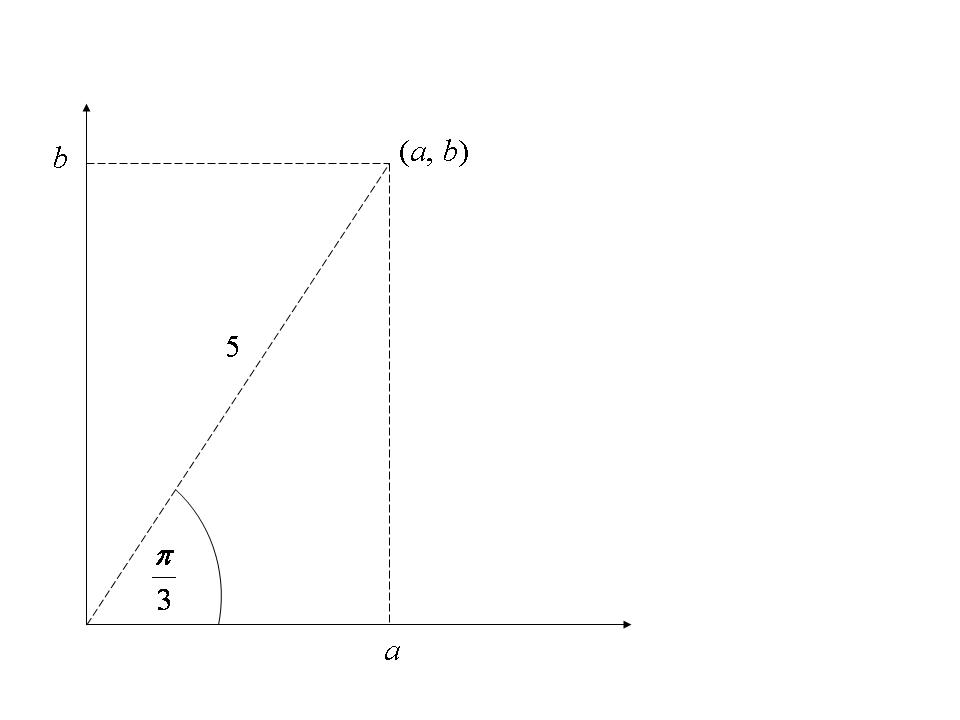
i) Both the cosine and the sine terms are positive, and ![]() , so the point is in the first quadrant.
, so the point is in the first quadrant.
|
The value of ![]() is given by
is given by ![]() and the value of
and the value of ![]() is given by
is given by 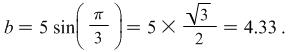
Therefore, in cartesian form, ![]() .
.
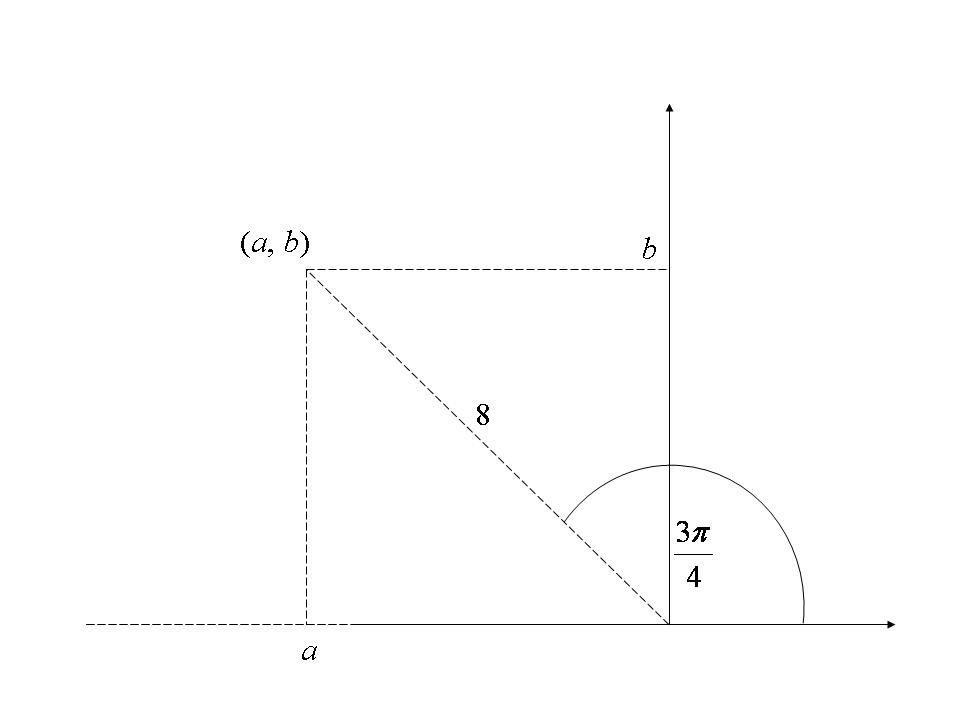
ii) Both the sine and cosine terms are positive, and ![]() , so the point is in the second quadrant.
, so the point is in the second quadrant.
|
The value of ![]() is given by
is given by 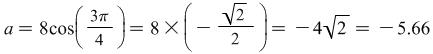 . The value of
. The value of ![]() is given by
is given by ![]() . The complex number in cartesian form is therefore
. The complex number in cartesian form is therefore ![]() .
.
iii) Both the cosine and sine terms are positive, and ![]() , so the point is in the fourth quadrant.
, so the point is in the fourth quadrant.
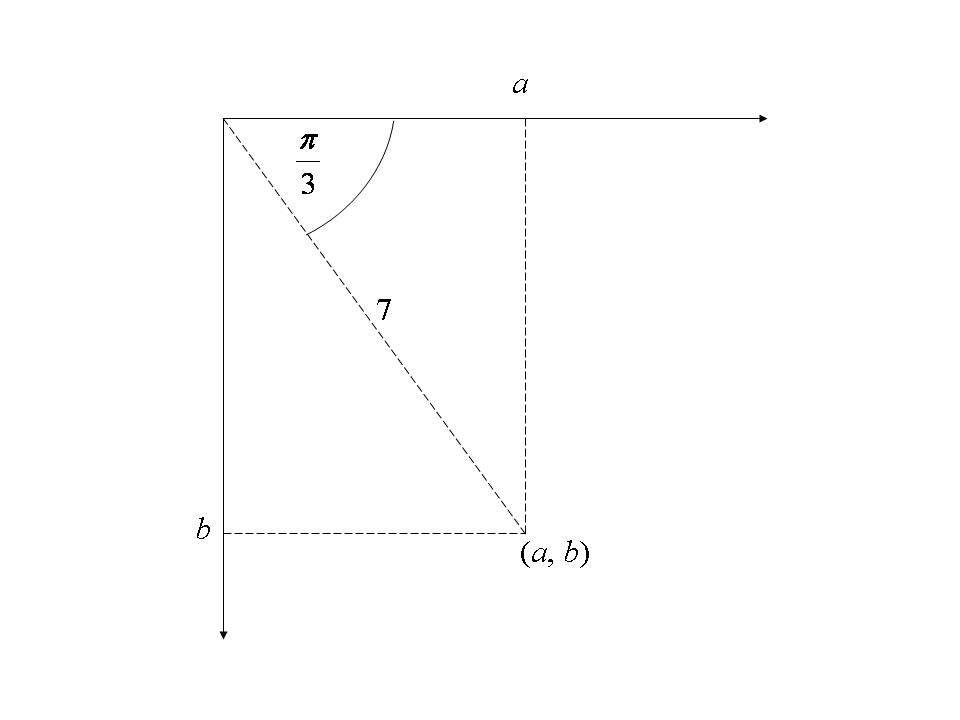
|
The value of ![]() is given by
is given by ![]() and the value of
and the value of ![]() is given by
is given by 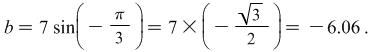
Therefore, in cartesian form, ![]() .
.