Vectors and matrices - basic

Example 1. Marices in Mathematica are presented as two dimensional lists by lines. Bellow a standard writing and   palettes are used. The matrix m is then multiplied by 3. Then the sum of matrices m and m1 is carried out.

m={{a,b},{c,d}}
3m

{{a, b}, {c, d}}

{{3 a, 3 b}, {3 c, 3 d}}

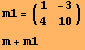
m1 = (1 -3) 4 10 m + m1

{{1, -3}, {4, 10}}

{{1 + a, -3 + b}, {4 + c, 10 + d}}

Example 2. Showing the list in the form of a table is done with the functions TableForm or MatrixForm:

u={{1,2},{0,1}};  
TableForm[%]
MatrixForm[u]
v={{3,1},{2,2}};  
TableForm[%]

1 2
0 1

( 1 2 ) 0 1

3 1
2 2

Example 3. Matrix product is marked with . (dot). The last out extract the element in the first line, second column by using the double brackets [[ ]].

pr=u.v
MatrixForm[%]
element=%[[1,2]]

{{7, 5}, {2, 2}}

( 7 5 ) 2 2

5

Example 4. Product of the matrix m and vector {x, y}:

m
r= m.{x,y}  
{x,y} .m
MatrixForm[r]

{{a, b}, {c, d}}

{a x + b y, c x + d y}

{a x + c y, b x + d y}

( a x + b y ) c x + d y

Example 5. We also have many special functions which calculate and generate particular matrix caracteristics, particular types of matrices and vectors, etc. For example finding the number of elements with the fucntion Length, creating lists with consecutive numbers with the function Range.

s1=Table[Exp[x],{x,0,1,0.25}]
Length[s1]    (* Gives the number of elements in the list *)
r6=Range[6]
Range[3,7]     (* Gives a list, containing the consecutive numbers from 3 to 7  *)
Range[3,7,0.5] (* The same, but with a step 0.5  *)

RowBox[{{, RowBox[{1, ,, 1.28403, ,, 1.64872, ,, 2.117, ,, 2.71828}], }}]

5

{1, 2, 3, 4, 5, 6}

{3, 4, 5, 6, 7}

RowBox[{{, RowBox[{3, ,, 3.5, ,, 4., ,, 4.5, ,, 5., ,, 5.5, ,, 6., ,, 6.5, ,, 7.}], }}]

Example 6. Standard creating of arrays with the function Array.  We clear the current values of some variables to avoid errors.

Clear[a,b,x,y]
Array[a,4]

{a[1], a[2], a[3], a[4]}

Example 7. More examples with formal arays - vectors and matrices:

Array[b,{4,1}]
MatrixForm[%]
Array[d,{3,3}]
d2=%
MatrixForm[d2]

{{b[1, 1]}, {b[2, 1]}, {b[3, 1]}, {b[4, 1]}}

( b[1, 1] ) b[2, 1] b[3, 1] b[4, 1]

{{d[1, 1], d[1, 2], d[1, 3]}, {d[2, 1], d[2, 2], d[2, 3]}, {d[3, 1], d[3, 2], d[3, 3]}}

{{d[1, 1], d[1, 2], d[1, 3]}, {d[2, 1], d[2, 2], d[2, 3]}, {d[3, 1], d[3, 2], d[3, 3]}}

( d[1, 1] d[1, 2] d[1, 3] ) d[2, 1] d[2, 2] d[2, 3] d[3, 1] d[3, 2] d[3, 3]

Example 8. It easy to obtain a identity matrix of arbitrary order, for instance of order 4.

id=IdentityMatrix[4]
MatrixForm[id]

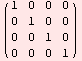
{{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}}

( 1 0 0 0 ) 0 1 0 0 0 0 1 0 0 0 0 1

Example 9. Creating a diagonal matrix and deducing the dimensions of a matrix.

DiagonalMatrix[Range[4]]
MatrixForm[%]
Dimensions[%]
Dimensions[m]

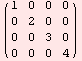
{{1, 0, 0, 0}, {0, 2, 0, 0}, {0, 0, 3, 0}, {0, 0, 0, 4}}

( 1 0 0 0 ) 0 2 0 0 0 0 3 0 0 0 0 4

{4, 4}

{2, 2}

Example 10. Easy obtantation of a diagonal matrix.

DiagonalMatrix[{-1,2,-3}]
MatrixForm[%]

{{-1, 0, 0}, {0, 2, 0}, {0, 0, -3}}

( -1 0 0 ) 0 2 0 0 0 -3

Example 11. Sorting the elements and other transformations.

k1={2,5,6,-2,4,4,1}
k2=Sort[k1]
x=. (*  Clear the current values and definitions of x and a *)
a=.
a=Table[x^(i+j),{i,0,2},{j,0,2}] (* Creating new matrix a by function Table *)
MatrixForm[a]

{2, 5, 6, -2, 4, 4, 1}

{-2, 1, 2, 4, 4, 5, 6}

{{1, x, x^2}, {x, x^2, x^3}, {x^2, x^3, x^4}}

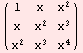
( 2 ) 1 x x 2 3 x x x 2 3 4 x x x

Example 12. Calculating determinants.

f={{5,3},{4,2}}; MatrixForm[f]
Det[f]

( 5 3 ) 4 2

-2

Example 13. Matrix differentiation.

a ∂_x a

{{1, x, x^2}, {x, x^2, x^3}, {x^2, x^3, x^4}}

{{0, 1, 2 x}, {1, 2 x, 3 x^2}, {2 x, 3 x^2, 4 x^3}}

a
D[a,x]

{{1, x, x^2}, {x, x^2, x^3}, {x^2, x^3, x^4}}

{{0, 1, 2 x}, {1, 2 x, 3 x^2}, {2 x, 3 x^2, 4 x^3}}

Created by Mathematica  (December 21, 2007)