Infinite numeric series and power series expansions:
Series, Normal, Simplify and other functions.

Example 1. Generating a power series expansion of a given function by the build-in function Series[ ].  Here we expand the function (1 + x)^n about the point 0 (standard Taylor serie) to order 5. The form of the rеsidual member is also given.

Series[(1 + x)^n, {x, 0, 5}]

1 + n x + 1/2 (-1 + n) n x^2 + 1/6 (-2 + n) (-1 + n) n x^3 + 1/24 (-3 + n) (-2 + n) (-1 + n) n x^4 + 1/120 (-4 + n) (-3 + n) (-2 + n) (-1 + n) n x^5 + O[x]^6

  Power series expansion for the same function about the point 1. To show it without the residual member we use the function Normal[ ].

Series[(1 + x)^n, {x, 1, 5}] red1 = Normal[%]

2^n + 2^(-1 + n) n (x - 1) + 2^(-3 + n) (-1 + n) n (x - 1)^2 + 1/3 2^(-4 + n) (-2 + n) (-1 + n ... -1 + n) n (x - 1)^4 + 1/15 2^(-8 + n) (-4 + n) (-3 + n) (-2 + n) (-1 + n) n (x - 1)^5 + O[x - 1]^6

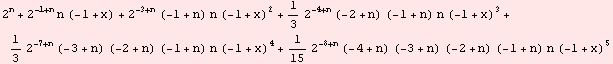
2^n + 2^(-1 + n) n (-1 + x) + 2^(-3 + n) (-1 + n) n (-1 + x)^2 + 1/3 2^(-4 + n) (-2 + n) (-1 + ... (-2 + n) (-1 + n) n (-1 + x)^4 + 1/15 2^(-8 + n) (-4 + n) (-3 + n) (-2 + n) (-1 + n) n (-1 + x)^5

Example 2.  Taylor series expansion for the function ^x.

Series[^x, {x, 0, 7}]

1 + x + x^2/2 + x^3/6 + x^4/24 + x^5/120 + x^6/720 + x^7/5040 + O[x]^8

The same as Example 2,  but written in standard form.

Series[Exp[x],{x,0,7}]
Normal[%]

1 + x + x^2/2 + x^3/6 + x^4/24 + x^5/120 + x^6/720 + x^7/5040 + O[x]^8

1 + x + x^2/2 + x^3/6 + x^4/24 + x^5/120 + x^6/720 + x^7/5040

Example 3. Power series expansion of a trigonometric function. Showing the result with decimal fractions shows how fast the coefficients tend towards zero.

Series[Sin[2t],{t,0,20}]
N[Normal[%]]

2 t - (4 t^3)/3 + (4 t^5)/15 - (8 t^7)/315 + (4 t^9)/2835 - (8 t^11)/155925 + (8 t^13)/6081075 - (16 t^15)/638512875 + (4 t^17)/10854718875 - (8 t^19)/1856156927625 + O[t]^21

RowBox[{RowBox[{2., , t}], -, RowBox[{1.33333, , t^3}], +, RowBox[{0.266667, , t^5}], -, Ro ... 582*10^-8, , t^15}], +, RowBox[{3.68503*10^-10, , t^17}], -, RowBox[{4.30998*10^-12, , t^19}]}]

Example 4. Here Mathematica will multiply two power series in advance and will show the expansion of the obtained function. We can use the function Simplify[ ] to get some simplification.

Series[^(t + 1) Sin[2t], {t, 0, 7}] Normal[%] Simplify[%] %//N Simplify[%]

2  t + 2  t^2 - ( t^3)/3 -  t^4 - (19  t^5)/60 + (11  t^6)/180 + (139  t^7)/2520 + O[t]^8

2  t + 2  t^2 - ( t^3)/3 -  t^4 - (19  t^5)/60 + (11  t^6)/180 + (139  t^7)/2520

( t (5040 + 5040 t - 840 t^2 - 2520 t^3 - 798 t^4 + 154 t^5 + 139 t^6))/2520

RowBox[{0.00107868, , t, , RowBox[{(, RowBox[{RowBox[{5040., }], +, RowBox[{5040., ... , t^3}], -, RowBox[{798., , t^4}], +, RowBox[{154., , t^5}], +, RowBox[{139., , t^6}]}], )}]}]

RowBox[{0.149937, , RowBox[{(, RowBox[{RowBox[{-, 2.77144}], +, t}], )}], , RowBox[{(, RowBo ... )}], , RowBox[{(, RowBox[{RowBox[{2.08743, }], +, RowBox[{2.818, , t}], +, t^2}], )}]}]

Example 5. Formal power series expansions with functions in the form of formulas.

Clear[a,f]
Series[f[t],{t,0,5}]
Series[f[t],{t,a,5}]

f[0] + f^′[0] t + 1/2 f^′′[0] t^2 + 1/6 f^(3)[0] t^3 + 1/24 f^(4)[0] t^4 + 1/120 f^(5)[0] t^5 + O[t]^6

f[a] + f^′[a] (t - a) + 1/2 f^′′[a] (t - a)^2 + 1/6 f^(3)[a] (t - a)^3 + 1/24 f^(4)[a] (t - a)^4 + 1/120 f^(5)[a] (t - a)^5 + O[t - a]^6

Example 6. Unspecified transformations with series are possible.

red2=Normal[Series[Tan[-a*x]*(1+Cos[2x]),{x,0,4}]]
red3=red2 *2 *(1-red2)
Simplify[%]

-2 a x + (2 a - (2 a^3)/3) x^3

2 (1 + 2 a x - (2 a - (2 a^3)/3) x^3) (-2 a x + (2 a - (2 a^3)/3) x^3)

-4/9 a x (3 + (-3 + a^2) x^2) (3 + 2 a^3 x^3 - 6 a x (-1 + x^2))

Example 7. In the obtained expansion in the upper example we can group the members according to ' x ' or ' a '. In the before last operator calculates the tangible value at a=1, whereas in the last a=1 and x=2 are replaced by using the symbol ' /. ' (forward inclined line and dot).

red4 = Collect[red3, x] Collect[red3, a] %/.a1//N RowBox[{RowBox[{red4, /., , RowBox[{{, RowBox[{RowBox[{a, , 1.}], ,, , RowBox[{x, , 2.}]}], }}]}], //, N}]

-4 a x - 8 a^2 x^2 + 2 (2 a - (2 a^3)/3) x^3 + 8 a (2 a - (2 a^3)/3) x^4 - 2 (2 a - (2 a^3)/3)^2 x^6

-4/3 a^3 x^3 - (8 a^6 x^6)/9 + 2 a (-2 x + 2 x^3) + 2 a^2 (-4 x^2 + 8 x^4 - 4 x^6) + 2 a^4 (-(8 x^4)/3 + (8 x^6)/3)

RowBox[{RowBox[{RowBox[{-, 1.33333}], , x^3}], -, RowBox[{0.888889, , x^6}], +, RowBox[{2., ... RowBox[{(, RowBox[{RowBox[{RowBox[{-, 2.66667}], , x^4}], +, RowBox[{2.66667, , x^6}]}], )}]}]}]

RowBox[{-, 75.5556}]

Example 8. Series for functions of two variables.

Series[Sin[x + y^2], {x, 0, 7}, {y, 0, 7}] Normal[%] Series[Sin[^x], {x, 0, 7}, {y, 0, 5}] Simplify[%]

(y^2 - y^6/6 + O[y]^8) + (1 - y^4/2 + O[y]^8) x + (-y^2/2 + y^6/12 + O[y]^8) x^2 + (-1/6 + y^4 ... 0 + O[y]^8) x^5 + (-y^2/720 + y^6/4320 + O[y]^8) x^6 + (-1/5040 + y^4/10080 + O[y]^8) x^7 + O[x]^8

x - x^3/6 + x^5/120 - x^7/5040 + (1 - x^2/2 + x^4/24 - x^6/720) y^2 + (-x/2 + x^3/12 - x^5/240 + x^7/10080) y^4 + (-1/6 + x^2/12 - x^4/144 + x^6/4320) y^6

Sin[1] + Cos[1] x + (Cos[1]/2 - Sin[1]/2) x^2 - 1/2 Sin[1] x^3 + (-(5 Cos[1])/24 - Sin[1]/4) x ... x^5 + (-(37 Cos[1])/360 + (11 Sin[1])/240) x^6 + (-(23 Cos[1])/720 + (19 Sin[1])/360) x^7 + O[x]^8

Sin[1] + Cos[1] x + 1/2 (Cos[1] - Sin[1]) x^2 - 1/2 Sin[1] x^3 + 1/24 (-5 Cos[1] - 6 Sin[1]) x ... - 5 Sin[1]) x^5 + 1/720 (-74 Cos[1] + 33 Sin[1]) x^6 + 1/720 (-23 Cos[1] + 38 Sin[1]) x^7 + O[x]^8

Example 9. Series can be manipulated like expressions:

s1 = (Series[Log[1 + x], {x, 0, 5}] + Series[Sin[2 x], {x, 0, 5}]/Series[Cos[3x], {x, 0, 5}])^3 s2 = s1^(1/2) s3 = ∫_0^π/4s1x s4 = ∂_x s1

27 x^3 - (27 x^4)/2 + (873 x^5)/4 - (631 x^6)/8 + (13461 x^7)/10 + O[x]^8

3 3^(1/2) x^(3/2) - 3/4 3^(1/2) x^(5/2) + 385/32 3^(1/2) x^(7/2) - (1583 x^(9/2))/(384 3^(1/2)) + (4636997 x^(11/2))/(30720 3^(1/2)) + O[x]^(13/2)

27/4 (π/4)^4 - 27/10 (π/4)^5 + 291/8 (π/4)^6 - 631/56 (π/4)^7 + 13461/80 (π/4)^8 + O[π/4]^9

81 x^2 - 54 x^3 + (4365 x^4)/4 - (1893 x^5)/4 + (94227 x^6)/10 + O[x]^7

Example 10. Series can be invesed by InverseSeries[ ] build-in function.

s5 = Series[^x, {x, 0, 5}] s5i = InverseSeries[s5] ss = s5/. xs5i Normal[ss]

1 + x + x^2/2 + x^3/6 + x^4/24 + x^5/120 + O[x]^6

1 - x + x^2/2 - x^3/6 + x^4/24 - x^5/120 + O[x]^6

(x - 1) - 1/2 (x - 1)^2 + 1/3 (x - 1)^3 - 1/4 (x - 1)^4 + 1/5 (x - 1)^5 + O[x - 1]^6

1 + (x - 1) + O[x - 1]^6

x

Created by Mathematica  (December 21, 2007)