calculus1

Calculus: derivatives, integrals and limits

Example 1. We set a polynom symbolically. First and third derivatives with respect to x are obtained.

f=x^5-2x^3-1
D[f,x]
D[f,{x,3}]

The same commands can be written with the help of palettes for mathematical symbols. If we use f' then we will recieve it as a substitution. То calculate the derivative we use . For the third derivative we add another x :

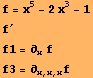
f = x^5 - 2x^3 - 1 f^′ f1 = ∂_x f f3 = ∂_ (x, x, x) f

One can reperesent all functions by a declaration like this:

h[x_] := x^5 - 2x^3 - 1 ∂_x h[x] h[1]

Example 2. Let us see the graphics of the derived functions from Example 1. Obviously interesting is the behaviour in the interval [-2,2] which is why we show the derivatives only in this interval.

g1 = Plot[f, {x, -5, 5}] g2 = Plot[f1, {x, -2, 2}] g3 = Plot[f3, {x, -2, 2}]

[Graphics:HTMLFiles/index_14.gif]

[Graphics:HTMLFiles/index_16.gif]

[Graphics:HTMLFiles/index_18.gif]

Example 3. We define a function of two variables. The partial derivatives with respect to x is found, then to y, in the end - the mixed derivative .

g[x_, y_] := 7x^2 - y^3 - Log[x] ∂_x g[x, y] ∂_y g[x, y] ∂_ (x, y) g[x, y]

Example 4. The variable f is nullified. We define the symbolical derivative.

f = .
D[f[x],x]
D[5* x *f[x], x]

Example 5. A new value is set to f, the old one is deleted automatically. An undefined integral is derived. In the end - a defined integral: a precise value and an approximate value.

f = (1 - 2x^3)/(2 + 3x) ∫fxIntegrate[f, x] &nb ... (* Here the symbol % takes the preceding result *)

Example 6. We set a function with the name newf. The derivative with respect to x and a double integral are calculated. Ultimately the result is given numerically.

newf[x_, y_] := x^4 + 3y d = ∂_x newf[x, y] ∫_0^1∫_1^2newf[x, y] yx %//N

Example 7. We set a trigonometric function. We want to carry out the definite integral, but the system is having difficulties, because we have singularities in the function Cos[ ]. Despite the slow calculations we get a result. If calculations are too slow we can interrupt them by pressin ALT + . or from the Kernel/Abort Evaluation menu.

f=. f[x_, y_] := Cos[( x)/y] ∫_0^π∫_0^πf[x, y] xy ... , π}] (* Approximate integration by numerical method *)

NIntegrate :: slwcon : Numerical integration converging too slowly; suspect one of the followi ... r integrand is oscillatory try using the option Method->Oscillatory in NIntegrate. More…

Example 8. Here we show the graphics of the function from the previous example so that the singularities can be seen.

Plot3D[f[x,y],{x,0,1},{y,0,1}]

[Graphics:HTMLFiles/index_60.gif]

Example 9. New function and calculation of an integral with inconsistant boundaries.

f=. ; f = x^2 + 1/(1 + y^2) ∫_0^1∫_0^x^(1/2) fyx N[%]

Exampleр 10. This is an example of a triple integral. First the exact and then the approximate values are found. The latter is shown with double accuracy.

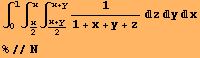
∫_0^1∫_x/2^x∫_ (x + y)/2^(x + y) 1/(1 + x + y + z) zyx %//N

The upper example can be set in a usual way like this:

f= 1/(1+x+y+z)
Integrate[f,{x,0,1},{y,x/2,x},{z,(x+y)/2,x+y}]
N[%]

Example 11. Let us examine another function with singularities. The system does not find it difficult to draw the graphics even though in the point x=0 the function is not defined. Due to the large gap however, in a larger interval the zero is skipped.

f = Sin[x]/x Plot[f, {x, 0, 10}] Plot[f, {x, 0, 100}]