tour-p5.nb

Calculations

Mathematica allows for easy combination and activation of different built- in functions and standard packeges, so all types of complex problems can be solved. The system has strong internal rules, completely corresponding to mathematical rules. Naturally it posesses the rules for differentiating, integrating and other symbolic operations as well as many tables and special functions. At the same time we can also define and operate with our own rules. This abstraction will be cleaner when numeric expressions are calculated due to the different types of numbers and accuracies we work with.

Example 1. It is important to note that Mathematica always TRIES to calculate as accurately as possible while applying the allowed mathematical rules. For this it must be clear that the result type is the same as the data type. Numeric constants and variables can be integer, rational, real, complex, etc. This type is easiest set implicitely, in other word according to the numbers and variables which are in the operator. For example 123 is an integer number and 123. is a real number. It is enough for only one data to be of a higher type to change the result type. Below are the simplest cases of changing from one type to another as well as for their calculating aspects.

Here the data is of type integer and Mathematica works accurately:

Now the types become real and the same actions are carried out in decimals, with six symbols after the decimal point by default:

$pn = N[p] rn = pn/12 rn^(1/2) RowBox[{RowBox[{1., /, 3}], +, 1/4}]$

In order to work with complex numbers an imaginary unit i is set, but the constants can be integer or real. The functions Re[x1 ] and Im[ x1] give the real and imaginary parts of the complex number x1, respectively:

$x1 = (1 + 2)/(5 - 3) RowBox[{x2, =, RowBox[{RowBox[{(, RowBox[{1., +, 2}], )}], /, (5 - 3)}]}] Re[x1] Im[x1] (x1^2 * x2)^(1/3)$

Example 2. The matrix is a typical example of a two dimensional array. In Mathematica arrays are presented easiest in the form of embedded lists. In the first internal curly brackets are the first line elements, in the second - the second line etc. The function MatrixForm[ ] shows a standard matrix form. Extracting a separate element is done with double square brackets, as shown on the lower line of the example.

a = {{2, 4, 5}, {1, -8, 2}, {3, 7, 4}} MatrixForm[a] a[[1, 1]] a[[3, 2]]

Example 3. The function Eigenvalues[ ] calculates the eigenvalues of the matrix a from Example 2. The result is again returned as a list, but a list of rules, because the given matrix elements are integers, but the result is not. The problem is solved by changing the type beforehand by means of the build-in function N[ ].

z = Eigenvalues[a] ra = N[a] z = Eigenvalues[ra]

${Root[-23 - 68 #1 + 2 #1^2 + #1^3&, 1], Root[-23 - 68 #1 + 2 #1^2 + #1^3&, 3], Root[-23 - 68 #1 + 2 #1^2 + #1^3&, 2]}$

Example 4. A way to generate matrices is through the function Table[ ]. This is how we can get the Wandermond matrix and calculate its determinant. The last line simplifies the result.

$v = Table[x_i^j, {j, 0, 4}, {i, 5}] MatrixForm[v] Det[v] ; dvan = Simplify[%]$

${{1, 1, 1, 1, 1}, {x_1, x_2, x_3, x_4, x_5}, {x_1^2, x_2^2, x_3^2, x_4^2, x_5^2}, {x_1^3, x_2^3, x_3^3, x_4^3, x_5^3}, {x_1^4, x_2^4, x_3^4, x_4^4, x_5^4}}$

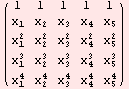
( ) 1 1 1 1 1 x x ... 4 4 4 4 4 x x x x x 1 2 3 4 5

Example 5. Similarly to Example 4 we will generate a matrix with elements which are undefined integrals and we will calculate its determinant:

w = Table[∫ (Cos[t] * Sin[t])/(i + j) t, {j, 3}, {i, 3}] ; ws = Simplify[%] ; MatrixForm[ws] dw = Det[ws] %//N

( 1 2 1 2 1 2 ) -- Cos[t] -- Cos[t] ... 2 -- Cos[t] --- Cos[t] --- Cos[t] 8 10 12

$RowBox[{RowBox[{-, 2.89352*10^-6}], , Cos[t]^6}]$

Example 6. The derivative of the result from Example 5 is saved as the variable f, is simplified and we draw the graphics in the interval [ -π, π ]:

$f = ∂_tdw f = TrigReduce[f] Plot[f, {t, -π, π}]$

[Graphics:HTMLFiles/index_37.gif]

Example 7. Below are the local minima and maxima of the upper functin f in the area closest to the point t = 2.5 - the minimum is at t = 2.72106 and the maximum is at t = 0.420534.

$RowBox[{{, RowBox[{RowBox[{-, 4.49313*10^-6}], ,, RowBox[{{, RowBox[{t, , 2.72106}], }}]}], }}]$

$RowBox[{{, RowBox[{4.49313*10^-6, ,, RowBox[{{, RowBox[{t, , 0.420534}], }}]}], }}]$

Example 8. Now we expend f in Taylor serie at point 0 to order 10.

Example 9. Here a non-trivial integral is calculated. To do that a dot is added after at least one constant, i.e. 3., which leads that all calculations are made in type real. In order to follow the behaviour of the function it is a good idea to have also its graphics.

$RowBox[{g, =, RowBox[{(1 + x^3), /, RowBox[{(, RowBox[{x^4, +, RowBox[{3., x^2}], -, 5x, +, 2} ... (1 + x^3), /, RowBox[{(, RowBox[{x^4, +, RowBox[{3., x^2}], -, 5x, +, 2}], )}]}], x}]}]}]$

$RowBox[{(1 + x^3), /, RowBox[{(, RowBox[{2, -, 5 x, +, RowBox[{3., , x^2}], +, x^4}], )}]}]$

[Graphics:HTMLFiles/index_46.gif]

$RowBox[{RowBox[{RowBox[{-, 1.18128}], , RowBox[{ArcTan, [, RowBox[{RowBox[{3.5056, }] ... RowBox[{Log, [, RowBox[{RowBox[{4.2655, }], +, RowBox[{1.31696, , x}], +, x^2}], ]}]}]}]$

Created by Mathematica (October 6, 2007)