Algorithms in Mathematica      

The Mathematica system posesses the largest collection of built-in algorithms for exact and approximate calculation of problems, represented as functions. The most among them are numeric calculations of roots of equations and systems of equations, matrix inversion , eigenvalues of a matrix, problems in number theory, numerical and symbolic integration, solving differential equations etc.
When there is no built-in function we can search for appropriate standard add-on Mathematica package or program an unspecified algorithm ourselves by using the corresponding operators from the highly evolved programming language of Mathematica.

Example 1. Build-in function for Newton's method for solving trancendental equations. In the example bellow a real root of the equation Cos(x)=x+Log(x) is found, by using x=1 as initial guess. It is better to combine the solution with a graphics in the correct interval.

For a desidered plot we must represent the equation in the form f=0 and give some interval. Near we see that the root is in the interval [0,1]. Sometimes the function FindRoot implies more precise initial guess.

Example 2. Aprroximate solutions of equations and systems of equations, including those in a complex plane. Exact solutions are found with the function Solve[ ], if possible. If it does not give a result it will try with build-in algorithims for numerical solving: NSolve[ ],  FindRoot[ ], Reduce[ ] and other functions. Here we solve a polinomial equation in complex plane with regard of x with an accuracy of 30 arithmetic symbols. In this case we simultaniously recieve five different real roots in the form of a list (in curly brackets).

Example 3. To pick out one of the roots we could use the following expressions (here for the second and the last root):

Example 4. Calculation of the approximate value of a certain integral. Capital 'N' in front of the function Integrate shows that it is calculated numerically (from Numerical). The two lines give the same result. By clicking the output line and pressing ENTER the result is shown with 16 digits accuracy.

Example 5. Factorization of an integer in prime factors. The result is shown in the form of a list where the furst number is the prime factor and the second -its exponent. The first output gives that  18=or  2.9=18. The second means that n=172872 is factorize in prime factors as .

Example 6. Setting a square matrix a , the sytem finds its inversion b. The third matrix  c demonstrates the verification, that  a.b gives the identity matrix.

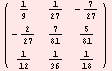
Example 7. Mathematica solves differential equations and systems symbolically (when possible) as well as numerically. Here is a non-linear second-order ordinary differential equation  with inital conditions at point 0.
                 x'' + = sin(t),    x(0) = 0,  x'(0) = 0,   t ∈ [0, 20]
The algorithim for approximate solving is called on by the function NDSolve. With numerical solving we recieve a table of values which the system remembers as an integrating function. The way to graphically display the result is shown in a different cell.

Example 8. Mathematica solves inequalities and plots graphics of the solutions. The appropriate algoritms are included in a special packages. In this example we solve an algebraic system of two inequalities. To avoid a possible reuse of common variables we first clear the contents of x, y and t by the function Clear[]. The second line loads the package.

Below the sign && means the logical AND operator and the sign || means the logical OR operator.

Example 9. Now a system of two inequalities in a 2D is solved.

Example 10. And finally the 2D graphics of the solution from example 9 is plotted. The package is loaded beforhand.

Created by Mathematica  (October 6, 2007)