Mathematica as a calculator                               

You can use Mathematica as an ordinary calculator - type in an expression, press SHIFT + ENTER  and  Mathematica calculates it and gives you the result.
Near the main work rules are ubderlined.

Example 1. Raising the number 3 to the 2th power. You can choose different values if you wish. On the right end of the line the cell is marked by a blue squared bracket . When the cursor is blinking in the cell, press the  SHIFT+ENTER keys simultaniousley. You can go back and execute any chosen cell at any time.  

Mathematica automatically works with infinite accuracy, for example 3 to the 100th power is a number with 48 decimal symbols:

Yu can choose mathematical symbols similarly to WORD by using the palettes. For example open from the menu: File \ Palettes \ BasicInput, so that the previous example can be also written as:

Example 2. We can use variables to store numbers, graphics, lists or any other Mathematica object. But be very careful in naming variables, because the capital letters are different from the miniscule letters.  For instance variables A1 and a1 contain different object:

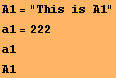
Example 3. Two or more expressions can be placed in a single cell and can be executed one after the other. Here is a scalar product of two vectors a and b, whoose components are given in curly brackets. The result will be stored in variable c. Keep in mind that the dot between them as a vector product symbol is manditory.

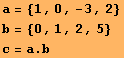
Example 4. Standard mathematical constants and build-in funcions are written with a capital first letter and the argument in square brackets. Note that Mathematica is case sensitive!  You can use palettes as well.

Example 5. When we want the result to be a number it is enough to give at least one argument as a decimal fraction, i.e.  2.0,  -12.456,  100.  etc. Note the difference:

Example 6. It is easy to input formulas. When the variables in them have recieved a result beforehand Mathematica will work with numbers, otherwise it will work with symbols. We are going to solve a quadratic equation now and an irrational parametric equation with a parameter k - later. Note that in equations the symbol for logical comparison = = is used , and not the regular equation symbol =.

Saving solutions for later use is shown below. Here /. is a symbol for substitute. The % takes the result from the previous command.

Example 8. Let us calculate an indefinite integral by choosing the correct integral symbol from the mathematical symbol palette File \ Palettes \ BasicInput. In order to use the variable a as a parameter we need to cancel it since that letter was used in example 2 as a vector. This cancelation is carried out by the symbol  =. (dot):

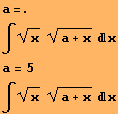
Example 9. Let us see what is the graphics of the integrand function  f= where а=5 in the interval [0, 1] for example.

Example 10. Here is the definite integral of the same integrand function in the interval [0,1] for a=7.  In order to avoid output value of a, we need to add the symbol ; (semicolon).

Example 11. Bellow we draw a two-dimentional graphics of the function sin (2.5x) + cot (x)  in  the interval [-3π, 2π]. Here Cot[x] is the cotangent function. Then the same graphics is given, but the values of the function are limited between -2 and 2. The vertical asymptotes are drown too.

Example 12. We can draw several graphics around a single axis:

Example 13. An example of a 3D graphics in Cartesian coordinates when the function is given by a formulae. Bordsers for values must be set every time, so that the system can calculate the needed values. We have added an option for specifying the number of points in the two directions of the net which draw the graphics.

Example 14. Another example of a 3D graphics with a set function formula. When there are asymptotes, Mathematica tries to draw them. In the following example the function Cot (cotangent) is undefined when y=0, which is why there is a отвесна равнина (област на прекъсване).

Created by Mathematica  (October 6, 2007)