Application of the derivative for proving identities, inequalities and solving equations

Aim: Broadening students' knowledge about the potential of first and second derivative of a function

Application: Proving some types of identities and inequalities as well as solving equations

Presentation structure:
Proving identities using a derivative

algebra identities
problems for individual work
trigonometric problems
problems for individual work

1 Proving identities using derivatives

The basic theorem

Theorem 1.1. If a function $tema7_EN_files\tema7_EN_MathML_0.jpg$ is defined and differentiable in the interval $tema7_EN_files\tema7_EN_MathML_1.jpg$ and for every $tema7_EN_files\tema7_EN_MathML_2.jpg$ , then $tema7_EN_files\tema7_EN_MathML_3.jpg$ is a constant in $tema7_EN_files\tema7_EN_MathML_4.jpg$ .

Corollary 1.2. If differentiable in the interval $tema7_EN_files\tema7_EN_MathML_5.jpg$ functions $tema7_EN_files\tema7_EN_MathML_6.jpg$ and $tema7_EN_files\tema7_EN_MathML_7.jpg$ have equal derivatives everywhere in $tema7_EN_files\tema7_EN_MathML_8.jpg$ , then they differ with a constant, i.e. if $tema7_EN_files\tema7_EN_MathML_9.jpg$ , for every $tema7_EN_files\tema7_EN_MathML_10.jpg$ , then $tema7_EN_files\tema7_EN_MathML_11.jpg$ , $tema7_EN_files\tema7_EN_MathML_12.jpg$ - a constant.

We take on trust the truthfulness of the theorem above.

Identity

Definition 1.3. Two expressions $tema7_EN_files\tema7_EN_MathML_13.jpg$ and $tema7_EN_files\tema7_EN_MathML_14.jpg$ (rational or irrational) are called identical in a given set $tema7_EN_files\tema7_EN_MathML_15.jpg$ , in which $tema7_EN_files\tema7_EN_MathML_16.jpg$ and $tema7_EN_files\tema7_EN_MathML_17.jpg$ are defined if for all values of variables from $tema7_EN_files\tema7_EN_MathML_18.jpg$ their numerical values are equal. Then the equality $tema7_EN_files\tema7_EN_MathML_19.jpg$ is called identity. Usually for $tema7_EN_files\tema7_EN_MathML_20.jpg$ is used the set of admissible values of the equality $tema7_EN_files\tema7_EN_MathML_21.jpg$ .

There are several ways to prove that the equality $tema7_EN_files\tema7_EN_MathML_22.jpg$ is identical with the given set $tema7_EN_files\tema7_EN_MathML_23.jpg$ :

If the expression $tema7_EN_files\tema7_EN_MathML_24.jpg$ is more complex it is transformed into an identical expression $tema7_EN_files\tema7_EN_MathML_25.jpg$ (in the set $tema7_EN_files\tema7_EN_MathML_26.jpg$ ), after that $tema7_EN_files\tema7_EN_MathML_27.jpg$ - in an identical to it $tema7_EN_files\tema7_EN_MathML_28.jpg$ and so on until after a finite number of transformations ( for example $tema7_EN_files\tema7_EN_MathML_29.jpg$ ) the expression $tema7_EN_files\tema7_EN_MathML_30.jpg$ is identical to $tema7_EN_files\tema7_EN_MathML_31.jpg$ , i.e. $tema7_EN_files\tema7_EN_MathML_32.jpg$ . This leads to the conclusion $tema7_EN_files\tema7_EN_MathML_33.jpg$
The difference $tema7_EN_files\tema7_EN_MathML_34.jpg$ is transformed into an identical to it expression $tema7_EN_files\tema7_EN_MathML_35.jpg$ , then $tema7_EN_files\tema7_EN_MathML_36.jpg$ into an identical to it expression $tema7_EN_files\tema7_EN_MathML_37.jpg$ and so on until it is proven that $tema7_EN_files\tema7_EN_MathML_38.jpg$ is identically equal to zero, i.e. $tema7_EN_files\tema7_EN_MathML_39.jpg$ . From here $tema7_EN_files\tema7_EN_MathML_40.jpg$ , i.e. $tema7_EN_files\tema7_EN_MathML_41.jpg$ .
The expressions $tema7_EN_files\tema7_EN_MathML_42.jpg$ and $tema7_EN_files\tema7_EN_MathML_43.jpg$ are simultaneously transformed into respective identical $tema7_EN_files\tema7_EN_MathML_44.jpg$ and $tema7_EN_files\tema7_EN_MathML_45.jpg$ . Further on $tema7_EN_files\tema7_EN_MathML_46.jpg$ and $tema7_EN_files\tema7_EN_MathML_47.jpg$ into $tema7_EN_files\tema7_EN_MathML_48.jpg$ and $tema7_EN_files\tema7_EN_MathML_49.jpg$ and so on until $tema7_EN_files\tema7_EN_MathML_50.jpg$ and $tema7_EN_files\tema7_EN_MathML_51.jpg$ become apparently equal i.e. $tema7_EN_files\tema7_EN_MathML_52.jpg$ .

Of bigger interest to us is the second method. There are cases when using traditional means (from elementary mathematics) it is hard or impossible to directly prove that $tema7_EN_files\tema7_EN_MathML_53.jpg$ . But it is possible (by means of a special technique) to show first that $tema7_EN_files\tema7_EN_MathML_54.jpg$ , and then that this $tema7_EN_files\tema7_EN_MathML_55.jpg$ is equal to zero.

Algorithm

When proving identities of the kind $tema7_EN_files\tema7_EN_MathML_56.jpg$ we implement the following algorithm:

We consider the function $tema7_EN_files\tema7_EN_MathML_57.jpg$ where $tema7_EN_files\tema7_EN_MathML_58.jpg$ are parameters.
We prove that $tema7_EN_files\tema7_EN_MathML_59.jpg$ for every admissible value of $tema7_EN_files\tema7_EN_MathML_60.jpg$ .
We determine that $tema7_EN_files\tema7_EN_MathML_61.jpg$ where $tema7_EN_files\tema7_EN_MathML_62.jpg$ is a randomly chosen number from the admissible values of $tema7_EN_files\tema7_EN_MathML_63.jpg$ .
On the basis of theorem 1.1 we conclude that $tema7_EN_files\tema7_EN_MathML_64.jpg$ for every admissible $tema7_EN_files\tema7_EN_MathML_65.jpg$ . Consequently $tema7_EN_files\tema7_EN_MathML_66.jpg$ .

1.1 Proving algebra identities

Example 1.4. Prove the identity $tema7_EN_files\tema7_EN_MathML_67.jpg$ for every xq a is a constant.

Solution: Let $tema7_EN_files\tema7_EN_MathML_68.jpg$ .

$tema7_EN_files\tema7_EN_MathML_69.jpg$

$tema7_EN_files\tema7_EN_MathML_70.jpg$

$tema7_EN_files\tema7_EN_MathML_71.jpg$ . When $tema7_EN_files\tema7_EN_MathML_72.jpg$ , $tema7_EN_files\tema7_EN_MathML_73.jpg$

$tema7_EN_files\tema7_EN_MathML_74.jpg$ .

Example 1.5. Prove the identity $tema7_EN_files\tema7_EN_MathML_75.jpg$ for every x, y.

Solution: Let $tema7_EN_files\tema7_EN_MathML_76.jpg$ .

$tema7_EN_files\tema7_EN_MathML_77.jpg$

$tema7_EN_files\tema7_EN_MathML_78.jpg$

$tema7_EN_files\tema7_EN_MathML_79.jpg$ .

When $tema7_EN_files\tema7_EN_MathML_80.jpg$ . Consequently $tema7_EN_files\tema7_EN_MathML_81.jpg$ .

Example 1.6. Prove the identity $tema7_EN_files\tema7_EN_MathML_82.jpg$ for every x, y, z.

Solution:

$tema7_EN_files\tema7_EN_MathML_83.jpg$

$tema7_EN_files\tema7_EN_MathML_84.jpg$

$tema7_EN_files\tema7_EN_MathML_85.jpg$ $tema7_EN_files\tema7_EN_MathML_86.jpg$

$tema7_EN_files\tema7_EN_MathML_87.jpg$

It is apparent that for most of these problems using derivatives leads to lowering of exponents of the expressions and so eases calculations.
The basic theorem can be used for proving the following identities.

Example 1.7. $tema7_EN_files\tema7_EN_MathML_88.jpg$ , if $tema7_EN_files\tema7_EN_MathML_89.jpg$

This problem represents a conditional identity which is a corollary of Example 1.6. In this case we offer a different solution.

Solution: From $tema7_EN_files\tema7_EN_MathML_90.jpg$ . Considering the function

$tema7_EN_files\tema7_EN_MathML_91.jpg$

$tema7_EN_files\tema7_EN_MathML_92.jpg$

Consequently $tema7_EN_files\tema7_EN_MathML_93.jpg$ . When $tema7_EN_files\tema7_EN_MathML_94.jpg$ if $tema7_EN_files\tema7_EN_MathML_95.jpg$ .

Example 1.8. Prove the identity $tema7_EN_files\tema7_EN_MathML_96.jpg$ for every a, b, c.

Solution: Let $tema7_EN_files\tema7_EN_MathML_97.jpg$

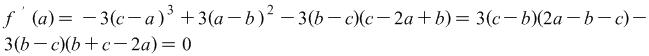
$tema7_EN_files\tema7_EN_MathML_98.jpg$

Consequently $tema7_EN_files\tema7_EN_MathML_99.jpg$ . When $tema7_EN_files\tema7_EN_MathML_100.jpg$ .

Example 1.9.

Prove the identity

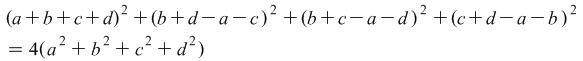
$tema7_EN_files\tema7_EN_MathML_101.jpg$

Hint: Let the function considered be $tema7_EN_files\tema7_EN_MathML_102.jpg$ .

Example 1.10. Prove the identity $tema7_EN_files\tema7_EN_MathML_103.jpg$ for every a, b, c.

Solution: $tema7_EN_files\tema7_EN_MathML_104.jpg$

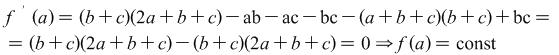
$tema7_EN_files\tema7_EN_MathML_105.jpg$

When $tema7_EN_files\tema7_EN_MathML_106.jpg$ $tema7_EN_files\tema7_EN_MathML_107.jpg$

Example 1.11. Prove the identity $tema7_EN_files\tema7_EN_MathML_108.jpg$ for every a, b, c.

Solution: Let $tema7_EN_files\tema7_EN_MathML_109.jpg$

$tema7_EN_files\tema7_EN_MathML_110.jpg$ .

When $tema7_EN_files\tema7_EN_MathML_111.jpg$ .

Consequently $tema7_EN_files\tema7_EN_MathML_112.jpg$ .

Example 1.12. Prove the identity $tema7_EN_files\tema7_EN_MathML_113.jpg$ .

Hint: Let $tema7_EN_files\tema7_EN_MathML_114.jpg$ .

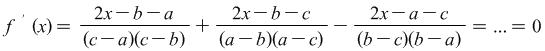
$tema7_EN_files\tema7_EN_MathML_115.jpg$

Consequently $tema7_EN_files\tema7_EN_MathML_116.jpg$ . When $tema7_EN_files\tema7_EN_MathML_117.jpg$

For individual work

Exercise 1.13. Prove the identity $tema7_EN_files\tema7_EN_MathML_118.jpg$ for every x, y.

Exercise 1.14. Prove the identity $tema7_EN_files\tema7_EN_MathML_119.jpg$ for every x,y.

Exercise 1.15. Prove the identity $tema7_EN_files\tema7_EN_MathML_120.jpg$ for every x, y, z.

Exercise 1.16. Prove the identity $tema7_EN_files\tema7_EN_MathML_121.jpg$ for every x, y, z.

Exercise 1.17. Prove the identity $tema7_EN_files\tema7_EN_MathML_122.jpg$ $tema7_EN_files\tema7_EN_MathML_123.jpg$ for every a, b, x, y, z.

Exercise 1.18. Prove the identity $tema7_EN_files\tema7_EN_MathML_124.jpg$ for every a, b, c.

Exercise 1.19. Prove the identity $tema7_EN_files\tema7_EN_MathML_125.jpg$ for every a, b, c.

2 Proving trigonometric identities

The algorithm offered can be used for proving trigonometric identities. It has to be mentioned, though, that the derivatives of differences which result from subtraction of trigonometric expressions, rather than the identities themselves which have to be proven. This means that more complex transformations have to be carried out to prove that $tema7_EN_files\tema7_EN_MathML_126.jpg$ . This is why we will only illustrate this application with a few examples, and the rest will remain to be done individually.

Prove the identities:

Example 2.1. Prove the identity $tema7_EN_files\tema7_EN_MathML_127.jpg$ for every x.

Solution: Let $tema7_EN_files\tema7_EN_MathML_128.jpg$

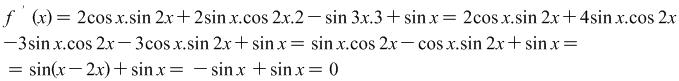
$tema7_EN_files\tema7_EN_MathML_129.jpg$

Then $tema7_EN_files\tema7_EN_MathML_130.jpg$ . When $tema7_EN_files\tema7_EN_MathML_131.jpg$ the result is that $tema7_EN_files\tema7_EN_MathML_132.jpg$

$tema7_EN_files\tema7_EN_MathML_133.jpg$ . Consequently $tema7_EN_files\tema7_EN_MathML_134.jpg$

Example 2.2. Prove the identity $tema7_EN_files\tema7_EN_MathML_135.jpg$ for every x.

Solution: Let $tema7_EN_files\tema7_EN_MathML_136.jpg$

$tema7_EN_files\tema7_EN_MathML_137.jpg$

$tema7_EN_files\tema7_EN_MathML_138.jpg$

When $tema7_EN_files\tema7_EN_MathML_139.jpg$ .

Example 2.3. Prove the identity $tema7_EN_files\tema7_EN_MathML_140.jpg$ for every $tema7_EN_files\tema7_EN_MathML_141.jpg$ .

Solution: $tema7_EN_files\tema7_EN_MathML_142.jpg$

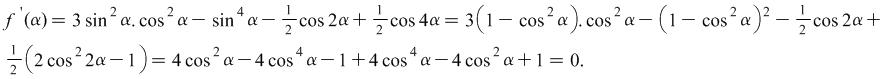
$tema7_EN_files\tema7_EN_MathML_143.jpg$

Consequently $tema7_EN_files\tema7_EN_MathML_144.jpg$ . When $tema7_EN_files\tema7_EN_MathML_145.jpg$ .

Example 2.4. Prove the identity $tema7_EN_files\tema7_EN_MathML_146.jpg$ for every $tema7_EN_files\tema7_EN_MathML_147.jpg$ .

Solution: Let $tema7_EN_files\tema7_EN_MathML_148.jpg$ .

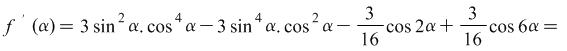
$tema7_EN_files\tema7_EN_MathML_149.jpg$

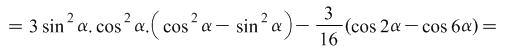
$tema7_EN_files\tema7_EN_MathML_150.jpg$

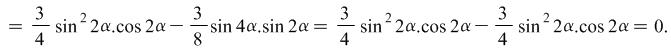
$tema7_EN_files\tema7_EN_MathML_151.jpg$

Consequently $tema7_EN_files\tema7_EN_MathML_152.jpg$ . When $tema7_EN_files\tema7_EN_MathML_153.jpg$

Example 2.5. Prove the identity $tema7_EN_files\tema7_EN_MathML_154.jpg$ for every $tema7_EN_files\tema7_EN_MathML_155.jpg$

Hint: Consider this function: $tema7_EN_files\tema7_EN_MathML_156.jpg$ . Determine that $tema7_EN_files\tema7_EN_MathML_157.jpg$ Establish the constant for $tema7_EN_files\tema7_EN_MathML_158.jpg$

For trigonometric identities with two or more variables we do the following: we introduce the function $tema7_EN_files\tema7_EN_MathML_159.jpg$ , as a function of one of these variables. The remaining are treated as constants. In this case after finding the first derivative of $tema7_EN_files\tema7_EN_MathML_160.jpg$ , many of the summands cease to play a part since their derivatives are zeros. And though some of the problems require a lot of calculation, they are simpler and easier.

Example 2.6. Prove the identity $tema7_EN_files\tema7_EN_MathML_161.jpg$ for every x.

Solution: We assume that $tema7_EN_files\tema7_EN_MathML_162.jpg$ is a constant and consider the function

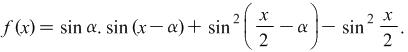
$tema7_EN_files\tema7_EN_MathML_163.jpg$

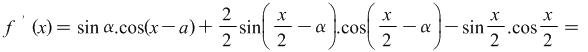
$tema7_EN_files\tema7_EN_MathML_164.jpg$

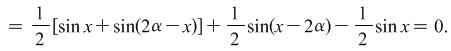
$tema7_EN_files\tema7_EN_MathML_165.jpg$

Consequently $tema7_EN_files\tema7_EN_MathML_166.jpg$ . Let $tema7_EN_files\tema7_EN_MathML_167.jpg$ . Then $tema7_EN_files\tema7_EN_MathML_168.jpg$ .

Example 2.7. Prove the identity $tema7_EN_files\tema7_EN_MathML_169.jpg$ for every $tema7_EN_files\tema7_EN_MathML_170.jpg$ .

Solution: Let's assume that $tema7_EN_files\tema7_EN_MathML_171.jpg$ is a constant. Then

$tema7_EN_files\tema7_EN_MathML_172.jpg$

$tema7_EN_files\tema7_EN_MathML_173.jpg$

$tema7_EN_files\tema7_EN_MathML_174.jpg$

$tema7_EN_files\tema7_EN_MathML_175.jpg$

When $tema7_EN_files\tema7_EN_MathML_176.jpg$ , we determine that $tema7_EN_files\tema7_EN_MathML_177.jpg$ .

Example 2.8. Prove the identity $tema7_EN_files\tema7_EN_MathML_178.jpg$ for every $tema7_EN_files\tema7_EN_MathML_179.jpg$

Solution: $tema7_EN_files\tema7_EN_MathML_180.jpg$ .

$tema7_EN_files\tema7_EN_MathML_181.jpg$

When $tema7_EN_files\tema7_EN_MathML_182.jpg$

The basic theorem can be used for proving conditional trigonometric identities.

Example 2.9. Prove the identity $tema7_EN_files\tema7_EN_MathML_183.jpg$ , if $tema7_EN_files\tema7_EN_MathML_184.jpg$ .

Solution: $tema7_EN_files\tema7_EN_MathML_185.jpg$ ,

$tema7_EN_files\tema7_EN_MathML_186.jpg$

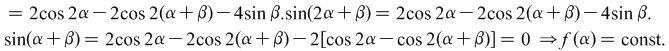
$tema7_EN_files\tema7_EN_MathML_187.jpg$

When $tema7_EN_files\tema7_EN_MathML_188.jpg$ .

Example 2.10. Prove the identity $tema7_EN_files\tema7_EN_MathML_189.jpg$ , if $tema7_EN_files\tema7_EN_MathML_190.jpg$ .

Solution: $tema7_EN_files\tema7_EN_MathML_191.jpg$

$tema7_EN_files\tema7_EN_MathML_192.jpg$

$tema7_EN_files\tema7_EN_MathML_193.jpg$

When $tema7_EN_files\tema7_EN_MathML_194.jpg$ .

Example 2.11. Prove the identity $tema7_EN_files\tema7_EN_MathML_195.jpg$ if $tema7_EN_files\tema7_EN_MathML_196.jpg$ .

Solution: $tema7_EN_files\tema7_EN_MathML_197.jpg$

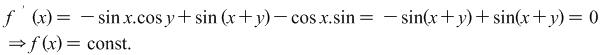
$tema7_EN_files\tema7_EN_MathML_198.jpg$

When $tema7_EN_files\tema7_EN_MathML_199.jpg$ . Consequently $tema7_EN_files\tema7_EN_MathML_200.jpg$ .

Example 2.12. Prove the identity $tema7_EN_files\tema7_EN_MathML_201.jpg$ $tema7_EN_files\tema7_EN_MathML_202.jpg$ , if $tema7_EN_files\tema7_EN_MathML_203.jpg$ , $tema7_EN_files\tema7_EN_MathML_204.jpg$ .

Hint: Consider $tema7_EN_files\tema7_EN_MathML_205.jpg$ . Find $tema7_EN_files\tema7_EN_MathML_206.jpg$ and $tema7_EN_files\tema7_EN_MathML_207.jpg$ .

Example 2.13. Prove the identity $tema7_EN_files\tema7_EN_MathML_208.jpg$ , if $tema7_EN_files\tema7_EN_MathML_209.jpg$ .

Hint: Let $tema7_EN_files\tema7_EN_MathML_210.jpg$

Determine $tema7_EN_files\tema7_EN_MathML_211.jpg$ and find $tema7_EN_files\tema7_EN_MathML_212.jpg$ when $tema7_EN_files\tema7_EN_MathML_213.jpg$ .

For individual work

Prove the following identities:

Problem 2.14. $tema7_EN_files\tema7_EN_MathML_214.jpg$ for every $tema7_EN_files\tema7_EN_MathML_215.jpg$

Problem 2.15. $tema7_EN_files\tema7_EN_MathML_216.jpg$ for every $tema7_EN_files\tema7_EN_MathML_217.jpg$

Problem 2.16. $tema7_EN_files\tema7_EN_MathML_218.jpg$

Problem 2.17. $tema7_EN_files\tema7_EN_MathML_219.jpg$

Problem 2.18. $tema7_EN_files\tema7_EN_MathML_220.jpg$

Problem 2.19. $tema7_EN_files\tema7_EN_MathML_221.jpg$

Problem 2.20. $tema7_EN_files\tema7_EN_MathML_222.jpg$

Problem 2.21. $tema7_EN_files\tema7_EN_MathML_223.jpg$

Problem 2.22. $tema7_EN_files\tema7_EN_MathML_224.jpg$

Problem 2.23. $tema7_EN_files\tema7_EN_MathML_225.jpg$ , if $tema7_EN_files\tema7_EN_MathML_226.jpg$

Problem 2.24. $tema7_EN_files\tema7_EN_MathML_227.jpg$ , if $tema7_EN_files\tema7_EN_MathML_228.jpg$

Problem 2.25. $tema7_EN_files\tema7_EN_MathML_229.jpg$ , if $tema7_EN_files\tema7_EN_MathML_230.jpg$

Problem 2.26. $tema7_EN_files\tema7_EN_MathML_231.jpg$ , if $tema7_EN_files\tema7_EN_MathML_232.jpg$ .

By Ilia Makrelov, Plovdiv university, ilmak@uni-plovdiv.bg