Function limits
Aim:
If any function isn't defined for some value of the argument ![]() , then it is natural to inquire what is the behavior of this function when argument
, then it is natural to inquire what is the behavior of this function when argument ![]() assumes values infinitely attend to
assumes values infinitely attend to![]() . For this reason it is necessary to set up and adopt the concept of a limit. The other aim is to form skills for finding the limit of a function.
. For this reason it is necessary to set up and adopt the concept of a limit. The other aim is to form skills for finding the limit of a function.
Application:
Knowledge and skills to find limits of functions leads to:
1. More precise and exhaustive constructions of function graphcs.
2. Capability to find independently the derivative of a function.
Presentation structure:
1. Why is the concept of function limit studied.
2. Rules for finding limits. Examples.
3. Limits of some of the basic functions. Illustrations.
4. Several examples with solutions.
5. Examples for individual work.
The answer to this question isn't simple that is why we begin with several examples. Let us examine the function ![]() It is evident that this function isn't defined at
It is evident that this function isn't defined at ![]() . Then let us consider what is the behavior of the function when argument
. Then let us consider what is the behavior of the function when argument ![]() takes values infinitely close to the point
takes values infinitely close to the point ![]() The proximity with this point has two aspects: left proximity (marked using the symbol "1-0") and right proximity (marked with the symbol "1+0").
The proximity with this point has two aspects: left proximity (marked using the symbol "1-0") and right proximity (marked with the symbol "1+0").
Let there be given a different function ![]() , which is defined for every
, which is defined for every![]() . The important thing is to know what the behavior of this function is when
. The important thing is to know what the behavior of this function is when ![]() and
and ![]() . But should we encounter a function
. But should we encounter a function ![]() , which is defined for
, which is defined for ![]() , then we would have to be aware what values the given function would approach when
, then we would have to be aware what values the given function would approach when ![]() (to the right of
(to the right of ![]() ) and
) and ![]() (to the left of
(to the left of ![]() ).
).
Everything mentioned up to this point suggests that there is the need to bring in the concept of limit of functionwhen argument ![]() approaches some point
approaches some point ![]() . The symbol used is
. The symbol used is
![]() (
(![]() is read as limit).
is read as limit).
The above written means that the number ![]() is the limit of the function
is the limit of the function ![]() , when
, when ![]() (to the left of right of
(to the left of right of ![]() ). The value for
). The value for ![]() can be either
can be either ![]() or
or ![]() . The same is also true for
. The same is also true for ![]()
Example 1.1. Find the limit of the function ![]() , when
, when ![]() (to the left and right) and the limit of the function
(to the left and right) and the limit of the function ![]() , when
, when ![]() (to the right
(to the right ![]() and to the left
and to the left ![]() )
)
Solution:

|

|
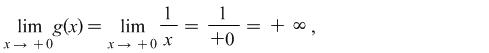
|
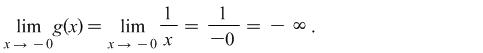
|
Comment: Do not take symbols ![]() or
or ![]() as zero division, but as division by an infinitely small positive
as zero division, but as division by an infinitely small positive ![]() or negative
or negative ![]() number.
number.
Example 1.2. Find the limits of the functions ![]() and
and ![]() , when
, when ![]() .
.
Solution:
![]()


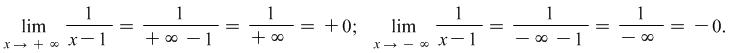
Comment: Symbols ![]() or
or ![]() take as division by an infinitely big positive
take as division by an infinitely big positive ![]() or negative
or negative ![]() number.
number.
It isn't hard to memorize the following proportions for future use:
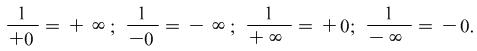
|
For illustration in the next figure we will give you the limits of the functions ![]() and
and ![]()
|
|
| Figure 1 |
|
|
| Figure 2 |
If the function ![]() is defined and continuous in the interval
is defined and continuous in the interval ![]() , then for every point
, then for every point ![]() belonging to this interval it can be written down that
belonging to this interval it can be written down that
|
|
(1.1) |
or more figuratively put, if after the substitution of ![]() with
with ![]() the result is a finite number then that is the sought limit. However this is unlikely to happen to you in a serious exam. You would be required to do something more. You will see later on.
the result is a finite number then that is the sought limit. However this is unlikely to happen to you in a serious exam. You would be required to do something more. You will see later on.
Example 1.3. Find the limits of the function ![]() when
when ![]() and
and ![]() , and the limit of the function
, and the limit of the function ![]() when
when ![]() .
.
Solution: Here formula (1.1) can be used for both functions:
|
|
|
|

|
|
|
(2.1) |
|
|
(2.2) |
In particular ![]()

|
(2.3) |

|
(2.4) |
|
|
(2.5) |
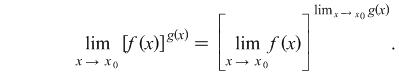
|
(2.6) |
We continue by examining an interesting example.
Example 2.1. Find the limit of the function ![]() when
when ![]() .
.
Solution: Here we apply the rules (2.1), (2.2) and (2.3):
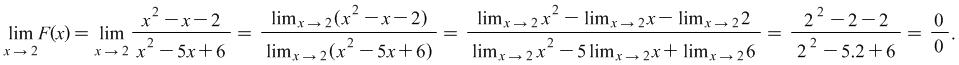
|
The result is the so called indefinite form of the kind ![]() . This means that we still can't determine the limit of the given function.
. This means that we still can't determine the limit of the given function.
Now we will apply a different technique to this example:
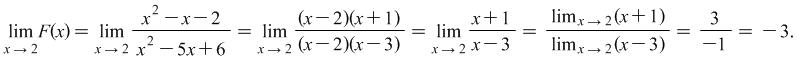
|
Except the shown indefiniteness there are other indefinite types
|
|
In such cases transformations are made in the analytical expression of the function and rules for limit seeking are only then applied.
Such examples should be expected at a serious exam.
Definition 2.2. Finding a limit in case of indefiniteness when such a limit exists is called indefiniteness expansion.
A useful rule
If we have to determine the limit of a function of the form
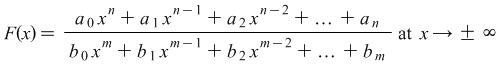
|
then its best that in the numerator and in the denominator we put as multiplier before brackets the highest exponent of ![]() . In that case the given function
. In that case the given function ![]() would look like this
would look like this
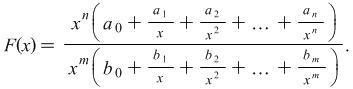
|
Example 2.3. When ![]() find the limits of the functions
find the limits of the functions

|
Solution:
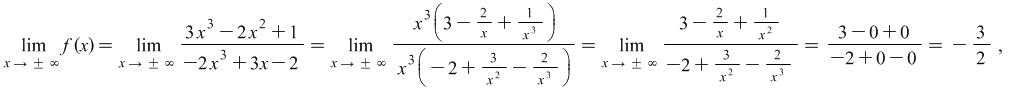
|
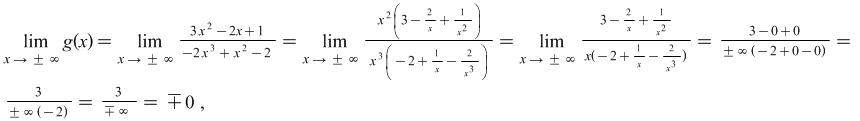
|

|
![]()
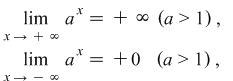
|
(3.1) |
|
|
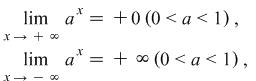
|
(3.2) |
|
|
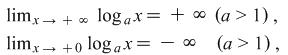
|
(3.3) |
|
|

|
(3.4) |
|
|
In particular
|
|
|
|
Example 4.1. Find the limit 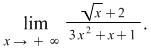
Solution: After substituting ![]() with the limit value of
with the limit value of ![]() we get an indefiniteness of the type
we get an indefiniteness of the type ![]() To cope with the indefiniteness we put as a multiplier before brackets the highest exponent of
To cope with the indefiniteness we put as a multiplier before brackets the highest exponent of ![]() both in the nominator and the denominator:
both in the nominator and the denominator:
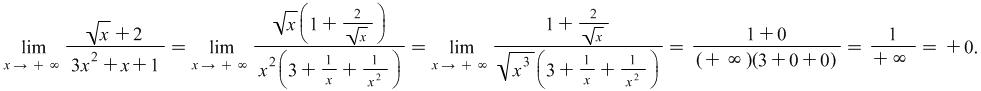
|
Example 4.2. Find the limit ![]()
Solution: Since ![]() we have an indefiniteness of the type
we have an indefiniteness of the type ![]() . (Sometimes instead of
. (Sometimes instead of ![]() or
or ![]() is used
is used ![]() or
or ![]() )
)
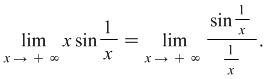
|
We replace ![]() . Then for
. Then for ![]() we have
we have ![]() (or
(or ![]() ). Consequently
). Consequently 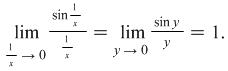
Example 4.3. Find the limit ![]()
Solution: Here the indefiniteness is of the kind ![]() , because
, because ![]() We have
We have
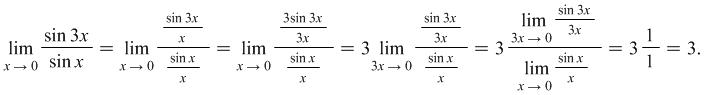
|
Example 4.4. Find the limit 
Solution: After substituting ![]() with the limit value
with the limit value ![]() the result is an indefiniteness of the type
the result is an indefiniteness of the type ![]() . We will try to expand it:
. We will try to expand it:
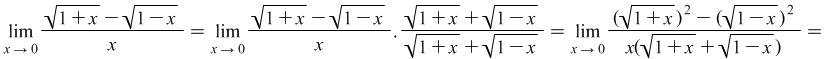
|
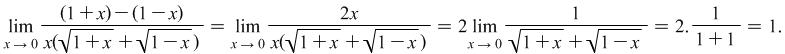
|
Example 4.5. Find the limit 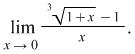
Solution: Again the indefiniteness at hand is of the type ![]() . We will use the formula
. We will use the formula ![]()
If we replace ![]() and
and ![]() the formula above will look like this
the formula above will look like this
|
|
Consequently
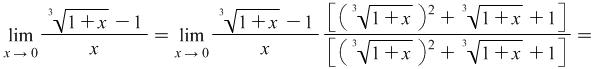
|
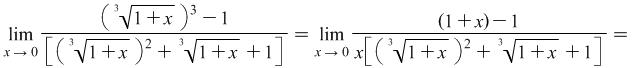
|
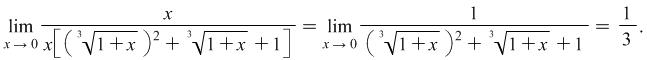
|
Example 4.6. Find the limit 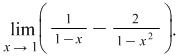
Solution After substituting ![]() with
with ![]() or
or ![]() the result is respectively an indefiniteness of the type
the result is respectively an indefiniteness of the type ![]() or
or ![]() .
.
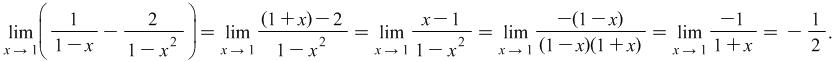
|
Example 4.7. Find the limit 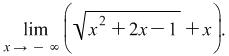
Solution: The indefiniteness of the example is of the type ![]() We have
We have
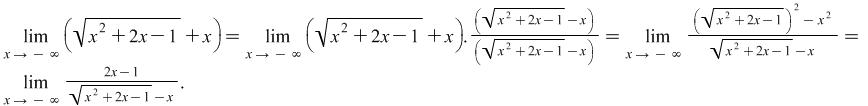
|
After the transformations the indefiniteness is still ![]() . Probably gained experience tells you that both in nominator and denominator we need to put before brackets as a multiplier the respective highest exponent of
. Probably gained experience tells you that both in nominator and denominator we need to put before brackets as a multiplier the respective highest exponent of ![]() :
:

|
Example 4.8. Find the limit ![]()
Solution: We need to use the formula ![]() Then
Then ![]() .
.
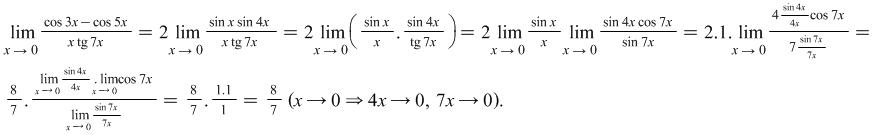
|
Example 4.9. Find the limit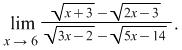
Solution: After the substitution of ![]() with the limit value (in the case
with the limit value (in the case ![]() ) the result is an indefiniteness of the type
) the result is an indefiniteness of the type ![]() .
.
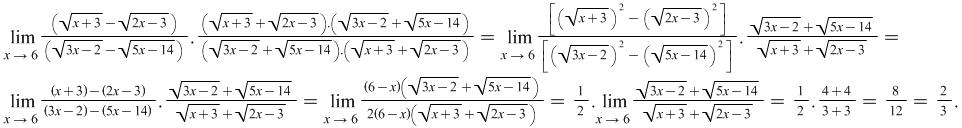
|
Problem 4.10. Below are the graphics of for functions ![]() and
and ![]() .You have to determine what are the limits of the first three functions when
.You have to determine what are the limits of the first three functions when ![]() and the limits of the forth when
and the limits of the forth when ![]()
![]() ,
, ![]() .
.
|
|
|
|
|
|
|
|
Exercise 4.11. Below is the graphics for the function ![]() , which is defined in intervals
, which is defined in intervals ![]() .
.
Try to show what are the limits of the function when ![]() and
and ![]() .
.
|
|
Exercise 4.12. Find the limit  .
.
Answer ![]() .
.
Exercise 4.13. Find the limit ![]() .
.
Answer ![]() .
.
Exercise 4.14. Find the limit ![]()
Answer ![]()
Exercise 4.15. Find the limit 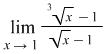 .
.
Answer ![]() .
.
Conclusion If you have in the end understood what has been read up to this point you wouldn't be surprised when you encounter something written down this way ![]() , which means that
, which means that ![]() or
or ![]() , which is the same as
, which is the same as ![]() Interpretation is done analogically for
Interpretation is done analogically for ![]() ,
, ![]() ,
, ![]() etc.
etc.
By Ilia Makrelov, Plovdiv university, ilmak@uni-plovdiv.bg