Solving problems using substitutions
Essense of the method: The given problem is transformed into a new one by changing the region of solutions ![]() into
into ![]() so that every element
so that every element ![]() corresponds to an element
corresponds to an element ![]() and follows a certain rule
and follows a certain rule ![]() . Hence the set of solutions to the problem
. Hence the set of solutions to the problem ![]() is transformed into a set of solutions
is transformed into a set of solutions ![]() by means of
by means of ![]() the sought set
the sought set ![]() for the given problem is found. This correspondence between
for the given problem is found. This correspondence between ![]() , defined by means of
, defined by means of ![]() , is called susbstitution.
, is called susbstitution.
Example 1.1.
Solve the equation ![]()
Solution The equation can be represented in the following way ![]() ( we use the identity
( we use the identity ![]() ). What remains is for the reader to notice that
). What remains is for the reader to notice that ![]() . Then the given equation assumes a more agreeable form
. Then the given equation assumes a more agreeable form ![]()
Obviously we make the substitution ![]() and after that we solve the equation
and after that we solve the equation ![]() . Its roots are
. Its roots are ![]() and
and ![]() . What remains is to solve the quadratic equations
. What remains is to solve the quadratic equations ![]() and
and ![]() and to unite their solutions.
and to unite their solutions.
Example 1.2.
Solve the equation ![]()
Solution
(variant 1) The arithmetic mean of 4,5,6 and 7 is 5.5. We make the substitution ![]() and reduce the equation to the nicer
and reduce the equation to the nicer ![]() , the solution to which is easy to find.
, the solution to which is easy to find.
(variant 2) Multiplying ![]() and
and ![]() the given equation is transformed into
the given equation is transformed into ![]() We have to good possibilities for substitution
We have to good possibilities for substitution ![]() or
or ![]()
Example 1.3.
Solve the equation ![]()
Solution
If you notice that you can represent the equation in the form ![]() then the substitution
then the substitution ![]() will be useful
will be useful![]()
![]()
Example 1.4.
Solve the inequality ![]() .
.
Solution
With a bit more resourcefulness the given inequality will look like this ![]() or
or ![]()
A suitable subsititution is ![]() . Now we will solve the quadratic inequality
. Now we will solve the quadratic inequality ![]()
Going back to the unknown quantity ![]()
![]() it is necessary to solve a double inequality
it is necessary to solve a double inequality ![]() which is the same as the following system
which is the same as the following system 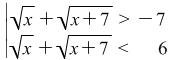 .
.
After finding the solutions to each of the inequalities and then take their intersection you get the answer ![]() .
.
Example 1.5.
Solve the equation ![]()
Hint
If we add to both sides of the expression ![]() (doubled product) we get
(doubled product) we get ![]() or
or ![]()
If you notice that![]()
![]() , then the previous equation will look like this
, then the previous equation will look like this ![]() Of course the substitution is
Of course the substitution is ![]()
Example 1.6.
Solve the equation ![]()
Hint
We replace the equation with its equivalent ![]() The substitution is
The substitution is ![]() .
.
Exercise 1.1. Solve the equation ![]() .
.
Exercise 1.2. Solve the equation ![]() .
.
Exercise 1.3. Solve the equation ![]() .
.
Exercise 1.4. Solve the inequality ![]() .
.
Example 2.1.
Solve the equation ![]() .
.
Solution
(variant 1) A suitable substitution is ![]()
We get the following system of equations 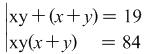 . Let
. Let ![]() and
and ![]() .
.
The system now looks like this 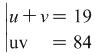 . This way it is pleasing to be looked at as well as to be solved.
. This way it is pleasing to be looked at as well as to be solved.
(variant 2) We make the substitutions directly ![]() и
и ![]() and get the system
and get the system 
After solving it the solutions to the given equation are found through the equations ![]() and
and ![]()
Example 2.2.
Solve the equation ![]() and
and ![]() .
.
Solution Let ![]() and
and ![]() . Then the equation will look like this
. Then the equation will look like this ![]() The second equation for
The second equation for ![]() and
and ![]() we will get when we multiply
we will get when we multiply ![]() and
and ![]() respectively with
respectively with ![]() and
and ![]() and then add them together. The result is
and then add them together. The result is ![]() , i.e. the system is
, i.e. the system is 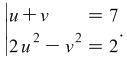 After determining
After determining ![]() and
and ![]() and going back to the substitutions it is easy to find that
and going back to the substitutions it is easy to find that ![]() .
.
Example 2.3.
Solve the equation ![]() .
.
Solution Let ![]() and
and ![]() Then the given equation will look like this
Then the given equation will look like this ![]() . The second equation for
. The second equation for ![]() and
and ![]() we will get by adding together term by term
we will get by adding together term by term ![]() and
and ![]() , i.e.
, i.e.![]() . The result is the following system
. The result is the following system  whose solutions are
whose solutions are ![]() . Going back to the substitutions we find that
. Going back to the substitutions we find that ![]() .
.
Example 2.4.
Solve the equation ![]() .
.
Hint
We make the substitutions![]() and
and ![]() and solve the following system
and solve the following system 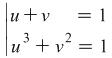 .
.
Answer
![]() .
.
Exercise 2.1. Solve the equation ![]() .
.
Exercise 2.2. Solve the equation ![]() .
.
Exercise 2.3. Solve the equation ![]() .
.
Example 3.1.
Solve the system 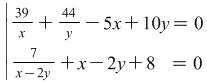 .
.
Solution The system can be written down in the form 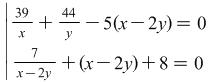 .
.
A suitable substitution is ![]() . Then the second equation of the system will look like this
. Then the second equation of the system will look like this ![]() . Later on the set of solutions of the system becomes a union of the sets of solutions of the systems
. Later on the set of solutions of the system becomes a union of the sets of solutions of the systems 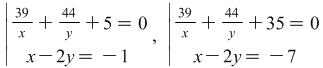 :
:
Example 3.2.
Solve the system 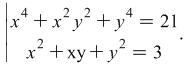
Solution Notice that the left sides of both equations are symmetric expressions in regard to ![]() and
and ![]() . To solve such systems substitutions
. To solve such systems substitutions![]() and
and ![]() are used. Before that we will replace the system with its equivalent system
are used. Before that we will replace the system with its equivalent system 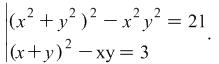 (We bring to notice that
(We bring to notice that![]() and
and ![]() ).
).
We make the substitutions ![]() and
and ![]() and solve the system
and solve the system 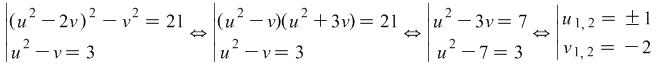
In the end we have to solve the systems 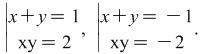 Notice that if
Notice that if ![]() and
and ![]() are the respective sets of solutions to the last two systems, then the solution of the given system is the set
are the respective sets of solutions to the last two systems, then the solution of the given system is the set ![]() .
.
Exercise 3.1. Solve the system 
Hint
We replace ![]() and
and ![]() and the system is reduced to the following system
and the system is reduced to the following system 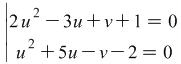 . If you add together the equations of the new system you will get a quadratic equation
. If you add together the equations of the new system you will get a quadratic equation![]() .
.
Exercise 3.2. Solve the system 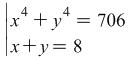 .
.
Hint Again replace ![]() and
and ![]() and keep in mind that
and keep in mind that ![]() .
.
By Rumiana Mavrova and Ilia Makrelov, Plovdiv university, rummav@pu.acad.bg , ilmak@pu.acad.bg