Fourth-order Runge-Kutta Method for systems of ordinary differential equations using Mathematica
Аnotation
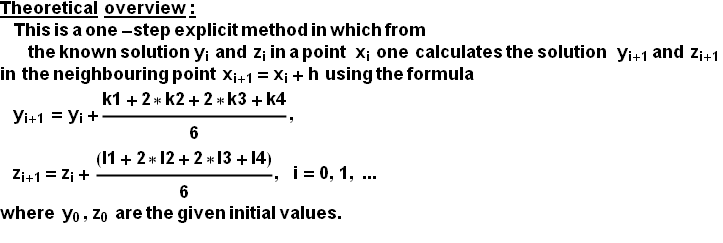
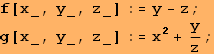
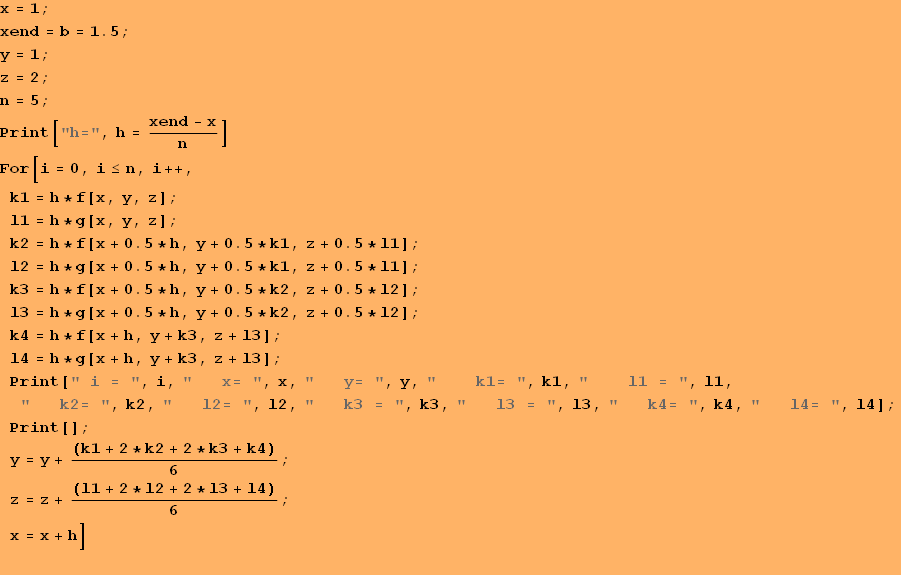
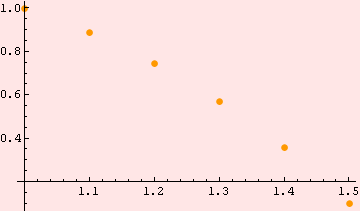
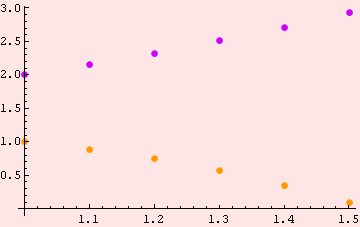
| 1 | 1. | 2. |
| 1.1 | 0.886873 | 2.15592 |
| 1.2 | 0.744792 | 2.32486 |
| 1.3 | 0.569252 | 2.50858 |
| 1.4 | 0.355089 | 2.70883 |
| 1.5 | 0.0964108 | 2.92739 |
Conclusion: The solution derived using the Runge-Kutta method O(
) is in the form of a table of the functions y(x) and z(x), shown in the second and third columns of the table above, respectively. Since the local apriori error of the method is O(
) (or global error is O(
) ) and here h=0.1, then these solutions must be rounded to three symbols after the decimal point.
Graphics of the solution
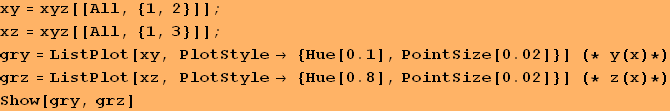
| Created by Wolfram Mathematica 6.0 (22 September 2008) |  |