Two-order Runge-Kutta Method using Mathematica
![]()
Аnotation
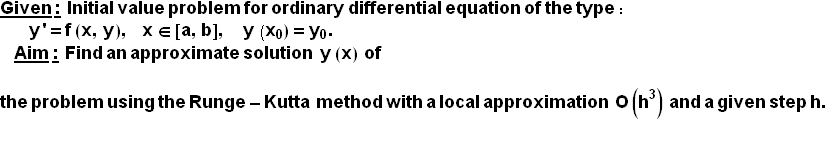

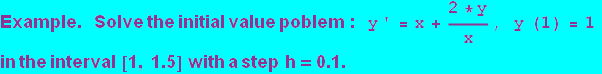
![]()
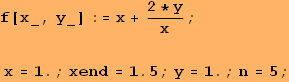
![]()
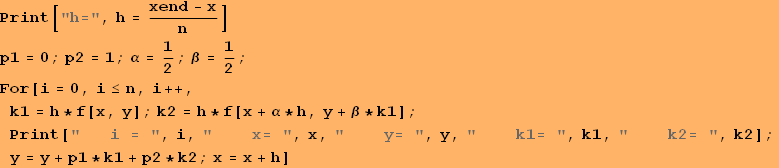
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
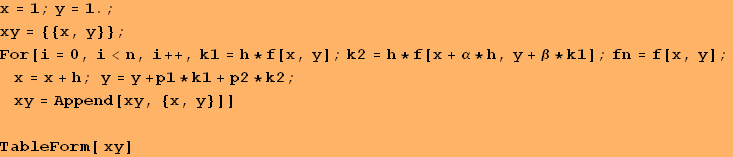
| 1 | 1. |
| 1.1 | 1.32405 |
| 1.2 | 1.69982 |
| 1.3 | 2.12905 |
| 1.4 | 2.61336 |
| 1.5 | 3.15422 |
Conclusion: The solution derived using the Runge-Kutta method O(![]() ) is in the form of a table of the variable function y(x), shown in the second column of the table above. Since the local apriori error of the method is O(
) is in the form of a table of the variable function y(x), shown in the second column of the table above. Since the local apriori error of the method is O(![]() ) (or global error is O(
) (or global error is O(![]() ) ) and here h=0.1, then these solutions must be rounded to three symbols after the decimal point.
) ) and here h=0.1, then these solutions must be rounded to three symbols after the decimal point.
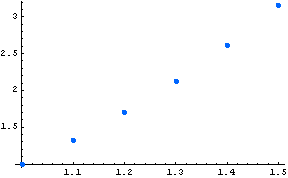
Graphic of the solution
![]()
![]()
| Created by Wolfram Mathematica 6.0 (22 September 2008) |