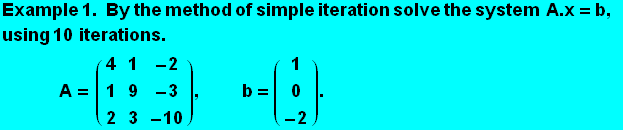
Examples of simple iteration and Seidel methods
for solving linear systems of equations by using Mathematica code

By Snezhana Gocheva-Ilieva, snow@pu.acad.bg

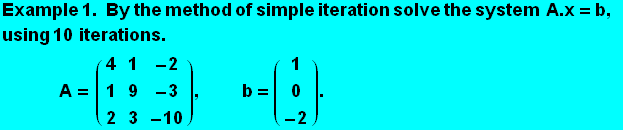
RowBox[{StyleBox[RowBox[{RowBox[{Example, , 1.,    , By, , the, , method, , ... 3 -10 -2

Solution:
We introduce:

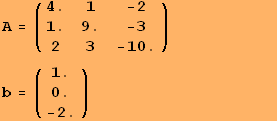
A = (4. 1 -2 )            &nb ... p;    1. 9. -3 2 3 -10. b = (1. ) 0. -2.

RowBox[{{, RowBox[{RowBox[{{, RowBox[{4., ,, 1, ,, -2}], }}], ,, RowBox[{{, RowBox[{1., ,, 9., ,, -3}], }}], ,, RowBox[{{, RowBox[{2, ,, 3, ,, RowBox[{-, 10.}]}], }}]}], }}]

RowBox[{{, RowBox[{RowBox[{{, 1., }}], ,, RowBox[{{, 0., }}], ,, RowBox[{{, RowBox[{-, 2.}], }}]}], }}]

First we could reduce the system in the form, appropriate for iteration:

n = 3 ;       c = {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}} ; d = {0, 0, ... ;    , d[[i]] = b[[i]]/z, ;}]}], , , ]}] MatrixForm[c] MatrixForm[d]

( 0.` -0.25` 0.5` ) ... 0.3333333333333333` 0.2` 0.30000000000000004` 0.`

( 0.25` ) 0.` 0.2`

Then calculate of the first matrix norm of matrix C:

p1 = Underoverscript[∑, j = 1, arg3] Abs[ c[[1, j]] ] p2 = Underoverscript[∑, j = ... first norm of matrix c is =  Max of the sums of absolute values per row =", mnor1]

0.75

0.444444

0.5

RowBox[{ The first norm of matrix c is =  Max of the sums of absolute values per row =, , 0.75}]

As the norm is lower than 1 we expect the convergence of the iteration process.  The following code performs the simple iteration method procedure:

m = 10 ; k = 0 ; x = {0, 0, 0} ; Print[" Number of iteration = ", k, " &nb ... = xnovo] Print[" Approximate solution by the simple iteration method is= ", x]

Number of iteration = 0   x =  {0, 0, 0}

RowBox[{ Number of iteration = , , 1, ,    x = , , RowBox[{{, RowBox[{RowBox[{{, 0.25, }}], ,, RowBox[{{, 0., }}], ,, RowBox[{{, 0.2, }}]}], }}]}]

RowBox[{ Number of iteration = , , 2, ,    x = , , RowB ... x[{{, RowBox[{RowBox[{{, 0.35, }}], ,, RowBox[{{, 0.0388889, }}], ,, RowBox[{{, 0.25, }}]}], }}]}]

RowBox[{ Number of iteration = , , 3, ,    x = , , RowB ... wBox[{RowBox[{{, 0.365278, }}], ,, RowBox[{{, 0.0444444, }}], ,, RowBox[{{, 0.281667, }}]}], }}]}]

RowBox[{ Number of iteration = , , 4, ,    x = , , RowB ... wBox[{RowBox[{{, 0.379722, }}], ,, RowBox[{{, 0.0533025, }}], ,, RowBox[{{, 0.286389, }}]}], }}]}]

RowBox[{ Number of iteration = , , 5, ,    x = , , RowB ... wBox[{RowBox[{{, 0.379869, }}], ,, RowBox[{{, 0.0532716, }}], ,, RowBox[{{, 0.291935, }}]}], }}]}]

RowBox[{ Number of iteration = , , 6, ,    x = , , RowB ... owBox[{RowBox[{{, 0.38265, }}], ,, RowBox[{{, 0.0551041, }}], ,, RowBox[{{, 0.291955, }}]}], }}]}]

RowBox[{ Number of iteration = , , 7, ,    x = , , RowB ... wBox[{RowBox[{{, 0.382202, }}], ,, RowBox[{{, 0.0548018, }}], ,, RowBox[{{, 0.293061, }}]}], }}]}]

RowBox[{ Number of iteration = , , 8, ,    x = , , RowB ... owBox[{RowBox[{{, 0.38283, }}], ,, RowBox[{{, 0.0552202, }}], ,, RowBox[{{, 0.292881, }}]}], }}]}]

RowBox[{ Number of iteration = , , 9, ,    x = , , RowB ... wBox[{RowBox[{{, 0.382635, }}], ,, RowBox[{{, 0.0550903, }}], ,, RowBox[{{, 0.293132, }}]}], }}]}]

RowBox[{ Number of iteration = , , 10, ,    x = , , Row ... wBox[{RowBox[{{, 0.382793, }}], ,, RowBox[{{, 0.0551957, }}], ,, RowBox[{{, 0.293054, }}]}], }}]}]

RowBox[{ Approximate solution by the simple iteration method is= , , RowBox[{{, RowBox[{RowBox[{{, 0.382793, }}], ,, RowBox[{{, 0.0551957, }}], ,, RowBox[{{, 0.293054, }}]}], }}]}]

Verification by substituting the obtained x into the initial system of equations:

A . x - b

RowBox[{{, RowBox[{RowBox[{{, 0.000261252, }}], ,, RowBox[{{, 0.000391903, }}], ,, RowBox[{{, 0.000632358, }}]}], }}]

Conclusion:  The accuracy of the obtained approximate solution by the method of simple iteration by applying 10 iterations is  0.001.
Answer:  Approximate solution of example 1 with three decimal digits is
                x={0.383, 0.055, 0.293}
                

StyleBox[RowBox[{Example, , 2.,    , By, , the, , Zeidel, , method,  & ...       }], FontFamily -> Arial, FontSize -> 18., FontWeight -> Bold]

Solution:

We apply the code

m = 10 ; k = 0 ; v = {0, 0, 0} ; Print[" Number of iteration = ", k, " &nb ... bsp;v = ", v] ;  ] Print[" Approximate solution by Zeidel method is= ", v]

Number of iteration = 0   v =  {0, 0, 0}

RowBox[{ Number of iteration = , , 1, ,    v = , , RowBox[{{, RowBox[{0.25, ,, RowBox[{-, 0.0277778}], ,, 0.241667}], }}]}]

RowBox[{ Number of iteration = , , 2, ,    v = , , RowBox[{{, RowBox[{0.377778, ,, 0.0385802, ,, 0.28713}], }}]}]

RowBox[{ Number of iteration = , , 3, ,    v = , , RowBox[{{, RowBox[{0.38392, ,, 0.0530521, ,, 0.2927}], }}]}]

RowBox[{ Number of iteration = , , 4, ,    v = , , RowBox[{{, RowBox[{0.383087, ,, 0.0550013, ,, 0.293118}], }}]}]

RowBox[{ Number of iteration = , , 5, ,    v = , , RowBox[{{, RowBox[{0.382809, ,, 0.0551716, ,, 0.293113}], }}]}]

RowBox[{ Number of iteration = , , 6, ,    v = , , RowBox[{{, RowBox[{0.382764, ,, 0.0551751, ,, 0.293105}], }}]}]

RowBox[{ Number of iteration = , , 7, ,    v = , , RowBox[{{, RowBox[{0.382759, ,, 0.055173, ,, 0.293104}], }}]}]

RowBox[{ Number of iteration = , , 8, ,    v = , , RowBox[{{, RowBox[{0.382759, ,, 0.0551725, ,, 0.293103}], }}]}]

RowBox[{ Number of iteration = , , 9, ,    v = , , RowBox[{{, RowBox[{0.382759, ,, 0.0551724, ,, 0.293103}], }}]}]

RowBox[{ Number of iteration = , , 10, ,    v = , , RowBox[{{, RowBox[{0.382759, ,, 0.0551724, ,, 0.293103}], }}]}]

RowBox[{ Approximate solution by Zeidel method is= , , RowBox[{{, RowBox[{0.382759, ,, 0.0551724, ,, 0.293103}], }}]}]

Verification by substituting the obtained x=v into the initial system of equations:

A . v - b

RowBox[{{, RowBox[{RowBox[{{, RowBox[{-, 6.40224*10^-9}], }}], ,, RowBox[{{, 3.08924*10^-10, }}], ,, RowBox[{{, 0., }}]}], }}]

Conclusion:  The accuracy of the obtained approximate solution by the Zeidel  method after 10 iterations is  0.000000001.
Answer:  Approximate solution of example 2 with six decimal digits is
                x={0.382759, 0.0551724, 0.293103}.
                

Created by Mathematica  (May 8, 2008)