Free-Form Deformations of Solid Cells

1. Introduction

Solid cell T is a non-empty subset of the projectively extended Euclidean space over the real numbers _¥E³ that is the image of a simply connected region W = <0, 1> Ì R³ under a locally homeomorphic mapping analytically represented by the point function

s(uⁱ) = (x(uⁱ), y(uⁱ), z(uⁱ), h(uⁱ)), for i = 1, 2, 3.

Separate components x(uⁱ), y(uⁱ), z(uⁱ), h(uⁱ) are homogeneous co-ordinate functions in three real variables differentiable on W, h(uⁱ) = 0 for ideal solid cell points, for real points h(uⁱ) = 1 in the normalised form. Numbers (a, b, c) Î W are curvilinear co-ordinates of point P(a, b, c) located in solid cell. Net of iso-parametric surface patches in the solid cell is composed from three systems of iso-parametric surface patches, which are determined for one constant value of parameters u¹ = a, or u² = b, or u³ = c, and they are represented by point functions in two variables s(u¹, u², c), s(a, u², u³), s(u¹, b, u³), for (a, b, c) Î W. All three iso-parametric surface patches meet in the solid cell point P = s(a, b, c), and any two of them intersect in the solid cell iso-parametric curve segment. Iso-parametric curve segments, all passing through their common regular point P = s(a, b, c) are represented by the point functions in one variable s(u¹, b, c), s(a, u², c), s(a, b, u³), while (u¹, u², u³) Î W.

Point P = s(a, b, c), for (a, b, c) Î W is the regular point of the solid cell, when all three partial derivatives of the solid cell point function with respect to the particular variables

determine linearly independent vectors s_i(a, b, c), i =1, 2, 3, which are tangent vectors to the solid cell iso-parametric curve segments.

In the solid cell regular point P = s(a, b, c), (a, b, c) Î W, the tangent trihedron is uniquely determined and it describes solid intrinsic geometric properties. Vertex of the tangent trihedron is the regular point P. Edges are semi-lines determined by the point P and three direction vectors s_i(a, b, c), i = 1, 2, 3 in the tangent vectors to the solid cell iso-parametric curve segments located in the point P. Faces of the trihedron are parts of three tangent planes to the solid iso-parametric surface patches sharing the common regular point P (Fig. 1)

t¹² = Ps₁s₂ , t¹³ = Ps₁s₃ ,. t²³ = Ps₂s₃ .

Second mixed partial derivatives of the solid cell point function denoted

determine twist vectors s_ij(a, b, c), i = 1, 2, j = 2, 3, i ¹ j, to the solid cell iso-parametric surface patches in the solid cell regular point P.

The third mixed triple partial derivative of the solid cell point function denoted

determines the solid cell density vector s₁₂₃(a, b, c) in the solid regular point P.

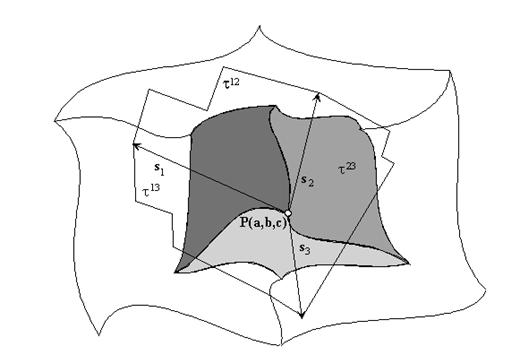
Fig. 1

2. Bèzier solid cells

Approximation Bèzier tri-cubic solid cell is determined by the ordered basic grid of 64 real points in the space. Map of the basic figure is the matrix M_4x4x4 with elements in the homogeneous co-ordinates of points in the basic grid

M_4x4x4 = (^ijkP), i, j, k = 0, 1, 2, 3.

Tri-cubic approximation is determined by Bernstein polynomials for a = 1, 2, 3

Be₀(u_a)=(1 - u_a)³ Be₁(u_a)=3u_a(1 - u_a)² Be₂(u_a)=3u_a²(1 - u_a) Be₃(u_a)=u_a³

and interpolation matrices are in the form

^aI(u_a) = (Be₀(u_a), Be₁(u_a), Be₂(u_a), Be₃(u_a)), a=1, 2, 3.

Modelled Bèzier cell has vertices in the vertices of the basic grid, while no other point of the basic figure is located in the cell. Point function of the cell is in the form

s(u¹, u², u³) = ³I(u³) . (¹I(u¹) . M_4x4x4 . ²I(u²)^T)= ^ijkPBe_i(u¹)Be_j(u²)Be_k(u³), i, j, k = 0, 1, 2, 3.

Density vector s₁₂₃(a, b, c) in the cell arbitrary point P(a, b, c), for a, b, c Î <0, 1> is determined by points of the basic grid and can be calculated from the density function

s₁₂₃(u¹, u², u³) = ³I´(u³).(¹I´(u¹).M_4x4x4.²I´(u²) ^T) = ^ijkPBe_i´(u¹)Be_j´(u²)Be_k´(u³), i, j, k = 0, 1, 2, 3

^aI´(u_a)=(Be₀´(u_a), Be₁´(u_a), Be₂´(u_a), Be₃´(u_a)), a=1, 2, 3

Be₀´(u_a) = -3(1 - u_a)², Be₁´(u_a) = 3(1-u_a )(1 - 3u_a), Be₂´(u_a) = 3u_a (2 - 3u_a), Be₃´(u_a) = 6u_a²

which is the polynomial function of degree two in three variables, where ^ijkP are points of the basic grid, elements of the map M_4x4x4.

Density vectors in the vertices of the Bèzier cell (with parametric coordinates equal to 0 or 1) are determined with respect to the form of the Bernstein polynomials derivatives by 8 interior points of the cell basic grid: vertex, its 3 neighbouring points in the directions of parameters u¹, u², u³, common neighbouring points of these three points in the basic grid, and their common neighbour in the grid. Configuration is illustrated for the vertex ⁰⁰⁰P in Fig. 2.

Considering interior deformations, in which boundary of the cell remains invariant (it means shape of the curve-like edges and surface like facets is preserved), position of points in the grid influencing form of the boundary must be kept unchanged. 8 interior points (one for each vertex) of the basic grid determine interior solid cell geometry and density and they form interior density core, determined as interior density hypercube illustrated in Fig. 3.

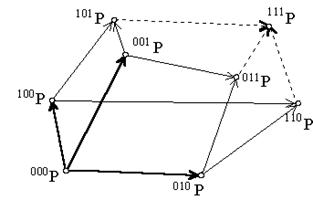
Fig. 2                           Fig. 3

Density core can be deformed arbitrarily (in Fig. 4 vertices of the Bèzier solid cell and vertices of the interior density hypercube are mapped) to create desirable distribution in the net of iso-parametric curve segments and surface patches, and to determine the interior density of the modelled solid cell and its in-homogenity in this way.

Density vectors can be calculated in an arbitrary solid cell regular point for different position of interior density hypercube points, and these can be compared to estimate the results of the deformation. Several illustrations of the in-homogeneous distribution of the degenerated solid cell interior are given in the following, where one face collapses to one edge, while 4 quadruples of the solid cell basic grid points coincide as illustrated in Fig. 5,

ⁱ⁰⁰P = ⁰⁰⁰P, ⁱ⁰¹P = ⁰⁰¹P, ⁱ⁰²P = ⁰⁰²P, ⁱ⁰³P = ⁰⁰³P, for i = 0, 1, 2, 3.

Fig. 4                           Fig.5

In Fig. 6, all vertices of the interior density hypercube are moved within the convex envelope of the Bèzier solid cell basic grid of 64 real points in the matrix M_4x4x4 . Minor deformations of the homogeneous distribution of iso-parametric curve segments in the cell can be reached only, in this way. Illustration in the upper left corner of the Fig. 6 shows the homogeneous position of the iso-parametric net of curve segments in the cell. Deformation in the direction of the parameter u¹ is performed by moving the vertices of the interior density hypercube towards the vertices of the the Bèzier solid cell basic grid (model in upper right corner of the Fig. 6). The first curvature of u³-parametric curve segments determined by point functions s(a, b, u³), u³ Î <0, 1> can be influenced by the singular position of the interior density hypercube vertices in the vertices of the Bèzier solid cell basic grid, as seen on models in the bottom left and right corners of the Fig. 6.

In Fig. 7, vertices of the interior density hypercube are moved outside the convex envelope of the Bèzier solid cell basic grid of 64 real points in the matrix M_4x4x4. Their position is extremely distant from the vertices of the Bèzier solid cell basic grid, but the situation in the upper left corner of the Fig. 7 seems to be very homogeneous, either. This is the result of the symmetric position of the transformed interior density hypercube vertices with respect to the vertices of the deformed Bèzier solid cell. Model in the bottom left corner of the Fig. 7 was created by moving the interior density hypercube vertices extremely far in the direction of the parameter u¹, while in the model in the bottom right corner of the Fig 7 they are located in the similar position but in the direction of the parameter u².

Extreme in-homogeneity of the distribution of iso-parametric curve segments in the cell can be modelled, when the interior density hypercube vertices of the same face are moved in the opposite directions and to the different distances. Interior holes, bubbles and new edges can be created by this deformation, influencing meaningfully the first curvature of the solid cell iso-parametric curve segments with respect to the expecting results of the performed deformation, as shown in Fig. 8. Model in the bottom left corner looks homogeneously either, because of the symmetric position of the interior density hypercube vertices moved outside the Bèzier solid cell basic grid, thought to the extreme distance and in the opposite directions of the separate parameters.

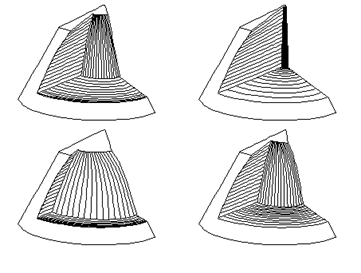
Fig. 6

Fig. 7

Fig. 8