Bezier solid cells

IN-HOMOGENEOUS BÈZIER SOLID CELLS

Basic notions

Basic figure - ordered grid of 64 real points

M_4x4x4 = (^ijkP), i, j, k = 0, 1, 2, 3

Tri-cubic approximation - interpolation matrices

^{aI(u_a) = (Be₀(u_a), Be₁(u_a), Be₂(u_a), Be₃(u_a)), a=1, 2, 3}

determined by Bernstein polynomials for a = 1, 2, 3 , where

Be₀(u_a)=(1 - u_a)³ , Be₁(u_a)=3u_a(1 - u_a)² , Be₂(u_a)=3u_a²(1 - u_a) , Be₃(u_a)=u_a³

Bèzier cell point function on W = <0, 1>²

s(u₁, u₂, u₃) = ³I(u₃) . (¹I(u₁) . M_4x4x4 . ²I(u₂)^T)= ^ijkPBe_i(u₁)Be_j(u₂)Be_k(u₃), i, j, k = 0, 1, 2, 3

Density vector in the cell arbitrary point P(a, b, c), for a, b, c Î á 0, 1ñ

can be calculated from the density function

s₁₂₃(u₁, u₂, u₃) = ³I'(u₃).(¹I'(u₁).M_4x4x4.²I'(u₂)^T) = ^ijkPBe_i'(u₁)Be_j'(u₂)Be_k'(u₃), i, j, k = 0, 1, 2, 3

^{aI'(u_a)=(Be₀'(u_a), Be₁'(u_a), Be₂'(u_a), Be₃'(u_a)), a = 1, 2, 3}

Be₀'(u_a) = -3(1 - u_a)², Be₁'(u_a) = 3(1-u_a )(1 - 3u_a), Be₂'(u_a) = 3u_a (2 - 3u_a), Be₃'(u_a) = 6u_a²

Free-form deformations

Density vectors in the vertices of the Bèzier cell
(with parametric co-ordinates equal to 0 or 1)

are determined (with respect to the form of the Bernstein polynomial derivatives) by

8 interior points of the cell basic grid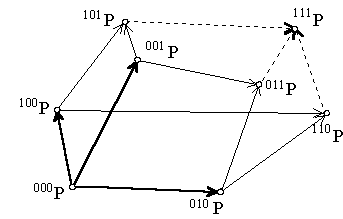

- the entire vertex

- its 3 neighbouring points in the direction of parameter u₁, u₂, and u₃

- common neighbouring points of these 3 points

- their common neighbour in the grid

Considering interior deformations

with invariant boundary of the cell,

position of points in the grid influencing form of the boundary

must be kept unchanged.

8 interior points (one for each vertex) of the basic grid

determine interior solid cell geometry and density

and they form interior density core.

Density core determined by 16 vertices

- the interior density hypercube

can be deformed arbitrarily to create desirable distribution

in the net of the modelled solid cell iso-parametric curve segments and surface patches,

and to determine the interior in-homogenity of the created cell.

Density vectors can be calculated in an arbitrary solid cell regular point

for different position of interior density hypercube vertices,

and these can be compared to estimate the results of the deformation.

Some illustrations of inhomogeneous distribution of the singular solid cell interior

an inhomogeneous Bèzier cube

are given in the following figures.

All inner vertices of the interior density hypercube are moved
within the convex envelope of the Bèzier solid cell basic grid.

A minor deformation of the homogeneous distribution
of iso-parametric curve segments in the cell can be reached only.

The first curvature of iso-parametric curve segments
can be influenced by the singular position of the interior density hypercube vertices
in the vertices of the Bèzier solid cell basic grid.

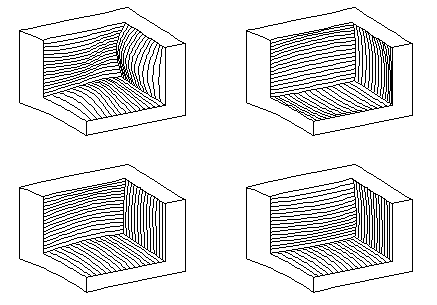
Inner vertices of the interior density hypercube are moved
outside the convex envelope of the Bèzier solid cell basic grid.

Their position can be extremely distant from the vertices of the Bèzier solid cell basic grid,
but the situation in the right bottom corner seems to be very homogeneous, either.

This is the result of the symmetric position of the transformed inner density hypercube vertices
with respect to the vertices of the Bèzier solid cell.

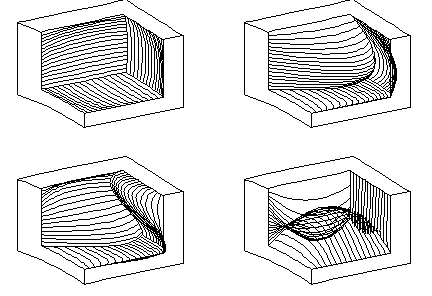
Extreme in-homogeneity of the distribution of iso-parametric curve segments in the cell can be modelled,
when the inner density hypercube vertices of the same facet are moved
in the opposite directions and to the different distances.

Interior holes, bubbles and new edges can be created by this deformation,
influencing meaningfully the first curvature of the solid cell iso-parametric curve segments
with respect to the expecting results of the performed deformation.