
|
| Figure 1: Polar coordinates |
Many scientific and technical applications use polar coordinates in the Euclidean space to solve some of the complex geometric problems.
Let P be the chosen fixed point in the plane. The half-line with the start point P and a determined anti-clockwise revolution about P in the plane form the polar coordinate system . Point P is called the pole - origin of the coordinate system, half-line is the polar axis of the polar coordinate system.

|
| Figure 1: Polar coordinates |
Choosing the measurement unit, any point M in the plane can be attached an ordered pair of real numbers with the clear geometric interpretation illustrated in the Figure 1.
The ordered pair of real numbers form polar coordinates of the point, number is called modul, number or is called the polar angle.
Let the Cartesian coordinate system (O, x, y) and the polar coordinate system be given in the Euclidean plane .
These two coordinate systems are called related, if
and choosing one the other coordinate system is determined uniqely.
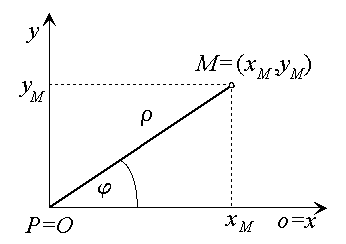
|
| Figure 2: Related coordinate systems |
If are Cartesian coordinates and are polar coordinates of the point M, their relation can be expressed by equations
and because
also by equations
If and thus , the polar angle is not defined by the above equations and the polar coordinates of the point are , where is an arbitrary number.