| ANTOŠ Karel " Problem Solving in High School Mathematics " - from the section: New Trends in Mathematical Education Secondary School Mathematics offers a variety of options to complement the problem solving lesson. This article shows several problem-solving problems that need to be solved through exploration and experimentation. The solution is demonstrated, including proof that is an integral part of these solutions of tasks. Here is how experimentation in problem solving and hypothesis proving can enrich the teaching of mathematics at the secondary level. This enhances the mathematical thinking of students and increases their relationship to mathematics. Solving problem problems increases pupils´ engagement in teaching, thus supporting heuristic approaches to teaching. |
| BALLOVÁ Dominika " Design of Experiments in the Laboratory and the Use of Statistical Methods for Data Analysis " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise In the contribution we present application of Design of Experiments on optimization of chromic salt adsorption on sheep wool. Using four factors involving time and contact manner of the wool with adsorbate solution, the solution concentration and pH as well as ratio of the solution volume to wool mass, all at two levels, optimal conditions for the adsorption experiments were found. Application of those conditions can accelerate research. |
| BAŠTINEC Jaromír " Positive Solutions of Nolinear Discrete Equations " - from the section: Differential Equations, Dynamic Systems and Their Applications 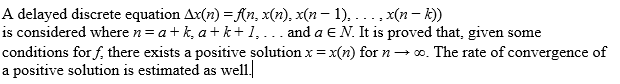 |
| BÁTOROVÁ Martina " Adaptive Scanning of Diverse Heritage Originals like Synagogue Interior, Empty Rare Papers or Herbarium Items from the 19th Century " - from the section: Mathematics and Physics in Contemporary Science and Technique We create the digital twins using the hi-tech CRUSE CS 220ST1100 contactless scanner, providing high precision both in geometry and radiometry. We survey many sharpness functions and we report results of experiments examining how to manually focus the scanner, applying the Fourier transform. We have created the exact representation of interior of a non-existing building, and we also wanted to achieve as true colors as possible of a collection of rare blank handmade papers. Further, we have analyzed requirements for documenting Herbarium data. We discuss selected uncertainty and educational issues within this context. |
| BEREZOVSKII Vladimir " Almost Geodesic Mappings of the Second Type of Spaces With Affine Connection onto Two-Symmetric Spaces " - from the section: Algebra and Geometry and Their Applications In the paper we consider canonical almost geodesic mappings of the second type of spaces with affine connection onto two-symmetric spaces. The main equations for the mappings are obtained as a closed mixed system of PDEs of Cauchy type. We have found the maximum number of essential parameters which the solution of the system depends on. |
| BÍLKOVÁ Diana " Challenge in Modeling the Distribution of Economic Data: LQ-Moments As a More Robust Option " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise LQ-moments represent a certain analogy of classical L-moments, which have been already widely applied in such areas of applied research as construction, meteorology, climatology and hydrology. This paper focuses on the use of LQ-moments in economics. The main aim is to present the use and advantages of this alternative method of estimating the parameters of continuous probability distribution. The calculation of the sample LQ-moments and the construction of the various statistical characteristics of the level, variability, skewness and kurtosis of continuous probability distribution are also an important target of this research. |
| BÍMOVÁ Daniela " Improving Geometric Thinking by Using Planimetric Warm-Ups " - from the section: New Trends in Mathematical Education Geometric thinking either in the two-dimensional plane or in the three-dimensional space is very important for everybody because it’s useful in everyday life on different occasions and it’s also needful in many various professions. For that reason, it’s important to practise geometric thinking starting in childhood. Except practising geometric thinking through typical geometric school problems, geometric thinking can also be improved by the inclusion of so-called planimetric warm-ups. |
| BISWAS Md. Haider Ali " Mathematical Model for the Study of Contagious Vector-borne Zoonotic Disease Nipah Virus Infection " - from the section: Differential Equations, Dynamic Systems and Their Applications A mathematical model to describe the nipah virus (NiV) transmission from bats to human and human to human is propounded here. We propose this model with the focus on the construction of the basic reproduction number and related stability analysis for the disease free and endemic equlibira. The basic reproduction number that represents the epidemic indicator is obtained from the largest eigenvalue of the next generation matrix. It is shown that the disease free equilibrium is stable only when the basic reproduction number is less than one, which means that the disease can be eradicated under such condition in finite time and unstable when greater than one. When the associated reproduction number is greater than one, the endemic equilibrium is stable. Numerical simulations are shown to support the presented analytical results. |
| BOČKOVÁ Veronika " Design of Non-Routine Problems in Training of Future Primary School Teachers with Emphasion on Application " - from the section: New Trends in Mathematical Education The primary school students have a lot of knowledge of mathematics which they need to understand and employ in their future daily live. The standard tasks usually support the below cognitive skills. Unlike them, the non-standard tasks are helpful to gain the informal knowledge and approximate mathematics to the pupils´needs. In the contribution we introduce experiences of future primary school teacher with creation and inclusion of the some non-standard tasks in educational process. |
| BRANNY Michael " The Constructions of Inscribed Regular Polygons with Compass " - from the section: New Trends in Mathematical Education Mohr-Mascheroni constructions are constructions with restricted means. These constructions are proved to be equivalent to euclidean constructions. [6] The paper deals with the issues of selected constructions only with compass. The constructions of selected inscribed regular polygons will be presented. |
| BRUNETTI Federico Alberto " The Modulation of Shape. Radiocentric and Reticular Morphology. Some Design Didactic Experiences in Learning by Doing Through Analogic Nature and Technical Algorithm. " - from the section: Mathematics and Art The understanding of shapes in the real space takes place through a complex and articulated process that makes interact: the visual and tactile perception, the acquired knowledge of a series of elementary geometric shapes and their derivatives, the capacity for mental modeling of space. This educational research presents two case studies that I consider interesting in the development of this formative dynamism, through the integration and exercise of the observation, modeling and projectural reinvention of the forms for design. The methodology adopted here has been inspired taking into consideration the mathematical procedures of spatial organization of complex shapes, through the radiocentric vegetal morphologies and the reticular modulated waves and dome coverage of recent public buildings in Milan. The preliminary realization of analogical structural models was subsequently integrated by the use of modeling software (sketchup, 3Dstudio max, meshmixer (AUTODESK), Kubity, superformula), and potentially therefore towards the realization of models in 3D printing. The aim of these experiments was to integrate the learning of the manual and tactile acquisition of the modeling of the space with the practice of digital modeling as a path to virtualization of form knowledge, considering also the morphological creativity in control complex shapes for design. These specific training courses took place within the framework of the new training methods defined in Italy in the recent Alternanza Scuola Lavoro procedures (in collaboration with Parco Nord Milano and the Accademia Fondazione Fiera Milano), where the training in soft skills is integrated. with the knowledge of specific and ordinary didactic disciplines. |
BUDÍK Ladislav |
| BUDÍKOVÁ Marie " Advanced Course of Applied Statistics for Anthropology Students: The Teaching Process " - from the section: New Trends in Mathematical Education In this paper we will describe the advanced course of statistics for anthropology students at Masaryk University. Teaching statistics to students of non-mathematical fields is typically a challenging issue. Students are more motivated to learn when they can see a direct application of statistics in their own field, therefore we prepared exercises in collaboration with the Department of Anthropology. |
| BUKACEK Marek " Statistical Analysis of Old Kingdom of Egypt " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The first results of analytic approach applied to Egyptology data are presented. The titles distribution among population illustrates the structure of the Old Kingdom of Egypt. The interactions between titles were analysed using conditional probability of occurrence, correlation and contingency tables. Each of methods was tailored with respect to the data to bring easily readable analytic output, as illustrated on case studies. |
| BULKOVÁ Kristína " Zig - zag Functions in Mathematical Open Ended Problems for Functional Thinking Development " - from the section: New Trends in Mathematical Education Mathematics B-day is the team contest with focus to the process skills in mathematics problem solving of upper secondary students. Thus the principles of the contest are necessary to introduce to students in initial teachers’ mathematics education. In one of the recent assignments the zig-zag functions are defined. The potential of the assignment for building pedagogical subject knowledge and nurture the subject content knowledge, functional thinking, is discussed in the article. |
| CANDITO Cristina " Between the Second and Third Dimension:Isometric Configuration in Art " - from the section: Mathematics and Art The present contribution examines the characteristics and reasons for the recurrence in graphic language of plane tessellation that can be assimilated to isometric orthogonal axonometry: a peculiar case where the two-dimensional configuration acquires a three-dimensional meaning. Known since ancient times, its suggestive effects were used in a series of artistic expressions in the twentieth century as well as in the graphic language of today’s music videos. |
| CAPANNA Alessandra " The 8 and the Taranta. An Urban Project “ad quadratum” for Melpignano (LE) " - from the section: Mathematics and Art The research about the Measure and the Project, that has a strong mathematical issue because it takes into a close relationship geometry, number, music and shape, gave origin to a proposal to reshape the area in which the concert of folk music named Taranta takes place in Melpignano every year. Melpignano is a small town in Salento (south of Italy) characterized by a strong heritage which becomes the starting point for the project. The research steps consisted on the study of the cultural context and the description of the important soundscape aspect of the place in which the Taranta concert takes place. The first part of the studies concerned the analysis of the site and of the urban structure from which we have derived the historical measure, using the tool of the survey, but also through the reading of Ernesto De Martino’s ethnomusicological studies about the Salento folk songs. To define the compositional idea, it was important a general knowledge of the myths belonging to the local culture, for example the inhabitants thought that a sort of musical exorcism was able to heal the bite of the Tarantola spider. The 80 “palmi napoletani” measure of the module and the recurrence of the number 8 that we can find also in the physical characteristics of the spider allowed us to construct a geometric grid structuring the project “ad quadratum”. The hypothesis of the project is based on the geometric mathematic method in order to design new spaces starting from the interactions between sound and lights organized according to the historical measure. The aim of this paper is to present the first step of the project concerning the geometric construction of the grid to set the urban layout of the spaces dedicated to the concert of the Taranta. |
| CEPPITELLI Rita " Continuous Utility Functions in Mathematical Economic Models " - from the section: New Trends in Mathematical Education In Economics, preference relations (or preorders) are often described by means of utility functions. We are interested in continuous utility representations of not-total (partial) preorders. Not-total preorders are usually considered in the context of decision-making under uncertainty and risk. In this paper, we present two mathematical models described by not-total preorders. The first model is the Lorenz ordering (a preorder defined by the Lorenz curves) on the set of all distributions of wellbeing of a given population. The Lorenz curve is an effective way to show the inequality of the income within and between populations. An example of utility function representing the Lorenz ordering can be given by the Gini coefficients. The second mathematical model is the Finite dimensional State Preference Model where a not-total preorder is defined by linear operators on financial markets. Both models can be extended in submetrizable k_omega-spaces (when the size of the population varies or when the number of goods in the portfolios varies) and the preorders can be described by the application of generalized representation theorems for submetrizable k_omega-spaces. |
| CHEREVKO Yevhen " Almost Geodesic Mappings of the Second Type of Spaces With Affine Connection onto Two-Symmetric Spaces " - from the section: Algebra and Geometry and Their Applications In the paper we consider canonical almost geodesic mappings of the second type of spaces with affine connection onto two-symmetric spaces. The main equations for the mappings are obtained as a closed mixed system of PDEs of Cauchy type. We have found the maximum number of essential parameters which the solution of the system depends on. |
| CHVALINA Jan " Models of Iterated Artificial Neurons " - from the section: Algebra and Geometry and Their Applications Application of algebraic structures in research of structure of the most used artificial neural network - multilayer perceptron and functionality of artificial neuron, is one from current the most interesting areas in the usage of time varying artificial neurons. In this paper, we have described certain properties of constructed algebraic structures of artificial neurons, including the hypergroup formed by iterated models of artificial neurons. We describe constructions of P-hypergroups - a certain special case of which are variants of semigroups - of artificial time-varying neurons based on investigations of Vougiouklis - Konguetsof and also construction of the cascade with the phase set of neurons. These concepts yield a base for the building of algebraic systems of artificial neurons which deserves to be developed. |
| ČIERNIKOVÁ Dominika " Possibility of Choosing the Open or the Closed Task and Looking at the Reasoning of the Chosen Option " - from the section: New Trends in Mathematical Education Some new trends in mathematics teaching involve using open tasks in math classes. Taking to consideration the principles of the Highly Effective Teaching Model we gave a group of 17 nine-graders (14 – 15 year old) a set of tasks and they could choose to solve an open or a closed task providing the reasons why they chose the one. The same set of tasks was given to future mathematics teachers and they were supposed to give opinions which options would be more attractive for pupils and why. |
| CONSTANT Jean " Knowledge Visualization, Stochastic Processes and Visual Art " - from the section: Mathematics and Art With the predominance of screen-based technology, the volume of visual material we need to process grows exponentially. Unfortunately, the process by which we access, interpret and share insight has not progressed as quickly asserted G Judelman in his thesis dissertation. The constraints of the cognitive and perceptual systems, or the social context it originates from, requires a system which cannot only present information but communicates knowledge. The Knowledge Visualization framework is a fairly recent concept that examines the use of visual representation to improve the production and transfer of knowledge. The process of Knowledge Visualization incorporates information data in its framework along with additional steps such as gathering, comprehending, interpreting, organizing, designing, and communicating the information. This talk will present a brief overview of the framework methodology, and based on a current research project I am involved in, demonstrate in practical terms how, tapping various sources of information in mathematics, probability theory, and computer sciences, I successfully reconstructed a series of visual statements and shared them with scientific and general audiences, obtaining in the process some unexpected but meaningful new knowledge. |
| DLOUHÁ Dagmar " Knowledge Asessment of Student´s High School Mathematics " - from the section: New Trends in Mathematical Education Unacquaintance of high school mathematics is a problem that accompanies students at VSB-TU Ostrava during the whole period of study. In this article, we will introduce you to the results of a questionnaire survey among students of the first year, in which they should evaluate their knowledge of high school mathematics themselves. We compared their subjective opinion with the results of our testing carried out in preparation of new admission procedures at VSB-TU Ostrava. |
| DOTLAČILOVÁ Petra " Methods Used for the Calculations of Normal Length of Life " - from the section: Financial and Actuary Mathematics Today it is important to have very good analysis of mortality. For this, it is possible to use, for example, the normal length of life (or age modality of deaths). The aim is to present different ways of estimating the mentioned indicator. At the same time, an estimation formula can be derived that can be used to calculate normal length of life. In this article, the normal length of life will be estimated using the Weibull model. The second method will be the approximate estimate of the age to be analysed. |
| DVOŘÁKOVÁ Stanislava " Evaluation of the Equalizing Course of Mathematics at VŠPJ During 2012-2018 " - from the section: New Trends in Mathematical Education Department of Mathematics at College of Polytechnics Jihlava (VŠPJ) organizes equalizing courses of mathematics for its future students in order to make easier studies of mathematical subjects. The course takes place once a year. The content of the course is the revision of the basic knowledge of mathematics from a secondary school. All students, who had passed the course in the last few years, filled in an anonymous questionnaire in order to evaluate the course. In this paper we evaluate these questionnaires. In addition, we present the numbers of students from this course depending on the study programme and form of study during 2012-2018. |
| DZENITE Ilona " New Practical Methods of Analysis of Second Order Curves on a Plane " - from the section: New Trends in Mathematical Education In this work second order curves have been studied in all their diversity as they appear in applications. These curves have been examined without using the concept of rotation, a concept which is introduced artificially in textbooks in order to simplify the basic form of the canonical equations of these curves: a concept which is only used for inclined second order curves, and which is both intimidating and difficult for newly accepted university students. A new methodological approach based only on completing the perfect square has been proposed, and generalized formulas of equations for an ellipse, a hyperbola and a parabola have been obtained. The use of these formulas has been shown in particular examples of the study of several inclined second order curves, analyzing their basic characteristics and graphing. The new generalized formulas of ellipse and hyperbola equations seem absent in literature. |
| FAJKUSOVÁ Michaela " Limit−Point/Limit−Circle Problem: Continuous vs. Discrete Case " - from the section: Differential Equations, Dynamic Systems and Their Applications The limit−point/limit−circle classification for second order linear difference equation is introduced. Limit−point as well as limit−circle criteria are established based on the equivalency among second order difference equation, recurrence formula and symplectic system. Finally, we compare a special type of differential and difference equation with respect to limit−point/limit−circle property and we show some discrepancies between continuous and discrete case. |
| FERDIANOVA Vera " The Constructions of Inscribed Regular Polygonswith Compass " - from the section: New Trends in Mathematical Education Mohr-Mascheroni constructions are constructions with restricted means. These constructions are proved to be equivalent to euclidean constructions. [6] The paper deals with the issues of selected constructions only with compass. The constructions of selected inscribed regular polygons will be presented. |
| FERREIRA Manuel Alberto M. " Laplace Transform Effectiveness in the M|G|∞ Queue Busy Period Probabilistic Study " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The Laplace transform is a widely used tool in the study of probability distributions, often allowing for a probability density functions and distribution functions simpler determination and being a “moments generating function”. In this paper it is considered a situation not so simple, as it is the case of the M|G|∞ queue busy period length distribution. Attention will also be given the respective tail Laplace transform. Then, in the context of an open queues network, which nodes behave as M|G|∞ queues, the Laplace transform will be used to construct an algorithm to determine the Laplace transform of the global service time length of a customer during their stay on the network distribution. Key words. Laplace transform, M|G|∞, busy period, queues network, algorithm. Mathematics Subject Classification: 44A10 and 60G99 |
| FESZTEROVA Melania " Evaluation of the Ration of Total Organic Carbon to Total Nitrogen in Soil (Kremnické and Štiavnické Mountains) " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise Nitrogen naturally recovers in the soil within its cycle. The lack of major nutrients, including nitrogen, is rapidly reflected in the level of plant production. Its additional input is needed to obtain higher yields when the natural nitrogen supply is not enough to achieve the target yields. Nitrogen has a significant environmental status. In the upper layers of agricultural soils there is an average of 0.14-0.26% NT, which is a fertility factor as is humus content. The impact of soil spatial diversity, soil conditions and time variability on the total carbon content of soil, to the total nitrogen content represents not only their determined values, but also the statistical processing and evaluation of measured data. The aim of the paper is to describe the use of parametric tests in the assessment of selected soil characteristics. To assess the impact of environmental and ecological relationships with regard to selected soil characteristics, different statistical methods have been used. The results obtained were evaluated and graphically processed using the statistical software STATISTICA at the level of significance of α = 0.05. Several statistical methods have been used to evaluate the selected soil characteristics (TOC, NT). The application of statistical methods is important in the field of environmental monitoring, where the processing of data and the search for interrelationships is important. |
| FILIPČUKOVÁ Alena " Flow Charts Application in Education " - from the section: New Trends in Mathematical Education This paper deals with possibilities of flow charts application in education. Flow charts can be applied in various subjects on all grades of schools and universities. They can variegate and contribute to a better education and make the curriculum more synoptical. The paper presents flow charts regarding linear algebra, differential calculus of functions of one variable and partial differential equations. It is pointed out how to use flow charts and how to use them most effectively in education. |
| FILIPE José António " A Queue Model to Monitor the Conversion from ICEV to EV, HEV and DV in a Scarce Oil Environment " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise Grounded on the M|G|∞ queue system, we build a model to analyze a situation in which ICEV-Internal Combustion Engine Vehicles, moved only by the action of an internal combustion engine, get idle, in a scarce conventional energy ambience, and are either recycled, turning either EV-Electric Vehicles or HEV-Hybrid Electric Vehicles, or dismantled becoming DV-Dismantled Vehicles. We model the three situations: EV, HEV and DV with the same purpose. The model allows concluding that when the rhythm ICEV become EV, HEV and DV is greater than the rate at which they become idle the system has a tendency to balance. In addition, we perform a cost-benefit analysis. Keywords. ICEV, EV, HEV, DV, M|G|∞, hazard rate function. Mathematics Subject Classification: Primary 60G99; Secondary 91F99. |
| FIŤKA Ivan " Data Warehousing for On-Line Identification " - from the section: Mathematics and Physics in Contemporary Science and Technique This paper deals with creation of an optimal database structure suitable for algorithms requirement of on-line identification which was used together with spline based predictive controller (SBPC) by long-term experiment on heat exchanger station (HES). The aim is to show some simply theorem and methods for design of more reliable adaptive control schemes based on on-line system identification. In the contribution various kinds of problems are solved, which was caused by experiment features (for example: HES nonstop operation, progress of stochastic errors of measured data, switching between different working points of HES (day, night, weekend...) or our software and hardware solution). At the end of the contribution quality comparing between our solution and industrial PID controller is enclosed. |
| FRAILE REY Arantzazu " Counteracting Detachment and Enhancingunderstanding through E-Learning in Mathematicswith Engineering Students " - from the section: New Trends in Mathematical Education We present a case study regarding the mathematical education of prospective engineers. To cope with the growing lack of attendance, e-learning tools were used in the framework of a flow process regarding the days before the lesson, the lesson itself and the assessment of learning. Initial notes create in students the desire to attend the lesson, thanks to the link between math concepts and the real world, and professional practice. The approach is presently applied with success. |
| FULIER Jozef " Some Aspects of Teaching Calculus in Mathematics Teacher Education: The Case of Infinite Series " - from the section: New Trends in Mathematical Education In our contribution we present one basic example of the use of history of mathematics helping lecturers as well as learners understand and overcome epistemological obstacles in the development of mathematical understanding of infinite series. Based on the principle that “ontogeny recapitulates phylogeny” – we justify as appropriate that the development of an individual’s mathematical understanding respect the historical development of mathematical ideas, in this case of infinite series. |
| GABKOVÁ Jana " Active Learning Methods in Engineering Mathematics - Adventure and Challenge " - from the section: New Trends in Mathematical Education Paper brings information on experience with introduction of innovative active learning and teaching methods into basic course Mathematics I for the first year engineering students at the faculty of Mechanical Engineering, Slovak University of Technology in Bratislava, Slovakia. Evaluation of experiment results and students achievements is presented in statistical data. Supplementary analysis of feedback obtained from students in questionnaire shows insight into students opinions on various teaching scenarios and comparison of used methods of eduScrum and individual study. |
| GAŠPARÍK Marek " Test Design of the PID Controller for Controlling the Electro-Hydraulic Piston " - from the section: Mathematics and Physics in Contemporary Science and Technique Following this publication, the article deals with a different measurement method for the aforementioned control system, which provides automatic control of the clutch pedal in a car for disabled people. This part of the system will be used to measure the force acting directly on the transmission lever when the gear is engaged by a human hand and its action by an electric-piston plunger. The article mainly deals with the processing of the measured values and the design of the PID / PSD regulator for the control of the electro-hydraulic piston, which controls the clutch system in the automobile. |
| GAVALA Tadeáš " Preparing Future Mathematics Teachers to Apply Inquiry Approaches to Teaching " - from the section: New Trends in Mathematical Education The official documents for the EU´s education policy emphasize the importance of development of competencies related to innovative teaching and assessment strategies in initial teacher education. Key recommendations for mathematics teaching are focused on learner-centered approach based on inquiry-based learning. Important conditions for successful integration of inquiry approaches to teaching are supplementation of the educational content with examples of inquiry activities and development of teachers´ competencies for application of inquiry approaches to mathematics teaching. The paper describes an inquiry activity to explore and analyse the results of a coin game that could be implemented to the probability teaching in secondary schools. The aim of the proposed inquiry activity is to provide the opportunity for future mathematics teachers to test inquiry work and to use experience for evaluation of the suitability of prepared teaching materials to stimulate students´ engagement in inquiry learning. Future teachers are also required to complete some parts of the teaching materials and to provide suggestions for successful realization of the inquiry activity in mathematics teaching. These partial activities focused on planning and preparing the inquiry activity and its evaluation are intended to inspire future teachers to use different forms of the formative assessment, which should be an important part of the inquiry-based learning. In the conclusion of the paper, we describe the results and the summarized experience received from the realization of the inquiry activity on courses of didactics in daily and external forms of study for future mathematics teachers in the last year of their study. |
| GERGELITSOVÁ Šárka " The Importance of Reading Instructions " - from the section: New Trends in Mathematical Education We use data about thousands of students’ answers to tasks in online system GeoTest and we look at mistakes they made and how they succeed to find the source of the mistake. It shows that source of some errors is simply poor reading or misunderstanding the instructions and also that many students are nor able to find and correct their mistake. We guess that these problems relate to general attitude of the student to problem solving. |
| GLIVICKÁ Jana " Quantum Computing in Computer Science Curricula in the Czech Republic " - from the section: New Trends in Mathematical Education Quantum computing and quantum technology in general is a growing and promising field of research and industry. The aim of this paper is to review the offer of courses in quantum computing to computer science students at selected universities in the Czech Republic. We also suggest resources and basic outline of a course in computer science available to undergraduate students with no particular background in quantum physics and linear algebra. |
| GLIVICKÝ Petr " Metaphors in Teaching Infinity: Limits, Cardinalities, and Nonstandard Models " - from the section: New Trends in Mathematical Education Mathematical conception of infinite quantities forms a cornerstone of many disciplines of modern mathematics --- from differential calculus to set theory. In fact, it could be argued that the most significant revolutions in mathematics in the modern period were always triggered by a development in our understanding of infinity. From the pedagogical point of view, the students´ comprehension of the concept of infinity is a competence of interdisciplinary value, helping them to grasp the reasons why and how individual disciplines of modern mathematics were built up. In this paper we present a number of illustrations, examples, and allegories that illuminate and clarify different aspects of infinity. The author has been using and gradually developing these metaphors for infinity in his undergraduate and graduate courses and popular lectures on mathematical logic, set theory, calculus, and nonstandard analysis during the last decade. The aim of this paper is to share the accumulated didactic know-how. |
| GRAF Vojtěch " Operational Planning of Flight Crews with Minimisation of Transfers of Pilots to Airports " - from the section: Modeling and Simulation in Engineering and Scientific Computations The article is focused on presenting possibilities of linear programming methods for operational planning of flight crews. The mathematical model presented in the article takes into account different operational and legislative restrictions resulting from conditions for flight crew management. The mathematical model matches pilots to create the flight crews and assign them to planned flights. An optimisation criterion which is used in the model represents costs of transfers of the pilots to airports where the pilots report for duty. |
| GREBLIČKI Marijana " A Different Approach to the Volume of Pyramids and Cones " - from the section: New Trends in Mathematical Education In this paper we discuss the volume of a quadrilateral regular pyramid, a general quadrilateral pyramid and a general cone, from a new aspect. Of course, the volume of a general quadrilateral pyramid and a general cone can be calculated using an integral account, but there are certainly other ways to avoid using such a powerful tool as a double or triple integral. One such interesting approach to the above-mentioned problem is presented in this contribution. |
| GROSINGER Patrik " Analog Computer from Modern Components " - from the section: Mathematics and Art An analog computer is an electronic device that has been designed primarily to solve differential equations and their systems. This article describes the construction of this currently unused device using modern integrated circuits. It also describes its use for solving some differential equations and their systems. |
| GUDYREVA Olena " On the Conformal Mappings of Special Quasi-Einstein Spaces " - from the section: Algebra and Geometry and Their Applications We have studied the conformal mappings of special quasi-Einstein spaces. We have proved that they are closed with respect to concircular mappings. We have introduced the notion of mobility of pseudo-Riemannian spaces with respect to concircular mappings. The tensor characteristic of maximal mobility for special quasi-Einstein spaces has also been found. |
| HAŠKOVÁ Simona " The Alternative to the Bayesian Procedure: Visualization of the Problem by Means of the Tools of Logic " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise Traditional calculation procedures based on conditional probability rely on the Bayesian formula. The findings of psychologists argue that this approach is often unacceptable, leading to many errors. The paper examines ways contributing to error reduction occurrences in probabilistic calculations. They include the frequency approach based on the models of the Venn diagram and the decision tree. Bayesian model is described in a novel way as a complex of statistical and casual ratios. |
| HLAVOVÁ Marta " Approximation of Helix in CAD/CAM Systems " - from the section: Algebra and Geometry and Their Applications This contribution is focused on approximation of a cylindrical helix used in some available CAD/CAM systems. The comparison of curves approximating a particular helix segment is given and two new types of approximation with a rational Bézier cubic curve are introduced. The approximation accuracy of all considered curves is compared with respect to the curvature, slope and deviations of each curve from a set of theoretical points and the base cylinder. |
| HOLAN Tomáš " The Importance of Reading Instructions " - from the section: New Trends in Mathematical Education We use data about thousands of students’ answers to tasks in online system GeoTest and we look at mistakes they made and how they succeed to find the source of the mistake. It shows that source of some errors is simply poor reading or misunderstanding the instructions and also that many students are nor able to find and correct their mistake. We guess that these problems relate to general attitude of the student to problem solving. |
| HONZIK Lukas " Examination of Properties and Important Elements of Binary Operations in Future Mathematics Teachers’ Education " - from the section: Algebra and Geometry and Their Applications In order to prepare our students – future teachers of mathematics for potential problems, their pupils may encounter in math classes when working with binary operations, such as addition, multiplication, etc., subjects Elementary Algebra and Mathematics and Its Teaching Methodology are included in the study plans. In these subjects, when working with unusual binary operations, students get into the role of the pupils and are forced to think about each next step in their investigation. |
| HORSKÝ Richard " Some Methods How to Solve the Ill Posed Problems " - from the section: Algebra and Geometry and Their Applications The term ill-posed problem is popular in modern science since the middle of the 20th century. It has turned out that a plenty of problems in different areas of classical mathematics (differential and integral equations, functional analysis, computational algebra) can be classified as ill-posed and thanks to their instability and non-linearity they belong to the most complicated. Here are given.some examples and two most remarkable methods for solving of ill-posed problems. |
| HOSKOVA-MAYEROVA Sarka " Automatic Model Building for Binary Logistic Regression by Using SPSS 20 " - from the section: Modeling and Simulation in Engineering and Scientific Computations This article describes the main effects of automatic logistic regression model building by the computer software. To illustrate different techniques which are available for the automatic model building of binary logistic regression the small firms´ internationalisation grow data analysis was chosen and SPSS 20 software, which encloses a wide array of services like data management foresee accurate case-police statistics and different tests alongside their predictions. The model building investigations refer to continuous internationalisation process that consequently leads to the commitment of the firms to international markets. In this reason the best-subset search procedures such as forward stepwise, backward stepwise, forward entries, backward removal, were used to help to identify some of the most significant factors, influencing the development processes of internationalisation of high growth firms (HGFs). Stepwise logistic regression methods, specifically the forwar d stepwise and backward stepwise methods, were used to perform a stepwise selection of predictor variables. All effects of these automatically built models were evaluated by Hosmer-Lemeshow goodness-of-fit test, deviance, Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC) and other tests. Furthermore, the ROC curve analysis was used to measure the goodness-of-fit and to compare the built competing logistic regression models. |
| HREHOVA Stella " Basic Data Analysis Using the Add-In Power Pivot " - from the section: Modeling and Simulation in Engineering and Scientific Computations The ability to effectively manage information and extract knowledge is now seen as a key advantage. It is therefore necessary to look for the tools for their efficient and simple processing that can be handled by common user. The paper describes the use of the MS Excel add-in Power Pivot to analyze selected parameters of the heating process from the measured data obtained from different sources. |
| HRUBÝ Petr " Mathematical Model of Gear Pump Reaction Forces " - from the section: Modeling and Simulation in Engineering and Scientific Computations This contribution is devoted to the University-Industry cooperation. Comparison of empirical and analytical solution of gear pump reaction forces was described. The mathematical model was developed and it was compared with real measured values. It was proposed to improve the model based on results. |
| HUYLEBROUCK Dirk " An Euler-Cayley Formula for General Kepler-Poinsot Polyhedra " - from the section: Algebra and Geometry and Their Applications The formula of Euler-Descartes for a polyhedron with V vertices, F faces and E edges states that V + F – E = 2. On the one hand, it was generalized to polyhedra constituting the atoms repeated in a polyhedral structure with h loops: V + F – E = 2(1 – h). On the other hand, Cayley generalized it to the Kepler-Poinsot polyhedra with V vertices of densities b and F faces of density a, E edges and polyhedron density c: bV + aF – E = 2c. It was generalized to Archimedean polyhedra with Vj vertices and Fi faces of a given type and densities bj and ai respectively, E edges and polyhedron density c: bjVj +aiFi – E = 2c. Here it is shown that the both generalizations can be united in a single formula: bjVj +aiFi – E = 2(c – a1h) where, Vj are the vertices and Fi the faces of a given type and densities bj and ai respectively, E the edges and c the polyhedral density of the atom repeated in the structure with h loops connected on faces with face density a1. We illustrate the formula with several examples of generalized Kepler-Poinsot polyhedra. |
| IANNACE Gino " The Acoustics of the Church of the Holy Family in Salerno (Italy) " - from the section: Mathematics and Art The church of the Holy Family in Salerno is the first sacred building made of reinforced concrete. The work began in 1971 and required a complex work, also with the employment of shipyard workers, for the particular stepped geometry of the roof. In this paper the results of acoustic measurements and spatial distribution of parameters are reported. The measured average acoustic parameter values provide an indication that there are no suitable features for listening to speech and music within the building. |
| IŽOLD Roman " Influence of Gyroscopic Effects on Natural Frequencies of Rotating Shaft " - from the section: Modeling and Simulation in Engineering and Scientific Computations The aim of this paper is to examine an influence of a gyroscopic effect on natural frequencies of rotating shaft and its related seismic response. This paper presents proposal of a numerical analysis and its application on the specific model. The results of numerical analysis clarify conditions for backward modes excitation and demonstrate the difference in the seismic response of rotating and non-rotating shaft. |
| JANČAŘÍK Antonín " Ict in Mathematics Teacher Education " - from the section: New Trends in Mathematical Education A paper focusing on the use of ICT in pre-service mathematics teacher education was presented at this conference ten years ago by me and my colleagues. The aim of this paper is to assess the changes that the use of ICT has undergone in pre-service mathematics teacher education over the past ten years since the time the last paper was published, both in the area of technological equipment available and in the area of curricula of subjects that focus on the use of ICT. |
| JANOŠOVÁ Markéta " Advanced Course of Applied Statistics for Anthropology Students: The Teaching Process " - from the section: New Trends in Mathematical Education In this paper we will describe the advanced course of statistics for anthropology students at Masaryk University. Teaching statistics to students of non-mathematical fields is typically a challenging issue. Students are more motivated to learn when they can see a direct application of statistics in their own field, therefore we prepared exercises in collaboration with the Department of Anthropology. |
| JERÁBEK Róbert " A Numerical Study on a Cantilever Using a Thermodynamically Consistent Hypoelastic-Plastic Material Model " - from the section: Modeling and Simulation in Engineering and Scientific Computations Contemporary hypoelastic-plastic material models for finite-strain elastoplasticity cannot be considered to be thermodynamically consistent. Therefore their results are affected by the description and the particularities of their mathematical formulation. Recently a nonlinear continuum theory for finite deformations of elastoplastic media have been proposed, which allows for the development of thermodynamically consistent material models. In this paper a numerical study on a cantilever beam is presented using a thermodynamically consistent material model. |
| JOVIC Biljana " Golden Section: Applications in Domain of Landscape Architecture " - from the section: Mathematics and Art This paper deals with the analysis of the relationship between natural structures and golden cross sections, as well as the application of the golden cross section in the domain of landscape architecture. The aspects and research results shown in this paper are concerning the geometric construction of the golden section and its applications by the elements of visual aesthetics in landscape architecture as the basic elements of the composition. The aim of the paper is the systematization of elements from the aspect of using the golden section, as well as the application on concrete examples in domain of landscape architecture. |
| JURSA Andrej " Clique Number Estimate in Uncorrelated Scale-Free Networks " - from the section: Modeling and Simulation in Engineering and Scientific Computations In this paper, we analytically estimate clique number for scale free networks. The estimate is done by two different yet related methods. In order to test the quality of our estimate we made a specialized network generator. With a help of this generator, we are able to create a network with the prescribed degree distribution. The resulting networks are connected and uncorrelated. The clique number is then exactly calculated with a help of our original algorithm and compared to the estimated values. |
| KAMIENIEVA Alla " Mappings of Spaces with Affine Connection Preserving the Weyl Tensor " - from the section: Algebra and Geometry and Their Applications While modeling physical and other objects with a help of mappings, it is important to know whether the properties of "original" are preserved in "image". The space of affine connectivity is characterized by a certain set of tensor objects. There is Weyl tensor among them. The paper presents conditions, that are necessary for preservation of Weyl tensor in the course of the mapping of the space of affine connectivity on another space of affine connectivity. |
| KARSAI János " On the Impact of Vaccination on the Epidemiology of Varicella in Hungary " - from the section: Differential Equations, Dynamic Systems and Their Applications Varicella is one of the most common infectious diseases of children, which can be prevented by vaccine. Varicella causes not only the chickenpox of children, but also the herpes zoster at an older age. In Hungary, the vaccine is available for many years, it is planned obligatory. There has been hardly any study neither on its impact nor the effectiveness of vaccination strategies. The epidemiology of the varicella-zoster virus (VZV) is quite complicated. Upon recovery from the varicella infection, VZV remains in the body in latent form. In general, the individual has lifelong immunity to VZV, but the immunity can be waning, the virus may reactivate and causes zoster. Zoster infected people are also infectious. Hence the modeling must take into account both the short period of infections (weeks) and long-time consequences (years), as well as the age-structure of the population. In addition, based on a widely accepted hypothesis of exogenous boosting, contacting with an infected person will boost the waning immunity. Now, vaccination against VZV decreases varicella infections and this boosting effect, then the infections of herpes-zoster will increase in 20-30 years due to the lack of immunity boosting. In our talk, we consider different models of varicella infections including vaccination strategies taking into account the Hungarian specialties. We study the available demographic and epidemiological data, perform parameter estimations and present Wolfram Mathematica experiments for the possible consequences of the different vaccination strategies. Acknowledgments: This research is supported by the EU-funded Hungarian grants EFOP-3.6.2-16-2017-00015 and NKFIH KH 125628. |
| KIOSAK Volodymyr " Mappings of Spaces with Affine Connection Preserving the Weyl Tensor " - from the section: Algebra and Geometry and Their Applications While modeling physical and other objects with a help of mappings, it is important to know whether the properties of "original" are preserved in "image". The space of affine connectivity is characterized by a certain set of tensor objects. There is Weyl tensor among them. The paper presents conditions, that are necessary for preservation of Weyl tensor in the course of the mapping of the space of affine connectivity on another space of affine connectivity. |
| KLEŠČ Marián " The Crossing Numbers of Join of Cycles with Graphs of Order Four " - from the section: Algebra and Geometry and Their Applications The crossing number cr(G) of a graph G is the minimal number of crossings over all drawings of G in the plane. According to their special structure, the class of Cartesian products of two graphs is one of few graph classes for which some exact values of crossing numbers were obtained. Lately, there is a great interest in studying the crossing numbers of join products of special graphs. The obtained results can be used in establishing the crossing numbers of Cartesian products of trees with special graphs. There are known the crossing numbers of join products of graphs of order at most four with discrete graphs and with paths. In the paper, we extend these results by giving the crossing numbers of join products for all graphs of order four with cycles. |
| KLUFA Jindrich " Relation Between University Study Results in Math and Admission Procedure " - from the section: New Trends in Mathematical Education The study results in mathematics at University of Economics in Prague are analysed in present paper. The analysed data are the results in mathematics of 240 students in winter semester of the 2017/2018 academic year in the course Mathematics for informatics. Dependence these results on admission procedure at the Faculty of Informatics and Statistics at University of Economics is studied in the following text. Different statistical methods were used for the study this dependence (descriptive statistics, one-way analysis of variance, Bartlett’s test, Kruskal-Wallis nonparametric test). |
| KMEŤOVÁ Mária " Problem Solving in Dynamic Geometry Environment Using the Intercept Theorem " - from the section: New Trends in Mathematical Education The contribution is devoted to a qualitative research on geometry problem solving by university students. To observe how prospective mathematics teachers are able to utilise advantages of dynamic geometry environment (DGE) in geometry problem solving, case studies were conducted. The process of problem solving, in which the intercept theorem was needed to be used, was followed individually with all participants of the experiment and recorded in details. The paper collects the results on creating the proof in DGE. |
| KONEČNÁ Petra " The Problem of Evaluation in Ects System and Its Mathematical Solution " - from the section: New Trends in Mathematical Education In connection with introduction of an alphabetical classification scale based on ECTS evaluation, courses are also evaluated by the point score that corresponds to a percentage result and also serves for transfer between individual classification systems. This point score often does not match previously used point scores for evaluation of student´seffort. The contribution introduces solution to this problem; there is found a function that converts points obtained from each separately evaluated part of the whole test to an integer on scale 0-100 so that if a student does not reach the minimum required score from each sub-section, his/her overall rating will be in interval ⟨0,51), and he/she it reaches, it will be within range ⟨51, 100⟩. Assigned points at both intervals corresponds to the overall performance of the student. |
| KONTRIKOVA Lenka " Optimization Flight Routes " - from the section: Modeling and Simulation in Engineering and Scientific Computations During the planning a flight between two aerodromes, the crew must has to take so many number of factors, which can affect the difficulty execution flight and which can influence the course of flight. When the real process is formulated as a set of limiting factors, and the most appropriate solution has to be chosen from multiple solutions, such a task may be considered an optimization problem. To optimize the problem of choosing the most suitable flight route, operational research can be further solved, which offers the appropriate methods for this. The article describes a possible mathematical approach to solving the given issue in terms of IFR flights. It deals not only with the issue of taking into account the limiting factors, but also with the choice of an appropriate optimization criterion that will allow the effectiveness of the proposed solution to be evaluated. Because this application is very specific, other contexts that affect flight planning must be described. In particular, it is a guideline for the proper construction of a chart, in which the flight route is then optimized. |
| KORENOVA Lilla " Calculator as a Supporting Tool in Mathematics Education at University Level " - from the section: New Trends in Mathematical Education Universities’ freshmen are often facing problems in their courses requesting deeper mathematical knowledge and skills. The problems are rooted in their insufficient prerequisites and absence of routines in complex calculations after graduating high schools. A proper incorporation of calculators could diminish a substantial part of the problems and allow them to concentrate on the explained subject and its applications. In our paper we demonstrate examples of this approach. |
| KOŠŤÁLEK Josef " Solving Traveling Salesman Problem by Heuristic Algorithms " - from the section: Modeling and Simulation in Engineering and Scientific Computations This paper describes real model solving the traveling salesman problem using heuristic algorithms. Heuristic algorithms select improbable solutions and therefore the optimal solution is found in a short time. The algorithm uses random search and also regularity in traveling salesman problem’s. At the same time, it is ensured that the algorithm always finds the acceptable solution. |
| KOŤÁTKOVÁ STRÁNSKÁ Pavla " Solving a Deployment Problem with Restricted Areas " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise Our paper describes solving the Weber-Steiner’s problem with restricted areas, where the central point can not be placed. We consider the situation of a set defined points to which we want to insert a central point. We are looking for the optimal position of this central point to transportation costs between central point and the set points will be minimal. We are thinking also modifying this problem with restricted areas, where the central point. |
| KOVÁCS Zoltán " Teaching Inversion Interactively with Webcams Via CindyJS " - from the section: New Trends in Mathematical Education A new visualization method is presented to demonstrate basic properties of circle inversion. The method is based on using a web browser, the web camera of a computer that is enabled in the web browser, and some JavaScript code provided by the CindyJS library. The new approach in slightly modified forms can be used both as a teacher presentation and a student activity that deepens knowledge. |
| KOVÁCS Edith " On the Parameter Design of a Statistical Model Via Bayesian Optimization " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The proper design of parameters of mathematical model is a frequent problem in different fields of science and engineering. If the model can be expressed explicitly as a function depending on a set of parameters and in addition the cost function has “good properties”, there are plenty global optimization methods for finding the optimal set of parameters. In the talk we suppose the model is an unknown function called “black box” which has to be parametrized to be close to certain sample points. The cost function quantifying the goodness of the model can be evaluated for different parameter sets. Since the cost function cannot be minimized directly since it is expensive to evaluate, or because of the lack of good properties such as convexity, derivability, we will use Bayesian optimization (BO). The BO method has been used to design engineering systems, lately it gains much interest in tuning hyper-parameters for deep neural networks, as well as to design hyper-parameters for other machine learning methods. The idea is to define an acquisition function, which is much easier to optimize. We transform the problem into a sequential optimization problem. We gain new information at each step which reduces the uncertainty of the model. The method can be used typically for vector parameters with dimension less than 20 and the number of evaluations performed limited to some hundreds. We illustrate the usefullness of the method on a practical problem. Acknowledgements: This research is supported by the EU-funded Hungarian grants EFOP-3.6.2-16-2017-00015 and The research reported in this paper was supported by the Higher Education Excellence Program of the Ministry of Human Capacities in the frame of Artificial Intelligence research area of Budapest University of Technology and Economics (BME FIKP-MI/SC). |
| KRČEK Jiří " 1. Interactive Tools for Teaching of Numerical Methods for Root-Finding; 2. New Conception of Admission Examination in Mathematics at VŠB-Technical University of Ostrava " - from the section: New Trends in Mathematical Education 1. The aim of the paper is to present our approach for education of numerical mathematics based on the usage of interactive educational tools and materials. In the paper, some tools for teaching numerical root-finding are described. For better understanding of methods principle and for visualizations, we prepared the set of GeoGebra applets which are accessible on the websites for usage. 2. The admission examination in mathematics at the technical faculties of the VŠB – Technical University of Ostrava for the present consists of 6 open problems. Since the academic year 2018/2019 this examination will be replaced by tests with 20 questions in order to examine the wider range of knowledges as well as to implicate problems of various difficulties. The proposal admission examination we have tested on students of the first form at four faculties of the VŠB – TUO. |
| KRIVÁ Zuzana " Speckle Removing Anisotropic Diffusionbased on PDE Models Discretized by the Finite Volume Method " - from the section: Modeling and Simulation in Engineering and Scientific Computations In this paper we deal with speckle removing anisotropic diffusion SRAD with focus on radar imaging applications. Radar images are corrupted by heavy noise called speckle which degrades their quality and makes their interpretation difficult. The filters are required to average homogenous areas and to preserve details. SRAD refers to anisotropic diffusion adjusted for multiplicative noise. In this paper we discuss the finite volume discretization for this model and we derive a stable explicit scheme. |
| LAŠŠÁKOVÁ Vladimíra " Escape Game as an Innovative Tool in Education of Future Mathematics Teachers " - from the section: New Trends in Mathematical Education The paper focuses on the possibility of using escape games in education, namely in education of future mathematics teachers. The paper contains an overview of pedagogical phenomena that are observable in an escape game as well as concrete examples of puzzles from escape games that focus on mathematical concepts. Acquired knowledge is being applied in an escape game that is being built at the Comenius University in Bratislava. |
| LESECHKO Olexandr " Mappings of Spaces with Affine Connection Preserving the Weyl Tensor " - from the section: Algebra and Geometry and Their Applications While modeling physical and other objects with a help of mappings, it is important to know whether the properties of "original" are preserved in "image". The space of affine connectivity is characterized by a certain set of tensor objects. There is Weyl tensor among them. The paper presents conditions, that are necessary for preservation of Weyl tensor in the course of the mapping of the space of affine connectivity on another space of affine connectivity. |
| LESHCHENKO Svitlana " Almost Geodesic Mappings of the Second Type of Spaces With Affine Connection onto Two-Symmetric Spaces " - from the section: Algebra and Geometry and Their Applications In the paper we consider canonical almost geodesic mappings of the second type of spaces with affine connection onto two-symmetric spaces. The main equations for the mappings are obtained as a closed mixed system of PDEs of Cauchy type. We have found the maximum number of essential parameters which the solution of the system depends on. |
| LIU luyi " Cross-Scale in Ancient Chinese Landscape An Exploration of Topological Thinking in Gardens Spatial Design " - from the section: This paper is based on the analysis of two cases of cross-scale spatial design phenomena selected from ancient China. With referring to the ancient Chinese landscape, it tries to explore the application of topological thinking in spatial design. Under this key view, the investigation will help not only to interpret the Chinese gardens but also to show the possibilities of mathematical applications across applied arts and humanities, including their extensions to contemporary landscape architectural design. Keywords: Cross-Scale, Ancient China, Landscape Design, Topological Thinking |
| LIZASOAIN Inmaculada " Learning from Children to Improve Primary School Teachers´ Math-Specific Education " - from the section: New Trends in Mathematical Education The paper describes the design and objectives of ANFoMAM project, supported by the Erasmus Plus Programme in the area of strategic partnerships for innovation in higher education in Europe. To improve primary school teachers´ math specific education, the project takes advantage of a close consideration of children´s way of learning and relationship with mathematics. Experiences of mathematical activities with Trisomy 21 children in Spain have been a main source of inspiration. |
| LÖSTER Tomáš " Simulation of the Behavior of Coefficients for Determining the Number of Clusters in Cluster Analysis " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The main aim of this paper is to compare results of the cluster number determination in using of different clustering methods. To comparison of the behavior of coefficients were used 10 000 generated files, ie it is a simulation of the behavior of selected coefficients in different conditions. On the basis of these analyzes, it can be said, that for data sets where the clusters overlap to 20 % of cluster space, higher success rate is achieved using the Euclidean distance measure. The DB and Dunn coefficient are practically unusable, because their success rate does not exceed 40 %. When using the Euclidean distance measure, CHF and PTS coefficients are more successful. Higher success rate is achieved by the PTS coefficient in combination with the Furthest neighbor method and the average linkage method. The success rate is more than 80 %, which can be considered as a satisfactory value. In conclusion, it is possible to state that the PTS coefficient is the most suitable for finding the number of clusters in the cluster analysis in these conditions. |
| LUKÁČ Stanislav " Preparing Future Mathematics Teachers to Apply Inquiry Approaches to Teaching " - from the section: New Trends in Mathematical Education The official documents for the EU´s education policy emphasize the importance of development of competencies related to innovative teaching and assessment strategies in initial teacher education. Key recommendations for mathematics teaching are focused on learner-centered approach based on inquiry-based learning. Important conditions for successful integration of inquiry approaches to teaching are supplementation of the educational content with examples of inquiry activities and development of teachers´ competencies for application of inquiry approaches to mathematics teaching. The paper describes an inquiry activity to explore and analyse the results of a coin game that could be implemented to the probability teaching in secondary schools. The aim of the proposed inquiry activity is to provide the opportunity for future mathematics teachers to test inquiry work and to use experience for evaluation of the suitability of prepared teaching materials to stimulate students´ engagement in inquiry learning. Future teachers are also required to complete some parts of the teaching materials and to provide suggestions for successful realization of the inquiry activity in mathematics teaching. These partial activities focused on planning and preparing the inquiry activity and its evaluation are intended to inspire future teachers to use different forms of the formative assessment, which should be an important part of the inquiry-based learning. In the conclusion of the paper, we describe the results and the summarized experience received from the realization of the inquiry activity on courses of didactics in daily and external forms of study for future mathematics teachers in the last year of their study. |
| MAGNAGHI-DELFINO Paola " Maria Gaetana Agnesi: Suggestions from the Past to New Way to Teach Calculus " - from the section: New Trends in Mathematical Education In 2018 we celebrated the three hundredth anniversary of the birth of Maria Gaetana Agnesi, mathematician and benefactress born in Milan (Italy). We have examined the Analytical Institutions, the main work of Maria Gaetana, that she dedicated to students education. We think that pre-university students can acquire the fundamental mathematical ideas in Differential Calculus using methods and ideas proposed in the book that go back to the origins of the Analysis. From this point of view, we can use many suggestions and examples, contained in Agnesi’s Books. We can propose these arguments or problems by means of laboratory instruments, flipped classroom techniques, or by didactical methods and we think that the media are different, but the meaning is the same. According to some scholars, the abstract approach, nowadays we use, can be didactically not very effective for the beginner student. They think that an intuition of infinitesimals can be oriented to lead to mathematical concepts. From this point of view, we present the way in which Maria Gaetana Agnesi presented the cycloid, a traditional curve that nearly every mathematician used as example for demonstrating the power of the differential calculus techniques. |
| MALÁ Radka " Design of Experiments in the Laboratory and the Use of Statistical Methods for Data Analysis " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise In the contribution we present application of Design of Experiments on optimization of chromic salt adsorption on sheep wool. Using four factors involving time and contact manner of the wool with adsorbate solution, the solution concentration and pH as well as ratio of the solution volume to wool mass, all at two levels, optimal conditions for the adsorption experiments were found. Application of those conditions can accelerate research. |
| MALACKÁ Zuzana " A Behavioural Car-Following Model and Solving the Quick Thinking Driver Model " - from the section: Differential Equations, Dynamic Systems and Their Applications A simple mathematical model for how individual vehicles follow each other along a stretch of road is discussed. The ability to predict to response a vehicle in a stream of traffic to the behavior of its predecessor is important in estimating what effect changes to the driving environment with have on traffic flow. Various models proposed to explain this behavior have different strengths and weakness. In this paper we discuss a car following model and its results in a second-order or first-order ordinary differential equation. The resulting can be used as a motivator to encourage students to think critically about the physical interpretation of the results that the equation produces. |
| MARCINEK Milan " Fire Units in Slovakia: Analysis of Outgoings " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The aim of the article is finding the basic statistical characteristics for fire brigade operations within the Slovak Republic. According to the law, Fire and Rescue Service is obliged to present information related to its activities annually through statistical yearbooks of the Ministry of the Interior of the Slovak Republic. The total number of fire brigade outgoings in 2017 was 33672. In Slovakia, we have used five classes of outgoings. Classification of outgoings on technical assistance, fire, traffic accidents, and splitting of dangerous substance is provided. The study of outgoings of fire service units has been realized in the municipalities of the Slovak Republic. Numerical studies have shown how the number of fire unit outgoings and times of their durations have changed in different regions, different months and different days.Using regression analysis the number of outgoings will be explained by population in the region, using the area of the region, using population density. |
| MAREK Patrice " Sports Betting Arbitrage in English Football " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The paper investigates sports betting arbitrage and demonstrates it on data from English football between seasons 2013–14 and 2017–18. Several strategies of arbitrage betting are proposed, e.g., preference for favourite or outsider, and they are used for betting in four top level English football leagues. Results are compared using average profit per match, and, as can be expected, best values are obtained for the Premier League with 110 arbitrage opportunities in the 2017–18 season. |
| MAREK Jaroslav " Testing of Birkhoff Hypothesis from Mathematical Aesthetic " - from the section: Mathematics and Art The paper is part of a broader study to verify some hypotheses about the relationship between aesthetic characteristics of an image and the emotions that this image provokes. Here we will go through a survey where respondents would communicate their emotions. The main objective is to study dependency of viewing emotions on aesthetic characteristics. |
| MATVEJEVS Andrejs " Stochastic Approximation of the Logistic System Dynamics " - from the section: Differential Equations, Dynamic Systems and Their Applications The stochastic dynamic of logistic system problem addresses the movement of vehicles between their locations over a given planning horizon. This problem deals with a logistic system consisting of a wholesale store, a retail store and automobiles which are taking part in goods delivery from a wholesale store to a retail store. Assuming the demands are random and coming at random time moments, we construct a stochastic model for this transport logistic scheme and derive Gaussian approximation for transport and stock level of goods dynamics. |
| MATVEJEVS Aleksandrs " New Practical Methods of Analysis of 2nd Order Curves on a Plane " - from the section: New Trends in Mathematical Education In this work second order curves have been studied in all their diversity as they appear in applications. These curves have been examined without using the concept of rotation, a concept which is introduced artificially in textbooks in order to simplify the basic form of the canonical equations of these curves: a concept which is only used for inclined second order curves, and which is both intimidating and difficult for newly accepted university students. A new, methodological approach, based only on completing the perfect square, has been proposed, and “generalized” formulas of equations for an ellipse, a hyperbola and a parabola have been obtained. The use of these formulas has been shown in particular examples of the study of several inclined second order curves, analyzing their basic characteristics and graphing. The new generalized formulas of ellipse and hyperbola equations seem absent in literature. |
| MELE Giampiero " Geometry and Design Artworks’ Reconstruction New Methods or New Tool? " - from the section: Mathematics and Art Descriptive geometry is the science that Gaspard Monge systematized in 1794 and that was widely developed in Europe, up until the first decades of the twentieth century. The main purpose of this science is the certain and accurate representation of three-dimensional shapes on the two-dimensional support of the drawing, using successive auxiliary views. This method uses quantitative measures of length, angles, shapes and other geometric information. The technology required a systematic approach to problem solving with accuracy in projections and transfer of distances from previous views. The layout and position of the successive auxiliary views were essential in the solution of the problem. Descriptive geometry has been the object of theoretical studies, and is an essential tool for designers, engineers and architects. Nevertheless, at the end of the last century, the availability of electronic machines capable of representing three-dimensional shapes has produced an epochal change, because designers have adopted the new digital techniques almost exclusively. Apparently, in architectural practices, CAD (Computer Aided Design) has replaced descriptive geometry as a tool for the representation and in Universities, the teaching of descriptive geometry is disappearing. Today, the users of computer graphics do few or none relation between the CAD’s tools and descriptive geometry. The purpose of this paper is to show by examples that the concepts of descriptive geometry have not changed, only the process through which we obtain the results has changed. On this purpose we study the design of the armchair prototype designed by Augusto Magnaghi-Delfino in 50’s. |
| MERCAT Christian " Diffusion of Mathematics Using Interactive Art with Webcams " - from the section: Mathematics and Art Diffusion of Mathematics Using Interactive Art with Webcams Generative art has been around for quite a while and limited interactivity such as motion sensors, knobs or buttons, but only recently rich direct interactivity has been widely used by artists for example Adrien M. and Claire B. http://am-cb.net in Lyon. Every such interactive art uses of course a lot of mathematics, which is apparent to the trained eye, but it is not the purpose of these art works. On the other hand, mathematical dissemination usually relies on a « content first » approach that requires intellectual involvement, from the start, to just begin grasping the ideas. Therefore the mathematics that are shown in science fairs are usually either cultural, elementary or restricted to an elite audience. This talk will be a case for a hybrid strategy, between art and mathematics, showing advanced mathematics as a pictural process, involving audience through their interaction with the device, with the aim to bait them into questioning the mathematics behind this pictures. Before understanding the concepts, these installations will act as visual anchors for far fetched notions such as « differential equations », « conformal mapping », « four-dimensional projection » and, through involving own´s picture and own´s gestures, add a personal experience to already pictorial notions such as « function graph », « iterated function system » or « Julia set ». List of already existing webcam, a joint work with Aaron Montag, PhD student in TU-München https://www-m10.ma.tum.de/bin/view/Lehrstuhl/AaronMontag http://bit.ly/Anamorphose http://bit.ly/HommeArbre http://bit.ly/webcamconf http://bit.ly/TaylorWebcam http://bit.ly/JuliaWebcam http://bit.ly/SierpinskiWebcam http://bit.ly/WebcamSliced https://montaga.github.io/droste/ |
| MICULESCU Radu " Iterated Function Systems Consisting of Continuous Functions Satisfying Banach´s orbital " - from the section: Differential Equations, Dynamic Systems and Their Applications We introduce the concept of iterated function system consisting of continuous functions satisfying Banach´s orbital condition and prove that the fractal operator associated to such a system is weakly Picard. Some examples are provided. |
| MIKEŠ Josef " On Fundamental Equations of Rotary Vector Fields " - from the section: Algebra and Geometry and Their Applications In presented paper we study rotary vector fields in two-dimensional (pseudo-) Riemannian spaces, which admit rotary mappings. These spaces do not have to be isometric to surfaces of revolution. We obtained fundamental equations in the Cauchy type form, which depends on no more than 3 real parameters. |
| MILLAN GASCA Ana " The Role of the Stage Presence in Primary Mathematics Teachers Education " - from the section: New Trends in Mathematical Education Extended abstract The aim of this research is to cope with the expression challenge regarding the embodiment of mathematical ideas in primary teachers´ professional activity in the classroom. Our guess was that 20th century´s approaches and technical contributions to actors and dancers training by Rudolf Laban (1879-1958), Émile-Jacques Delcroze (1865-1950) and Eugenio Barba (b. 1936) could be applied to the design of a specific math teachers dramatizing training (Laban 1948, 1971, Dalcroze 1921, Barba 1991). Starting in late 2012, theoretical research has been carried on along with the design, implementation and assessment of workshops with pre-service students (degree in Primary Education) and with in-service teachers. We discuss the theoretical framework, regarding 20th performance training, together with relevant mentions of the role of stage presence in the teaching of mathematics by two mathematicians and outstanding scholars in mathematics education, the Italian Federigo Enriques (1871-1946) and the Hungarian born American George Polya (1887-1985). The pedagogical aspects of mimesis, ´´a link between what is expressed and what really is´´ (Scaramuzzo 2010, 2013, 2016) were also considered, regarding both mathematics teachers education and professional development and pupil´s learning of mathematics in preschool and primary school. We then considered the structure of 3-4 hours sessions and 16 hours workshops; the different exercises, regarding sight, motion in the space (the classroom); the accompanying writing (personal notebooks or zibaldoni). We discussed our qualitative methodology in assessment (Van Manen 1990), the main results, and future research perspectives. |
| MINCULETE Nicusor " About Linear Regression for Two Independent Variables " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The linear regression plays a very important role in the analysis of a discrete random variable in finite case. In the present paper we will obtain several characterizations of the linear regression for two independent discrete random variables in finite case. |
| NÁHLÍK Tomáš " 3D Reconstruction and Volume Measurement of Microscopic Images Using MATLAB " - from the section: Modeling and Simulation in Engineering and Scientific Computations This paper is devoted to modern trends in image analysis. 3D reconstruction is necessary for knowing the shape and due to volume calculation the different treatment of biology material can quantified. |
| NENKA Ruslana " Almost Geodesic Mappings of the Second Type of Spaces With Affine Connection onto Two-Symmetric Spaces " - from the section: Algebra and Geometry and Their Applications In the paper we consider canonical almost geodesic mappings of the second type of spaces with affine connection onto two-symmetric spaces. The main equations for the mappings are obtained as a closed mixed system of PDEs of Cauchy type. We have found the maximum number of essential parameters which the solution of the system depends on. |
| NERI MACCHIAVERNA Francesca " The Role of the Stage Presence in Primary Mathematics Teachers Education " - from the section: New Trends in Mathematical Education The aim of this research is to cope with the expression challenge regarding the embodiment of mathematical ideas in primary teachers´ professional activity in the classroom (Lakof, Núñez 2000). Our guess was that 20th century´s approaches and technical contributions to actors and dancers training could be applied to the design of a specific math teachers dramatizing training. We discuss the design, implementation and assessment of exercises in workshops with pre-service and in-service teachers. |
| NORANDO Tullia " Maria Gaetana Agnesi: Suggestions from the Past to New Way to Teach Calculus " - from the section: New Trends in Mathematical Education In 2018 we celebrated the three hundredth anniversary of the birth of Maria Gaetana Agnesi, mathematician and benefactress born in Milan (Italy). We have examined the Analytical Institutions, the main work of Maria Gaetana, that she dedicated to students education. We think that pre-university students can acquire the fundamental mathematical ideas in Differential Calculus using methods and ideas proposed in the books that go back to the origins of the Analysis. From this point of view, we can use many suggestions and examples contained in Agnesi’s Books. We can propose these arguments or problems by means of laboratory instruments, flipped classroom techniques or by other didactical methods and we think that if the media are different, the meaning is the same. According to some scholars, the abstract approach, nowadays we use, can be didactically not very effective for the beginner students. Teachers think that the intuition of infinitesimals can be oriented to lead to mathematical concepts. From this point of view, we present the way in which Maria Gaetana Agnesi presented the cycloid, a traditional curve that nearly every mathematician used as example for demonstrating the power of the differential calculus techniques. |
| ORSZÁGHOVÁ Dana " Comparative Assessment of Factors Determining the Decision-Making of Respondents " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The consumers’ behaviour in the decision-making has a great dynamics since it is influenced by many factors such as experience, information, advertising, financial income, and others. As a result of the decision during the purchase of goods and services, it is either the realization of the purchase or the postponement or the rejection of the purchase. The main objective of this paper was the assessment of factors determining the decision-making of respondents. Milk and dairy products belong to the frequently purchased goods because they contain the important components for a human nutrition. Data on the purchase and consumption of milk and dairy products were obtained through a questionnaire survey. The statistical sample was focused on the students of the Faculty of Economics and Management at the Slovak University of Agriculture in Nitra. The respondents should determine the importance of each criterion as they take into account when purchasing milk and dairy products. Then we wanted to identify the order of the importance for these selected criteria: price, quality, mark, appearance, taste quality, health effects and durability of a product. Using the estimation methods for weights of criteria (method of order and point’s method) it was found, that the most important criterion is the quality of the product, followed by the taste properties of the product, and the price of the product is the third most important criterion. The respondents consider the appearance of a purchased product as the least important criterion. |
| OTAVOVÁ Miroslava " Association between Score from Mid-term Test and Final Grade (co-author I. Sýkorová) " - from the section: The aim of this paper is to analyse the impact of score from mid-term test on the final grade in mathematics. A contingency table is used for analysing the relationship between the scores from mid-term test and final grades. Firstly, descriptive statistics and graphs for both variables are given and then contingency tables are presented. The association measures turn out to be highly significant and therefore the use of the results for students’ motivation is discussed. |
| PACURAR Cristina Maria " Pablo Picasso and Bézier curves " - from the section: Mathematics and Art The present paper is composed of two parts. The first part aims to reproduce some famous line drawings of Picasso using Bézier curves, while the second part is an exercise of the inverse process, of finding the hidden subject behind paintings. |
| PAJEROVÁ Nikola " Similarity of Triangular Meshes Measurement " - from the section: Algebra and Geometry and Their Applications he need to measure a similarity between two 3D objects belongs to highly challenging problems in computer graphics. In this paper, shape distributions approach based on three different shape functions is used to compute a similarity measure of triangular meshes. The evaluation is based on a measurement system analysis (MSA), a statistical method commonly used in quality management systems. MSA is defined as an experimental and statistical method to identify the sources of variation in a measurement process and determine the value of these variations. Based on calculation of variance range of measurement repeated several times, it is possible to assess statistical competence or incompetence of the most important variation sources. In this paper, the MSA approach is modified, so that the capability of three different shape distributions to calculate similarity measure of triangular meshes is assessed. Shape functions that measure simple geometrical features on a 3D model are used in shape distributions approach to simplify solution of shape matching problem. If the shape distributions are used, two probability distributions sampled from a suitable shape function are compared instead of traditional shape matching methods. The triangular meshes were obtained by repeated optical scanning of the same object by means of three different scanners. To compare the shape distributions of the scanned meshes with a suitable reference data, the shape distribution of the nominal mesh generated on the theoretical CAD model of the scanned object was created, the Minkowski L1 norm was calculated and all obtained values were analysed by MSA. |
| PASÁČKOVÁ Jana " Analysis of Students of the Study Programme Travel and Tourism and Their Mathematical Skills " - from the section: New Trends in Mathematical Education The paper discusses the results of the test from mathematics at the College of Polytechnics Jihlava. The aim is focused on the differences between the scores of students of different secondary schools and in addition, we observe the effect of the prepare activities of our college on test results. |
| PASÁČKOVÁ Jana " Oscillation Theorems for Difference Equations of the Fourth Order " - from the section: Differential Equations, Dynamic Systems and Their Applications We investigate a difference equation of the fourth order. We state the condition for the nonexistence of quickly oscillatory solutions. We define the possible types of nonoscillatory solutions and we present an oscillation theorem. |
| PAUN Marius " Thousands Years in History, One Hundred Years of Modern Romania. Landmarks in Cultural Heritage. " - from the section: Mathematics and Art The Thinker of Hamanghia; Pottery of Cucuteni; The Tablets of Tartaria; The Gods Zamolxes, Gebeleizis, Bendis; Sarmizegetusa Regia; Tropheum Traiani in Adamclisi; The Martirion; The Voivodal Church and the Monastery in Curtea de Arges; the colors of Bucovina; Sapanta; Cumintenia Pamantului. A complete helix arc in our culture. |
| PAVLENKO Oksana " Stochastic Modeling for Age Structured Population Growth under Assumption of Small Fast Oscillating Perturbations " - from the section: Differential Equations, Dynamic Systems and Their Applications We analyse Markov impulsive difference model for age structured population divided into three groups under assumption of perturbations at random time moments. Assuming sufficiently small intervals between changes, we apply the stochastic averaging procedure and construct an ordinary 3-dimensional differential equation for population dynamics in the mean and a linear 3-dimensional stochastic differential equation for deviations from the mean trajectories. The results are applied for modelling of population dynamics using the data about Latvian residents collected by the Central Statistical Bureau of Latvia. |
| PIRKLOVÁ Petra " Metric Problems in Monge Projection in GeoGebra " - from the section: New Trends in Mathematical Education Monge projection and particularly metric problems of Monge projection are very demanding in terms of spatial imagination. Therefore, it is suitable to apply the dynamic applets in geometric software GeoGebra in the lessons of descriptive geometry. The above mentioned 3D applets are highly practical as they provide a better spatial imagination. |
| PODOUSOVA Tatyana " Special Deformations of Hypersurfaces of Riemannian Spaces " - from the section: Algebra and Geometry and Their Applications In the present paper we consider infinitesimal deformations of a pseudo-Riemannian space which map each geodesic to a curve approximating a geodesic with given precision. This approach seems to be more appropriate for applications than the standard one, for example, for simulating real physical situation when evolution of gravity fields, electromagnetic fields, mechanical systems is considered. |
| PORUBA Jakub " Construction of Special 3D Models for Monge Projection " - from the section: New Trends in Mathematical Education At secondary schools and universities, students meet different types of projections in courses on descriptive and constructional geometry. Monge projection is included as a part of basic projective methods, however it is not trivial issue. Main problem is that students have problems with imagining the given situation they are to solve and thus they cannot identify themselves with the task. The aim of this contrubution is to introduce models that can be used in teaching of the Monge projection and to describe the method of their creation. |
| POSPÍŠIL Jiří " Space-Time Theory of Retail Gravitation in Economics of Sun-Earth Relationships " - from the section: Nothing This paper is dealing with space-time theory of retail gravitation in economics of Sun-Earth Relationships. The mathematical model for physical space-time with the field of retail gravitation is based on a four-dimensional differentiable manifold on which is defined a symmetric covariant second-order tensor field, i.e. metric tensor, having Lorentzian signature. (Coauthor of the paper: Ing. Tomáš R. ZEITHAMER, Ph.D., University of Economics, Prague, Czech Republic) |
| POTŮČEK Radovan " The Sum of the Series of Reciprocals of the Cubic Polynomials with Triple and Double Zero Root " - from the section: Modeling and Simulation in Engineering and Scientific Computations This contribution is a follow-up to author´s papers (1) and (2) dealing with the sum of the series of reciprocals of the quadratic polynomials with double non-positive integer root and with the sum of the series of reciprocals of the cubic polynomials with three different positive integer roots. We deal with the sum of the series of reciprocals of the cubic polynomials with triple zero root and with double zero root and one non-zero integer root. We remember the well-known formula for the sum of the case of triple zero root and derive two formulas for the sums of the case of double zero root both with negative and with positive integer root and verify them by some examples evaluated using the basic programming language of the computer algebra system Maple 16. This contribution can be an inspiration for teachers of mathematics who are teaching the topic Infinite series or as a subject matter for work with talented students. |
| POZDÍLKOVÁ Alena " Monday Effect on Stock Prices: Testing of Statistical Hypothesis " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The aim of this article will be to analyse one of calendar effects - Monday effect. In testing, we will not just go through analysing price returns, but we will study the values of the measurement of investment success. Therefore, we will determine the Win Ratio, Profit Factor, and Profit Loss Ratio. For hypothesis testing, we suggest appropriate statistical tests. We will work with the prices of the period from January 2005 to October 2018 for 29 stock companies that are part of the DJA index. |
| PRÁŠILOVÁ Monika " Active Learning Methods in Engineering Mathematics - Adventure and Challenge " - from the section: New Trends in Mathematical Education Paper brings information on experience with introduction of innovative active learning and teaching methods into basic course Mathematics I for the first year engineering students at the faculty of Mechanical Engineering, Slovak University of Technology in Bratislava, Slovakia. Evaluation of experiment results and students achievements is presented in statistical data. Supplementary analysis of feedback obtained from students in questionnaire shows insight into students opinions on various teaching scenarios and comparison of used methods of eduScrum and individual study. |
| PRAZAK Pavel " Customer´s Selection of Mobile Phone Tariff " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise Managers and their decisions can be successful only if they work with correct and relevant information. Because it is not possible to implement an experiment with institutions that are to be managed, it is necessary to provide artificial experiments within an appropriate model. This is the way how simulation models are introduced into managerial work. The aim of this paper is to introduce a simulation model and its implementation in MATLAB that can be used for estimation of total monthly cost for a selected mobile phone tariff. Finally the properties for different parameters and other tariffs are discussed as well. |
| RIHA David " Factor Analysis in Classifying Personal Sales Factors in Automotive Industry. Switzerland Case " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise Factor Analysis is an exploratory technique applied to a set of observed variables that seeks to find underlying factors from which the observed variables are generated. The following paper discusses exploratory factor analysis and provides us a basics of this technique and describes how it can be used in research designs with following applications on personal sales process. Mathematical aspects of factor analysis are described and explored for better understanding, how the factor analysis works in practice. In finally section of the following paper provide how to write up the results of the factor analysis, how to interpret tables and graphs in output, in other words, directly to practise. |
| RIHOVA Elena " Comparison New Quality Indices for Fuzzy C-Means Clustering " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise Factor Analysis is an exploratory technique applied to a set of observed variables that seeks to find underlying factors from which the observed variables are generated. The following paper discusses exploratory factor analysis and provides us a basics of this technique and describes how it can be used in research designs with following applications on personal sales process. Mathematical aspects of factor analysis are described and explored for better understanding, how the factor analysis works in practice. In finally section of the following paper provide how to write up the results of the factor analysis, how to interpret tables and graphs in output, in other words, directly to practise. |
| ŘÍHOVÁ Dana " Several Products of Financial Mathematics as Linear Difference Equations " - from the section: Financial and Actuary Mathematics This paper focuses on applications of linear difference equations of the first order in the field of finance. The values of financial products are given as a sequence of values observed at discrete time intervals and a number of models can be expressed by the recursion between two consecutive elements of the sequence where the initial value of the first element is given. The formulas used in finance represent the rule for calculating the n-th element of such a sequence and are usually derived from the recurrence using the properties of a geometric sequence, especially the sum of a geometric sequence. But this recursive rule constitutes a difference equation which is linear of the first order with constant coefficients. The initial condition is usually given by the first element of the sequence. To find the functional notation for the n-th element of the above sequence means to solve the appropriate difference equation. In this contribution a basic linear difference equation of the first order appearing in financial mathematics is presented and its general solution is derived. It is shown that this solution represents an universal formula for calculating some financial products. Using this solution we express appropriate formulas of finance, namely compound interest, the future value of annuities due and ordinary annuities called long-term savings, the present value of annuities due and ordinary annuities referred to as rents and finally loan amortization. Consequently we have obtained important formulas occurring in finance by means of applying the solution of difference equation without using the properties of a geometric sequence which is common. |
| RODKINA Alexandra " Preserving Positivity in Solutions of Stochastic Delay Difference Equations " - from the section: Differential Equations, Dynamic Systems and Their Applications We discuss positivity on a compact interval of solutions of stochastic delay difference equations which can be treated as an Euler discretization of stochastic delay It^{o} differential equation. Positivity with arbitrarily high probability is observed as the number of mesh points deployed grows large. In addition, a useful a priori estimate of the number of mesh points required to achieve positivity with fixed probability is derived. |
| RUMANOVÁ Lucia " Design of Non – Routine Problems in Training of Future Primary School Teachers with Emphasion on Application " - from the section: New Trends in Mathematical Education The primary school students have a lot of knowledge of mathematics which they need to understand and employ in their future daily live. The standard tasks usually support the below cognitive skills. Unlike them, the non-standard tasks are helpful to gain the informal knowledge and approximate mathematics to the pupils´ needs. In the contribution we introduce experiences of future primary school teacher with creation and inclusion of the some non-standard tasks in educational process. |
| SALVADORI Anna " Digital Photagraphy Math Replaced the Dark Room " - from the section: New Trends in Mathematical Education The new generations, always connected to internet, are immersed in a virtual world made of images. They make massive use of digital images that even replace words in their communications. But they often do not know anything about the nature of digital photography, nor are they aware of the importance of mathematics in the creation and management of the photos. This note is just a short essay to show how much elementary mathematics is hidden behind digital images. We do hope also to offer to the teacher an excellent opportunity to reconnect the traumatized by mathematics. |
| SÁRKÖZI Réka " Correlation betwen the Static Behaviour of Dome Structures and their Graph Characteristics " - from the section: Algebra and Geometry and Their Applications In this research the graph characteristics of dome structures and their effect on the structural behaviour were analysed. Graph theory is a branch of mathematics which is useful in many fields of science. Graph characteristics can tell a lot about the behaviour of complex systems. The graph representation of different type of single layer Schwedler, ribbed, lamella and diamatic domes were analysed and the results shows that the average degree and the average clustering coefficient of them have a great impact on the structural behaviour of the dome structure. |
| SAVCHENKO Aleksandr " On the Conformal Mappings of Special Quasi-Einstein Spaces " - from the section: Algebra and Geometry and Their Applications We have studied the conformal mappings of special quasi-Einstein spaces. We have proved that they are closed with respect to concircular mappings. We have introduced the notion of mobility of pseudo-Riemannian spaces with respect to concircular mappings. The tensor characteristic of maximal mobility for special quasi-Einstein spaces has also been found. |
| SCHREIBEROVA Petra " Geometrical Meaning of Derivatives in GeoGebra " - from the section: New Trends in Mathematical Education The aim of the paper is to present teaching procedure based on the 3D module in GeoGebra. We regularly use GeoGebra during education of mathematics at university level. We would like to show connection and cooperation between the teacher, students and GeoGebra. It could be interesting for teachers and their future methodology of teaching. We present the GeoGebra approach for one topic from the chapter "Differential Calculus of Functions Depending on Two Real Variables", especially explanation of the geometrical meaning of partial derivatives. |
| SEDIVA Blanka " Risk Events for Two Random Processes " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The problem when a random variable exceeds some boundary is very often studied problem in many fields of science. The classical approach focuses on situation when random variable overlap a fix value. More general methods interested in situation with two random variables and the risk events occurs when the value of one random variable exceeds the value of the second random variable. This paper deals with a problem of exceeding for two random which are analysed in time. For two correlated random normal processes with systematically trend parts are studied statistical properties of their difference and statistical properties of cumulative variables. Although assumptions of models do not necessary correspond with the reality, the application of the real data show a possible application of this approach. |
| ŠIMPACH Ondřej " Using DEA to Assess the Differences in Technical Efficiency Between Farms Managed by Young and Other Farmers " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The aim of the paper is to assess the differences in technical efficiency between farms that are managed by young farmers (under 40 years) and other farmers using DEA. CCR and BCC input-oriented models are calculated and compared. Farms owned by young farmers are efficient from 54.2% and others from 51.6%. Average scale efficiency is also higher in case of young farmers. They have increasing returns to scale more often. The test reveals that the differences are statistically insignificant. |
| SISÁKOVÁ Andrea " CLIL Approach in Mathematics " - from the section: New Trends in Mathematical Education An interest to use new methods and forms within Mathematical education is constantly growing. As well as the knowledge of at least two foreign languages which is considered as one of the priority skill by European Union. CLIL (Content and Language Integrated Learning) approach is a possible solution for both demands. Regarding to this our aim is to create educational materials that would improve teaching Mathematics in English language using CLIL approach at Slovak schools |
| ŠLESAR Peter " " - from the section: The work is devoted to the analysis of the type worm drives using the stress-strain analysis in the ANSYS Workbench. The work is logically divided into a several parts. The first section briefly describes the use of the worm drives and said their basic advantages in terms of mechanical engineering. Then are presented the facts bearing on the calculation of the worm drives and the slewing rings. Another part of the work is devoted to calculation of the worm drives of the turn based on the Hertz theory of contact pressures. In terms of efficiency of the worm drives, the surface treatment is also important. Based on the distribution and depth of the maximum shear stresses below the surface, the required thickness of the cementation layer of the outer and inner rings is determined |
| SLOVAK Juraj " Position Estimation of the Mobile Robot Using the Kalman Filter " - from the section: Mathematics and Physics in Contemporary Science and Technique The paper presents need of using Kalman filtering to optimize location of mobile robotic systems and more accurate navigation. Theoretical knowledge was verified on real system represented by mobile robotic system (MRS) with mecanum wheel. Construction deficiencies causes large deviations in movement from desired trajectory, which makes using Kalman filter more efficient. Localization was performed in indoor hall using odometry from motion sensors and tracking landmarks placed on the hall ceiling with infrared camera Stargazer. On obtained data was used discrete KF, subsequently modified data were used to regulate motion. Acquired motion trajectories were compared at the end of the article. |
| SMETANA Bedřich " Model of Iterated Artificial Neurons " - from the section: Algebra and Geometry and Their Applications Application of algebraic structures in research of structure of the most used artificial neural network - multilayer perceptron and functionality of artificial neuron, is one from current the most interesting areas in the usage of time varying artificial neurons. In this paper, we have described certain properties of constructed algebraic structures of artificial neurons, including the hypergroup formed by iterated models of artificial neurons. By using an analogous approach, a fresh look at the structures of artificial neurons is used here. |
| SMETANOVÁ Dana " Regular Hamiltonian Systems and Its Projectability " - from the section: Algebra and Geometry and Their Applications Lepagean (n+1)-forms corresponding to second order Lagrangians are studied. The projectability and regularity conditions of Hamiltonian systems are presented. |
| ŠOVČÍKOVÁ Petronela " Teaching and Learning Analytic Geometry with Technology " - from the section: New Trends in Mathematical Education Technology can play an important role in mathematics education. In this paper we focus on using ICT in teaching and learning analytic geometry at grammar school. Our research was realized in two classes – the first class was control group and the second one was experimental group. There were 50 pupils (26 pupils in the first class and the 24 pupils in the second class). The main aim of this research was to verify our hypothesis: Can pupils accomplish better results when they are taught and learned analytic geometry with technology? In this study materials have been prepared to pupils from experimental group in learning environments. Pupils were able to form correct concept images related to mathematical expressions or problems. This study shows that dynamic software has a positive impact on students´ achievement in the topic Analytic geometry. The students have also positive perceptions on software in terms of enthusiasm, confidence and motivation. |
| STANGANELLI Anna Maria " Some Remarks on the 3-th Hypersimplex and Applications " - from the section: Algebra and Geometry and Their Applications The r-th hypersimplex, r>=2 is defined as the set A of lattices points of N^n, N the semigroup of natural numbers, whose coordinates are (i1,i2,…,in), with i1+i2+⋯+in=r, and it in {0,1}, 1 <=t<=n. For r=2 the second hypersimplex is studied by Sturmfels in Groebner bases and convex polytopes, Univ.Lectures Series, Amer.Math.Soc.,Vol.8,(1995). For r>2, the situation is different. The sorted Groebner basis of its toric ideal I consists of binomials of degree two, but both lexicographic and reverse lexicographic Groebner bases are in general not quadratic. Since the most popular term orders are twofold, the lex (reverse) lexicographic orders, we are interested to establish lower and upper bounds for these bases, since the triangulations associated can be more interesting in different fields, in particular from the geometric point of view. For n=6 is proved by Sturmfels that the Groebner basis of the toric ideeal of I, with respect to the sorted order, isn´t lexico graphic neither reverse lexicographic, that means that I admits a lexicographic or reverse lexicographic Groebner basis of degree >2, for all orders of the variables. As a consequence, an open problem is to found a bound for the degree of the both lexicographic and reverse lexicographic Groebner bases of I, for n>6. The aim of this paper is to extend the result of Sturmfels to the case n>6. We prove that I, n > 6 admits a quadratic sorted basis that is not lexicographic neither reverse lexicographic, of degree >= 5 Some remarks about sorted triangulations of the 3-th hypersimplex imo are given. |
| STANGANELLI Anna Maria " The Buchberger Graph of Some Classes of Polytopes " - from the section: Algebra and Geometry and Their Applications The staircase diagrams in bidimensional and three- dimensional cases, were introduced by E.Miller and B. Sturmfels in Combinatorial Commutative Algebra, Springer GTM 227(2004). The reason was that these geometric objects arise from monomial ideals that, for a combinatorial point of view, are more easy ti manage that in general case (ideals generated by polynomials). They are recently utilized in order to solve security problems, as reserved paths, reserved building and places of targets. To achieve one’s rapidly, the set of data we would to transmit has to be the smallest possibile, than we have to individualize classes of monomial ideals for which the objective is reached. In this paper we consider the class of principal Borel ideals generated only by a monomial ( the Borel generator), and the class of principal Borel polytopes. |
| STAŠ Michal " Determining Crossing Number of One Graph of Order Five Using Cyclic Permutations " - from the section: Algebra and Geometry and Their Applications The main aim of the paper is to give the crossing number of join product G+D_n for the connected graph G of order five consisting of one vertex incident with one leaf of the complete bipartite graph K_{1,3}, and D_n consists on n isolated vertices. In the proofs, it will be used an idea of new representation of the minimum numbers of crossings between two different subgraphs which do not cross the edges of the graph G by the graph of configurations in the considered drawing D of G+D_n. Moreover, we extend also known results concerning crossing numbers for join products of the graph G with the path P_n and the cycle C_n on n vertices. |
| SÝKOROVÁ Irena " Association between Score from Mid-term Test and Final Grade (co-author M. Otavová) " - from the section: The aim of this paper is to analyse the impact of score from mid-term test on the final grade in mathematics. A contingency table is used for analysing the relationship between the scores from mid-term test and final grades. Firstly, descriptive statistics and graphs for both variables are given and then contingency tables are presented. The association measures turn out to be highly significant and therefore the use of the results for students’ motivation is discussed. |
| SZABÓ Tibor " Some Remarks on Number Theory in High School Education " - from the section: New Trends in Mathematical Education In our paper we are trying to show possibility of applying of some university curricula in the field of number theory into high school education. Current approaches use recent knowledge which leads to new effective methods and theories, but our approach is based on history of number theory. We think about Euler’s Totient function and Fermat’s little theorem with regards to properties of divisibility. In our consideration students can understand inclusion-exclusion formula. Such mathematical content is appropriate mainly for talented students. |
| SZILASSI Lajos " Dynamic Visualization of Hyperbolic Geometry in the Poincaré Disk Model " - from the section: New Trends in Mathematical Education In a letter to his father, Bolyai wrote in 1823: “out of nothing I have created a strange new universe.” This new universe is demonstrated in [1], an electronic GeoGebra book that makes the basics of hyperbolic geometry easy to understand and visually clear. Even more important aim is to sketch up a new perspective for some well-known Euclidean notions and constructions. Most of the problems discussed in this paper do not use the Euclidean axiom of parallels. |
| TAN SHILONG " Impossible Spaces Through Virtual Reality " - from the section: Mathematics and Art Focusing on the links between space and image, this paper aims at investigating some visual aspects of the so called ‘impossible spaces’, taking advantage of virtual reality. Starting from a series of works of Maurits Cornelis Escher, a three dimensional version of a selected example will be presented, visualized, and explored with the help of VR, in order to detect the relevant projective characters making the illusion possible. |
| TEDESCHINI-LALLI Laura " A Metallic 1928 Geodesic Dome in Rome " - from the section: Mathematics and Art In Rome a metallic geodesic dome (1928) is still visible in its structure, sheltered in the large Octagonal Hall of the imperial baths of Diocletianus. The first geodesic dome ever built, in Jena (1926), is not visible any more, therefore the roman one is probably the eldest existing geodesic dome. Both the one in Jena and that in Rome are metallic grids and were planned to support a (spherical) screen for a planetarium. To argue it deserves the attribute “geodesic” we performed a first onfield topological survey concerning the vertex degrees. |
| TOMICZEK Petr " Second Order Problem with a Symmetric Nonlinearity " - from the section: Differential Equations, Dynamic Systems and Their Applications The purpose of this work is to study the existence of a solution to the nonlinear second order ordinary differential equation u´(x) + m^2 u(x) + g(x,u) = f(x), x in [0, T], u(0) = u(pi) = 0, where m in N, g is a Carathéodory function, f in L^1(0,pi), a quotient g(x,s)/s lies between -2m + 1 and 2m + 1. The technique we use is the saddle point theorem. |
| TOMICZKOVA Svetlana " Motivation of a Student in Geometry Courses at the Faculty of Mechanical Engineering " - from the section: New Trends in Mathematical Education Students often ask what theoretical subjects will teach them for their future careers. It is advisable to show real problems during their courses which are solved by experts in practice or doctoral students. One such problem is the sharpening of a hobbing worm milling cutter. Theoretical foundations from the geometry course have been used to solve this problem. |
| ŤOUPAL Tomáš " Nonparametric Kernel Regression Approach " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise This paper is focused on a possible methodology for estimating of regression curve by nonparametric kernel regression approach. The main objective is a description of nonparametric regression function with using Nadaraya-Watson approach including a real data application for beer consumption in the Czech Republic and the Slovak Republic. It includes the influence of the basic parameters and proposal some appropriate optimization methods. It means a calibration of the proposed model. |
| TREMATERRA Amelia " The Effects of the Harmonic Choir Stalls on the Acoustics of the Church of the Certosa of San Martino in Naples " - from the section: Mathematics and Art e Church of the Certosa di San Martino (Naples) was built in the XXVI century and is characterized by the presence of an elliptical harmonic box built under the floor of the choir. The harmonic box was designed to resolve the effects of the weakening of the chants following the opening of some large windows. This paper presents the results of acoustic measurements carried out in the church to evaluate the effects of the presence of the sound box. There was a variation in the acoustic parameters at low frequencies in only the area of the choir. |
| VACKOVÁ Jana " The Microscopic Analysis of Velocity-Density Paradigm " - from the section: Statistical Methods in Technical and Economic Sciences and in Practise The relation between density and velocity is one of the most crucial aspects of pedestrian movement. Although some mechanisms are considered to be general true, our research on this topic finds some limits. Firstly, the general density distribution concept focused on the individual density is presented - each pedestrian is considered as the source of conic density distribution. When the density is set, velocity-density correlation is evaluated using the data from egress experiments realized by our research group in the last years and surprising behavior is measured for the dense crowd near the exit which disables to predict pedestrian velocity by density. Thus, follower-leader model using velocity of leaders to predict the motion of followers is developed and presents a good complement to velocity–density relation. |
| VÁCLAVÍKOVÁ Zuzana " Maths for Non-Maths Students " - from the section: New Trends in Mathematical Education The article outlines the differences that occur in the teaching of mathematical subjects with regard to whether they are taught for mathematics students or for students of non-mathematical disciplines. Our experience and suggestions for improving the motivation of both sets of students are presented through the use of mathematics linked to their area of study and relevant word problems. |
| VÁGOVÁ Renáta " Plane, Physical or Dynamic Representations of 3D Objects. Which do You Prefer when Teaching Solid Geometry? " - from the section: New Trends in Mathematical Education Solid geometry is an essential part of mathematics education. At present, there are various ways how to teach, learn and understand it. The purpose of this paper is to provide findings from our pedagogical research designed to analyse solutions of students and their teacher from a non-standard spatial visualisation problem. At the same time, we will point out at common characteristics among students’ solutions in relation to the group to which they were situated according to MPI. |
| VAJSÁBLOVÁ Margita " Geometry and Art on the Bohemiae Rosaand on Bleau’s Historical Maps in 17th Century " - from the section: Mathematics and Art Historical maps have not only factual but also artistic value. Their mathematical and geometric fundamental has great variability. The paper deals with geometric analysis of the projection on three maps of the 17th century mapping the world, Europe and Bohemia, whose authors are Willem Bleau with his son Joan. By analyzing the map curiosity of Bohemiae Rosa by Christoph Vetter, we showed the geometrical properties of its composition in conjunction with the author´s message. |
| VALLO Dušan " Geometry of Schwarz Lantern in GeoGebra " - from the section: New Trends in Mathematical Education The aim of this contribution is to bring some inspiration how to use dynamical geometry software Geogebra in teaching Mathematics and in teachers training education. For this purpose, we concerned with an example of the polyhedral surface titled as Schwarz lantern. We demonstrate the problem of numerical computing of its surface area via interactive graphics and spreadsheet environment. Some didactical remarks are included in the paper, too. |
| VANŽUROVÁ Alena " Homothety Curvature Homogeneous Riemannian Manifolds of Dimension Three " - from the section: Algebra and Geometry and Their Applications We distinguish here between curvature homogeneity (up to order r) and homothety curvature homogeneity (up to order r) of Riemannian manifolds with positive definite metric. Curvature homogeneous manifolds are Riemannian spaces whose curvature tensor is "the same" in all points (in some sense: in suitable, corresponding frames, components of curvature in two points are the same). For homothety curvature homogeneous spaces, curvatures (and their covariant derivatives) in two points are related in a more general way, namely "up to a multiple" which varries from point to point. Trivial examples of curvature homogeneous spaces are classical homogeneous spaces and connected locally homogeneous spaces. Our aim is to bring examples which are not locally homogeneous. We shall call them "non-trivial examples". We pay here attention to an interesting class of metrics in dimension three, which we call here "metrics of Sekigawa type" since first non-trivial examples were given by K. Sekigawa in 1970´th (and for a long time, only a few classes of such examples, that are not locally homogeneous, have been known). We give Sekigawa type examples which are homothety curvature homogeneous up to order one (and not more), but are not locally homogeneous. We show also that a generalisation of such Sekigawa-like metrics can be defined in arbitrary dimension. Under special assumptions, we can construct spaces of Sekigawa type, in any dimension, which are homothety curvature homogeneous and are not curvature homogeneous. |
| VARGA Marek " Notes to Indefinite Integrals " - from the section: New Trends in Mathematical Education We know convergent and divergent tasks in the didactics of mathematics. In divergent tasks there are several different ways lead to correct result. Could we to see problem “calculate indefinite integral” like divergent problem? In the article we will try to show different ways to finding primitive functions. |
| VARGOVÁ Michaela " Geometrical Perspective as the Introduction Into Limit Process " - from the section: New Trends in Mathematical Education The paper presents a geometrical approach for limit process of special sequences. Geometrical approach is very natural from historical point of view. Therefore, we decided to follow the parallel of phylogenesis and ontogenesis in mathematics in our educational process on university level mathematics course. |
| VASHPANOVA Nina " Special Deformations of Hypersurfaces of Riemannian Spaces " - from the section: Algebra and Geometry and Their Applications In the present paper we consider infinitesimal deformations of a pseudo-Riemannian space which map each geodesic to a curve approximating a geodesic with given precision. This approach seems to be more appropriate for applications than the standard one, for example, for simulating real physical situation when evolution of gravity fields, electromagnetic fields, mechanical systems is considered. |
| VELICHOVÁ Daniela " 1. Active Learning Methods in Engineering Mathematics - Adventure and Challenge 2. Interactive Learning Materials for Teaching Constructive Geometry Course " - from the section: New Trends in Mathematical Education 1. Paper brings information on experience with introduction of innovative active learning and teaching methods into basic course Mathematics I for the first year engineering students at the faculty of Mechanical Engineering, Slovak University of Technology in Bratislava, Slovakia. Evaluation of experiment results and students achievements is presented in statistical data. Supplementary analysis of feedback obtained from students in questionnaire shows insight into students opinions on various teaching scenarios and comparison of used methods of eduScrum and individual study. 2. Paper brings short information on development of dynamic instructional materials for basic course of Constructive geometry at the technical university. Some materials developed as GeoGebra interactive applets and videos provided as on-line learning materials for self-study of students will be described. Few remarks on the impact to the improvements of spatial abilities and understanding of spatial relations for technical university students will be included, too. |
| VIGHI Paola " Abstract Art as Tool to Learn Mathematicssuggestions from a Van Doesburg’s Painting " - from the section: Mathematics and Art This paper focuses on the possible links between Mathematics and Art. It shows how to discover mathematical concepts in a painting and how use them to make a suitable observation of this artistic creation. In particular, it presents a reading ‘with mathematical eyes’ of a picture, titled “Arithmetic Composition I”, made by Theo van Doesburg. It provides an example of approach to a picture that can promote the need to use mathematical tools for investigating in depth an artistic composition. |
| VINTERE Anna " Development of the Ability to Deal Ith and Manage Mathematical Language and Tools in the Course Mathematics for Economists " - from the section: New Trends in Mathematical Education In this article, a short description of the course "Mathematics for economists" of Latvia University of Life Sciences and technologies is given, course learning outcomes are presented and, the contribution of the course to the development of mathematical competences is analysed, based on lecturers´ survey. The course "Mathematics for economists" study results are illustrated by the results of the student survey, which shows how confident students are about their mathematical competence and knowledge. |
| VISNYAI Tomáš " Remarks on the Determining Sets of Strongly Separately Continuous Functions on l^p, p≥1 " - from the section: Differential Equations, Dynamic Systems and Their Applications In this paper we provide a sufficient condition for the set E⊆l^p, p≥1 to be determined for the strongly separately continuous functions defined on l^p, p≥1. We give an example of nearly open and super dense sets in the metric space of sequences of real numbers l^p, p≥1. |
| VOLNY Petr " Geometrical Meaning of Derivatives in GeoGebra " - from the section: New Trends in Mathematical Education The aim of the paper is to present teaching procedure based on the 3D module in GeoGebra. We regularly use GeoGebra during education of mathematics at university level. We would like to show connection and cooperation between the teacher, students and GeoGebra. It could be interesting for teachers and their future methodology of teaching. We present the GeoGebra approach for one topic from the chapter "Differential Calculus of Functions Depending on Two Real Variables", especially explanation of the geometrical meaning of partial derivatives. |
| ZÁHONOVÁ Viera " Interactive Learning Materials for Teaching Constructive Geometry Course " - from the section: Paper brings short information on development of dynamic instructional materials for basic course of Constructive geometry at the technical university. Some materials developed as GeoGebra interactive applets and videos provided as on-line learning materials for self-study of students will be described. Few remarks on the impact to the improvements of spatial abilities and understanding of spatial relations for technical university students will be included, too. |
| ZAHRÁDKA Jaromír " The Merrifield-Simmons Index for the Linear Octagonal Chains " - from the section: Algebra and Geometry and Their Applications The Merrifield-Simmons index for a simple undirected graph is given by the number of subsets of such that no two vertices in are adjacent. This number is one of the most popular topological index in chemistry, which was firstly defined and called as the Fibonacci number of a graph. Octagonal chains are cata-condensed systems of octagons and represent a class of polycyclic conjugated hydrocarbons. In this contribution we obtain an exact formula for the Merrifield-Simmons index of linear octagonal chains. |
| ZAWIŚLAK Stan " Neronal Network Based Trainigof Virtual Drivers in Car Racing Game " - from the section: Mathematical Aspects of Network Science and Applications The present paper is dedicated to the car racing computer game. The game consists in generation of racing route, generation of cars pictograms and generation of learning ‘engine’ for every racer and animation of the races. The user establishes the number of cars, chooses the route as well as enters the parameters of learning procedure. Own software was prepared. The neuronal networks were tested via changing their characteristics e.g. number of hidden layers. The analyses of effectiveness are enclosed. |
| ŽDÍMALOVÁ Mária " Magic with Fractals " - from the section: Mathematics and Art In this contribution we focus on frcatals. We present basic backround and its connection with mathematics and nature, We present basic classifications of frcatlas. Finallz we discuss their applications into art, architecture, virtula world, design and fashion. |
| ZEITHAMER Tomáš R. " Space-Time Theory of Retail Gravitation in Economics of Sun-Earth Relationships " - from the section: Nothing This paper is dealing with space-time theory of retail gravitation in economics of Sun-Earth Relationships. The mathematical model for physical space-time with the field of retail gravitation is based on a four-dimensional differentiable manifold on which is defined a symmetric covariant second-order tensor field, i.e. metric tensor having Lorentzian signature. (Coauthor of the paper: prof. Ing. Jiří POSPÍŠIL, CSc., Czech Technical University, Prague, Czech Republic) |
| ŽÍDEK Arnošt " Tutorials in the Math Support Centre at the Technical University of Ostrava " - from the section: New Trends in Mathematical Education Math Support Centre (MSC hereinafter) was opened at the Technical University of Ostrava in October 2016. Within the two years of its existence it became a popular place of study for many students of our university. During the last semester more than 400 consultations took place in the MSC. In this paper we first present principles of education in the MSC. Next, we introduce our implementation of tutorials, review lessons differing both from lectures and seminars. |
| Number of registered papers: 183 | Last change: 07.03.2019 |
© Ústav matematiy a fyziky, Strojnícka fakulta STU v Bratislave